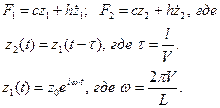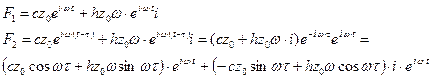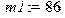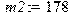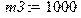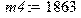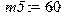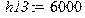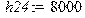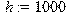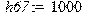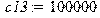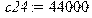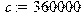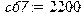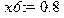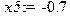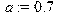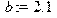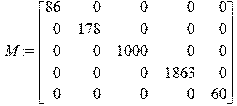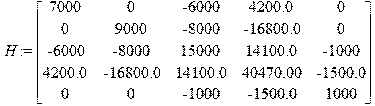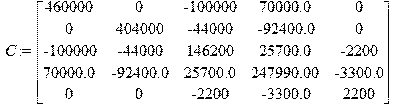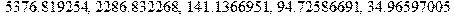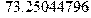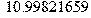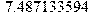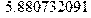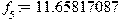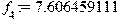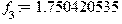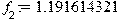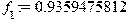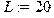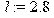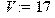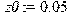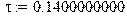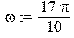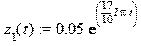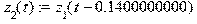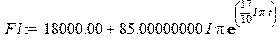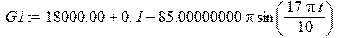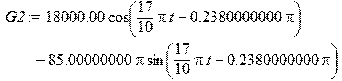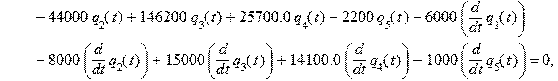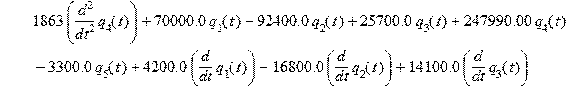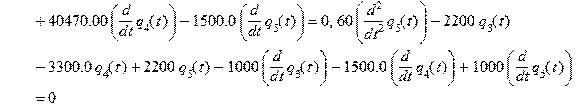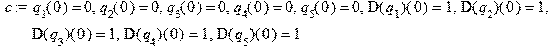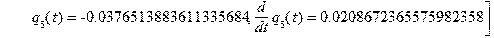|
|
Расчет собственных и вынужденных колебанийЛегкового автомобиля
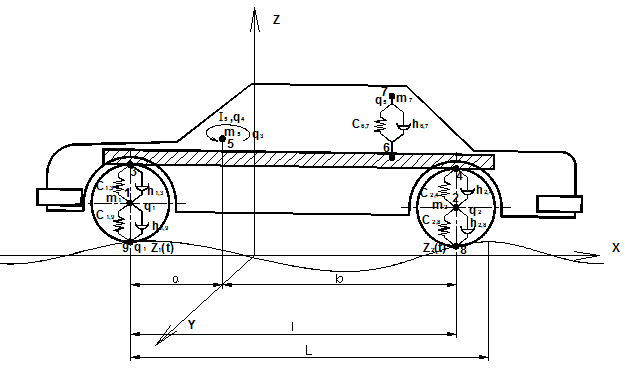
В настоящем разделе рассматривается математическая модель легкового автомобиля, полученная профессором кафедры прикладной математики Городецким Ю.И. и приведенная в его учебном пособии [8]. Рассмотрим, согласно [8], некоторые методические соображения по поводу математической модели, описывающей колебания легкового автомобиля. При построении математической модели предположим: 1) автомобиль совершает плоские колебания в плоскости xz. 2) профиль дороги имеет синусоидальный характер. 3) автомобиль движется равномерно со скоростью V(км/ч). 4) в автомобиле выделяется четыре колебательных элемента: а) кузов с силовым агрегатом б) передние колёса в) задние колёса и задний мост, которые считаются абсолютно жёсткими телами г) пассажир На рис. 3 приведена эквивалентная механическая модель, описывающая колебания легкового автомобиля в принятой идеализации.
Рис. 3. Блок-схема легкового автомобиля
На рисунке обозначено: 1) m1 – масса передних колёс, m2 – масса задних колёс и заднего моста, m5 – масса подрессоренной части автомобиля, m7 – масса человека 2) I5 – момент инерции подрессоренной части автомобиля относительно оси, проходящей через точку (5) и перпендикулярной плоскости (xz) 3) c1.3 – коэффициент жесткости передних рессор, с2.4 – коэффициент жесткости задних рессор, с – коэффициент жесткости шин колёс, с6.7 – коэффициент жесткости сиденья пассажира 4) h1.3 – коэффициент рассеивания энергии в передних амортизаторах, h2.4 – коэффициент рассеивания энергии в задних амортизаторах, h – коэффициент рассеивания энергии в шинах колёс, h6.7 – коэффициент рассеивания энергии в сиденье пассажира 5) l = a + b (расстояние между передними и задними колёсами автомобиля) a – расстояние от передних колёс до центра масс автомобиля b – расстояние от центра масс автомобиля до задних колёс 6) L – длина волны синусоидального профиля дороги 7) z1(t), z2(t) – величина профиля дороги в точках 9 и 8.
В качестве обобщённых координат взяты q1, q2, q3, q4, q5, характеризующие вертикальные колебания передних колёс, вертикальные колебания задних колёс и заднего моста, вертикальные, а так же угловые колебания кузова автомобиля и вертикальные колебания пассажира. При движении автомобиля по синусоидальному профилю дороги происходит взаимодействие между колёсами автомобиля и дорогой, которое необходимо учитывать при написании математической модели. Прежде всего, следует заметить, что задние колёса автомобиля набегают на профиль дороги величиной z2(t) = z1(t–τ), где z1(t) — величина профиля, на который набегают на передние колёса. При этом запаздывание τ = Теперь перейдём к построению математической модели. В основе построения лежат уравнения Лагранжа, которые имеют вид
где L = T–П — функция Лагранжа, Т и П — кинетическая и потенциальная энергии, B — диссипативная функция Релея,
Запишем выражение кинетической энергии
Потенциальная энергия представляет собой работу упругих сил на относительном перемещении ∆ij, являющихся функциями обобщённых координат.
Диссипативная функция Релея по своей структуре напоминает выражение потенциальной энергии, записанной относительно скоростей
где
Воспользуемся уравнениями Лагранжа второго рода и запишем математическую модель, описывающую колебания автомобиля:
В матричной форме записи математическая модель имеет вид:
Структура матрицы Н идентична структуре матрицы С. Также видно, что матрицы М, Н и С являются симметричными, причем,
Силы
Окончательное выражение для сил можно записать в следующем виде:
Построенная математическая модель позволяет выполнять различные расчёты, связанные со свободными и вынужденными колебаниями автомобиля. Для расчёта собственных частот и собственных форм колебаний необходимо использовать консервативную модель, положив в общих уравнениях матрицу диссипации и вектор внешних сил равными нулю. Для расчета переходных процессов следует в общем уравнении положить вектор внешних сил равным нулю и задать начальное смещение и начальные скорости рассматриваемой системы. Для расчёта вынужденных колебаний необходимо использовать общую математическую модель, считая вектор внешних сил периодической функцией. Таким образом, построенная математическая модель является достаточно универсальным инструментом в решении поставленной задачи об улучшения показателей динамического качества легкового автомобиля. Разработанный алгоритм и комплекс программ предназначены для расчёта собственных и вынужденных колебаний легкового автомобиля. В основу алгоритма и комплекса программ положена математическая модель, полученная в (2.2.1)–(2.2.8) и описывающая свободные и вынужденные колебания элементов расчётной схемы автомобиля и колебаний пассажира. В соответствии с расчётной схемой и математической моделью входными параметрами являются: инерционные параметры легкового автомобиля типа ГАЗ–3111 (массы передних колёс, заднего моста с колёсами, масса и момент инерции подрессоренной части автомобиля и масса пассажира); параметры жесткости и рассеивания энергии в элементах передней и задней подвесок. К входным параметрам можно так же отнести параметры сил, действующих на передние и задние колёса со стороны дороги (жесткость и рассеивание энергии в шинах, расстояние между осями передних и задних колёс, скорость автомобиля и длина волны профиля дороги).
Комплекс программ для расчета показателей динамического качества легкового автомобиля Расчет собственных частот и форм колебаний: > restart; > with(linalg):with(DEtools): Задание входных параметров: Массы элементов расчетной схемы автомобиля: [кг] > m1:=86;m2:=178;m3:=1000;m4:=1863;m5:=60;
Коэффициенты трения:[Hc/м] > h13:=6000;h24:=8000;h:=1000;h67:=1000;
> Коэффициенты жесткости в соединениях :[H/м] > c13:=100000;c24:=44000;c:=360000;c67:=2200;
Координаты точек расчетной схемы автомобиля:[м] > x6:=0.8;
> x5:=-0.7;
> a:=0.7; #расстояние от передних колес до центра масс автомобиля;
> b:=2.1; #расстояние от задних колес до центра масс автомобиля;
Матрица масс: > M:=matrix([[m1,0,0,0,0],[0,m2,0,0,0],[0,0,m3,0,0],[0,0,0,m4,0],[0,0,0,0,m5]]);
Матрица диссипации: > H:=matrix([[h13+1000,0,-h13,h13*a,0],[0,h24+1000,-h24,-h24*b,0],[-h13,-h24,h13+h24+h67,-h13*a+h24*b+h67*(x6-x5),-h67],[h13*a,-h24*b,-h13*a+h24*b+h67*(x6-x5),h13*a^2+h24*b^2+h67*(x6-x5)^2,-h67*(x6-x5)],[0,0,-h67,-h67*(x6-x5),h67]]);
Матрица жесткостей: > C:=matrix([[c13+360000,0,-c13,c13*a,0],[0,c24+360000,-c24,-c24*b,0],[-c13,-c24,c13+c24+c67,-c13*a+c24*b+c67*(x6-x5),-c67],[c13*a,-c24*b,-c13*a+c24*b+c67*(x6-x5),c13*a^2+c24*b^2+c67*(x6-x5)^2,-c67*(x6-x5)],[0,0,-c67,-c67*(x6-x5),c67]]);
Проверка матриц на положительную определенность: > definite(M,'positive_def');
> definite(H,'positive_def');
> definite(C,'positive_def');
Расчет обратной матрицы: > L:=evalm(1/M);
Перемножение матриц: > G:=evalm(L&*C);
Нахождение собственных чисел: > eigenvalues(G);
Нахождение собственных векторов: > eigenvectors(G);
Нахождение собственных частот: > sqrt(5365.628126);sqrt(2284.150981);sqrt(120.9607681);sqrt(56.05716945);sqrt(34.58300993);
Перевод частоты в Герцах: > f[5]:=evalf(73.25044796/(2*Pi));f[4]:=evalf(47.79279214/(2*Pi));f[3]:=evalf(10.99821659/(2*Pi));f[2]:=evalf(7.487133594/(2*Pi));f[1]:=evalf(5.880732091/(2*Pi));
Расчет вынужденных колебаний: Параметры, характеризующие дорогу: > L:=20; #длина волны синусоидального профиля дороги[м];
> l:=2.8; #расстояние между передними и задними колесами автомобиля[м];
> V:=17; #скорость движения автомобиля[м/с] ;
> z0:=0.05; #высота неровности дороги[м];
Коэффициент запаздывания: > tau:=l/L;
Частота с которой силы действуют на колеса при движении автомобиля: > omega:=(2*Pi*V)/L;
Профиль на который набегают передние колеса: > z[1](t):=z0*exp(I*omega*t);
Профиль, на который набегают задние колеса: > z[2](t):=z[1](t-tau);
Сила действующая на переднее колесо со стороны дороги:[H] > F1,F2::complex: > F1:=c*z0+h*z0*omega*I*exp(I*omega*t);
> G1:=evalc(Re(F1));
Сила действующая на заднее колесо со стороны дороги:[H] > F2:=c*z0*exp(I*omega*(t-tau))+h*z0*omega*I*exp(I*omega*(t-tau));
> G2:=evalc(Re(F2));
Математическая модель — система обыкновенных дифференциальных уравнений десятого порядка : > sys:=m1*diff(diff(q[1](t),t),t)+(c13+c)*q[1](t)-c13*q[3](t)+c13*a*q[4](t)+(h13+h)*diff(q[1](t),t)-h13*diff(q[3](t),t)+h13*a*diff(q[4](t),t)=G1, m2*diff(diff(q[2](t),t),t)+(c24+c)*q[2](t)-c24*q[3](t)-c24*b*q[4](t)+(h24+h)*diff(q[2](t),t)-h24*diff(q[3](t),t)-h24*b*diff(q[4](t),t)=G2, m3*diff(diff(q[3](t),t),t)-c13*q[1](t)-c24*q[2](t)+(c13+c24+c67)*q[3](t)+(-c13*a+c24*b+c67*(x6-x5))*q[4](t)-c67*q[5](t)-h13*diff(q[1](t),t)-h24*diff(q[2](t),t)+(h13+h24+h67)*diff(q[3](t),t)+(-h13*a+h24*b+h67*(x6-x5))*diff(q[4](t),t)-h67*diff(q[5](t),t)=0, m4*diff(diff(q[4](t),t),t)+c13*a*q[1](t)-c24*b*q[2](t)+(-c13*a+c24*b+c67*(x6-x5))*q[3](t)+(c13*a^2+c24*b^2+c67*(x6-x5)^2)*q[4](t)-c67*(x6-x5)*q[5](t)+h13*a*diff(q[1](t),t)-h24*b*diff(q[2](t),t)+(-h13*a+h24*b+h67*(x6-x5))*diff(q[3](t),t)+(h13*a^2+h24*b^2+h67*(x6-x5)^2)*diff(q[4](t),t)-h67*(x6-x5)*diff(q[5](t),t)=0, m5*diff(diff(q[5](t),t),t)-c67*q[3](t)-c67*(x6-x5)*q[4](t)+c67*q[5](t)-h67*diff(q[3](t),t)-h67*(x6-x5)*diff(q[4](t),t)+h67*diff(q[5](t),t)=0;
Начальные условия: > c:=q[1](0)=0,q[2](0)=0,q[3](0)=0,q[4](0)=0,q[5](0)=0,D(q[1])(0)=1,D(q[2])(0)=1,D(q[3])(0)=1,D(q[4])(0)=1,D(q[5])(0)=1;
Список функций – обобщенных координат:
> fcns:={q[1](t),q[2](t),q[3](t),q[4](t),q[5](t)};
Решение системы уравнений:
Ø F:=dsolve({sys,c},fcns,numeric); Ø
> F(2); > Построение графиков решений:
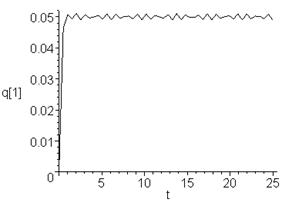
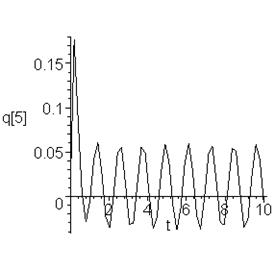
> plots[odeplot](F,[t,q[1](t)],0..25,color=blue);
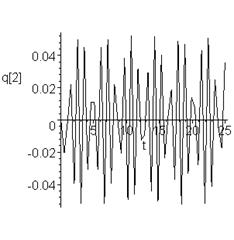
> plots[odeplot](F,[t,q[2](t)],0..25,color=orange);
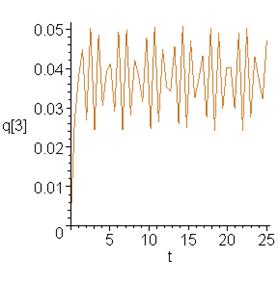
> plots[odeplot](F,[t,q[3](t)],0..25,color=gold);
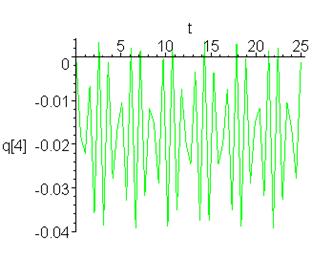
> plots[odeplot](F,[t,q[4](t)],0..25,color=green);
> plots[odeplot](F,[t,q[5](t)],0..10,color=violet);

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
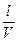 . Отметим также, что при движении автомобиля на его колёса действуют силы с частотой ω, которая определяется скоростью автомобиля и длиной профиля дороги ω =
. Отметим также, что при движении автомобиля на его колёса действуют силы с частотой ω, которая определяется скоростью автомобиля и длиной профиля дороги ω = 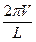 .
. (2.2.1)
(2.2.1) — вектор внешних сил.
— вектор внешних сил. . (2.2.2)
. (2.2.2)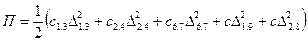 (2.2.3)
(2.2.3) , (2.2.4)
, (2.2.4)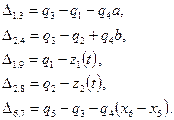 (2.2.5)
(2.2.5)
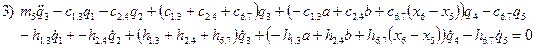
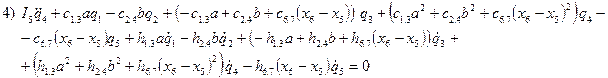
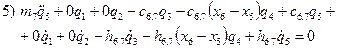

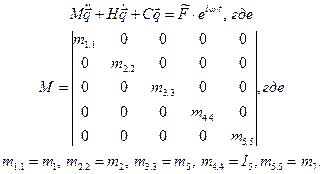 (2.2.6)
(2.2.6)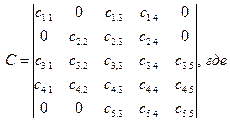
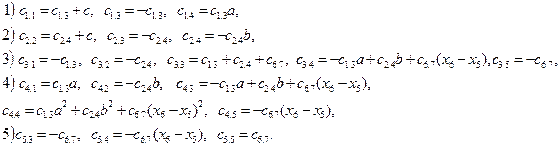 (2.2.7)
(2.2.7)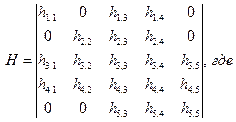
 (2.2.8)
(2.2.8) имеет следующий вид:
имеет следующий вид: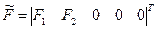
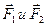 , действующие на колёса автомобиля со стороны дороги, определяются деформациями шины, которые зависят от амплитуды колебания колёс и профиля дороги
, действующие на колёса автомобиля со стороны дороги, определяются деформациями шины, которые зависят от амплитуды колебания колёс и профиля дороги