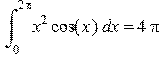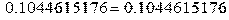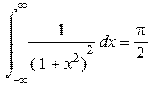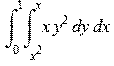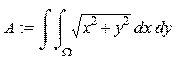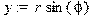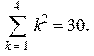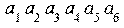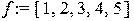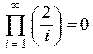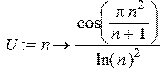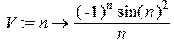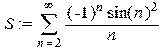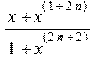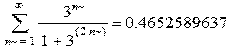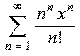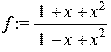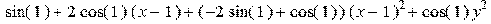|
|
Warning, the name changecoords has been redefined
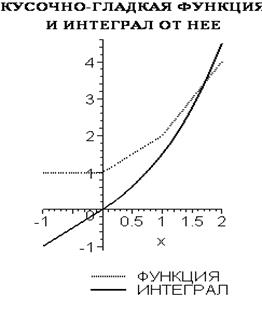
> f:=(x)->piecewise(x<0,1,x<=1,x+1,2*x);
> f(x);
> F:=x->int(f(x),x);
> F(x);
Ø plot([f(x),F(x)],x=-1..2,color=[RED,NAVY],linestyle=[DOT,SOLID],thickness=2,title="КУСОЧНО-ГЛАДКАЯ ФУНКЦИЯ \n И ИНТЕГРАЛ ОТ НЕЕ",titlefont=[TIMES,BOLD,9],legend=["ФУНКЦИЯ","ИНТЕГРАЛ"]);
Вычисление определенных интегралов: > restart: > Int(x^2*cos(x),x=0..2*Pi)=int(x^2*cos(x),x=0..2*Pi);
> Int(1/((x^3+x^2+2*x+2)^2),x=0..1)=int(1/((x^3+x^2+2*x+2)^2),x=0..1); evalf(%);
> # Интеграл с параметром; > s:=m->int(sin(x)^m,x=0..Pi/2);
> assume(m::integer>0); # Полагаем m>0 -целое; > s(m); # Г(x) - гамма-функция Эйлера;
Вычисление несобственных интегралов:
> restart: with(plots): > y:=(x)->(x*ln(x))/(1+x^2)^2;
> Int(y(x),x=0..infinity)=int(y(x),x=0..infinity);
> evalf(%);
Ø plot(y(x),x=0..infinity,title="ГРАФИК ФУНКЦИИ y(x)",titlefont=[HELVETICA,BOLD,10],thickness=3);
> Int(1/(x^2+1)^2,x=-infinity..infinity)=int(1/(x^2+1)^2,x=-infinity..infinity);
Вычисление двойных интегралов:
> restart: with(student): > Doubleint(x*y^2,y=x^2..x,x=0..1); # Внимание !! Порядок задания пределов интегрирования именно такой;
> value(%);
> Int(Int(x*y*(x+y),y=0..x^3),x=0..2)=int(int(x*y*(x+y),y=0..x^3),x=0..2);
> Int(Int(1/(x^2+y^2+5)^2,y=0..infinity),x=0..infinity);
> value(%);
Вычисление двойных интегралов путем перехода к полярным координатам:
> restart: with(student): > A:=Doubleint(sqrt(x^2+y^2),x,y,Omega);
> # При переходе к полярным используем r и phi; > assume(r>0); # полагаем r>o; > changevar({x=r*cos(phi),y=r*sin(phi)},A,[r,phi]);# заменяем переменные;
> # задаем область Omega; > Omega:=x^2+y^2<=a^2; x:=r*cos(phi);y:=r*sin(phi); Omega;#Область Omega в полярных координатах;
> simplify(%);
> Int(Int(r^2,r=0..a),phi=0..2*Pi); value(%);
Вычисление тройных интегралов:
> restart: with(student): with(plots): > Tripleint(x*y^2*z^3,x,y,z,V);
> # Интеграл ограничен поверхностями z=xy,y=x,x=1,z=0; > plot3d(x*y,x=0..1,y=0..1-x,axes=boxed);
> Tripleint(x*y^2*z^3,z=0..x*y,y=0..x,x=0..1); value(%);
> Int(Int(Int(exp(-x^2-y^2-z^2),x=-infinity..infinity),y=-infinity..infinity),z=-infinity..infinity)=int(int(int(exp(-x^2-y^2-z^2),x=-infinity..infinity),y=-infinity..infinity),z=-infinity..infinity);
> a(x,y,z):=1/(1+x+y+z)^(7/2);
Вычисление тройных интегралов через цилиндрические координаты: > restart: with(student): with(plots): > Tripleint(sqrt(x^2+y^2),x,y,z,V);
Ø implicitplot3d(x^2+y^2=z^2,x=-1..1,y=-1..1,z=0..1,grid=[15,15,15],axes=boxed);# Область V;
> # implicitplot3d -используется для отображения заданных в неявном виде поверхностей, а опция grid задает число базовых точек по которым строится поверхность (по умолчанию rid=[10,10,10]; > Tripleint(sqrt(x^2+y^2),x,y,z,V)=Int(Int(Int(sqrt(x^2+y^2),x=-sqrt(z^2-y^2)..sqrt(z^2-y^2)),y=-z..z),z=0..1);
> changevar({x=r*cos(phi),y=r*sin(phi)},Ihs(%),[r,phi,z]);
> # Определяем границу области интегрирования; > x:=r*cos(phi);
> y:=r*sin(phi);
> x^2+y^2=z^2;
> simplify(%);
> # Вычиcляем интеграл; > Int(Int(Int(r^2,r=0..z),phi=0..2*Pi),z=0..1):= int(int(int(r^2,r=0..z),phi=0..2*Pi),z=0..1);
1.6. Операции с рядами Применение систем символьной математики особенно эффективно при решении одной из задач математического анализа — операций с рядами. В настоящем разделе рассматриваются задачи анализа числовых и функциональных рядов, а также разложения функций в ряды Тейлора, Фурье, асимптотическое разложение. Числовые последовательности с заданным числом членов: > restart:with(plots): > sum(k^2,k=1..4);
> Sum(k^2,k=1..4)=evalf(sum(k^2,k=1..4));
> sum(k,k=1..n);
Бесконечные последовательности: > restart:sum(-exp(-k),k=1..n);
> sum(-exp(-k),k=1..infinity);
> Sum(k*a^k,k)=evalf(sum(k*a^k,k));
> Sum(1/n!,n=1..infinity)=evalf(sum(1/n!,n=1..infinity));
> Sum(n^2*exp(-sqrt(n)),n=1..5000)=evalf(sum(n^2*exp(-sqrt(n)),n=1..5000));
> Sum(n!/n^sqrt(n),n=1..1000)=evalf(sum(n!/n^sqrt(n),n=1..500));
Вычисление факториала числа: Ø 3!; Ø
> factorial(50);
Двойные суммы: > Sum(Sum(k^2,k=1..m),m=1..N);
> factor(simplify(value(%)));
> subs(N=100,%);
Вычисление произведений членов последовательности: > restart: > Product(k^2,k=1..5)=product(k^2,k=1..5);
> Product(k^2,k)=product(k^2,k);
> product(a[k],k=1..6);
> f:=[1,2,3,4,5]; product(f[k],k=1..5);
> product(n+k,k=1..4);
> Product(2/i,i=1..infinity)=product(2/i,i=1..infinity);
Общая схема исследования сходимости числовых рядов. Знакопостоянные ряды: > restart:with(linalg): > U:=(n)->(1/(ln(n)^2))*cos(Pi*n^2/(n+1));
> S:=Sum(U(n),n=2..infinity);
Проверка необходимого условия сходимости:
> Limit(U(n),n=infinity)=limit(U(n),n=infinity);
Для определения сходимости используем признак Даламбера:
> if limit(U(n+1)/U(n),n=infinity)<1 then print(R-сходится) else print (R- расходится) fi; R-расходится Знакопеременные ряды: > restart: > V:=(n)-> (-1)^n*sin(n)^2/n;
> S:=Sum(V(n),n=2..infinity);
Проверка необходимого условия сходимости: > Limit(V(n),n=infinity)=limit(V(n),n=infinity);
Построение графика частичных сумм ряда: > H:=(k)->sum((-1)^n*sin(n)^2/n,n=1..k);
> plot(H(k),k=1..400);
Построение графика частичных сумм ряда из модулей: > G:=(k)->abs(H(k));
> plot(G(k),k=1..400);
Нахождение суммы ряда:
> Sum((-1)^n*sin(n)^2/n,n=1..1000)=evalf(sum((-1)^n*sin(n)^2/n,n=1..1000));
Функциональные ряды:
> restart:with(plots): > U:=(x,n)->x^n/(1+x^(2*n));
> U(x,n+1)/U(x,n);simplify(%);
> Sum(U(x,n),n=1..infinity);
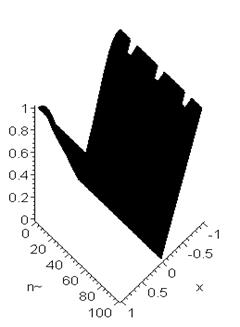
> assume(n>0); solve({abs(U(x,n+1)/U(x,n))<1.01},{x,n});
> f:=(x,n)->abs(U(x,n+1)/U(x,n));
> plot3d(f(x,n),x=-1..1,n=1..100,color=blue,thickness=2,axes=frame);
> x:=3; Sum(U(x,n),n=1..infinity)=evalf(sum(U(x,n),n=1..infinity));
> Степенные ряды :
> restart: > a:=(n)->(n^n)/(n!);
> Sum(a(n)*x^n,n=1..infinity);
> R:=limit(a(n)/a(n+1),n=infinity); evalf(%); # область сходимости -e^(-1) < x < e^(-1);
Разложение функций в ряд Тейлора: Функция от одного переменного:
> restart: with(plots):with(linalg): > # Разложение в ряд Тейлора до члена с x^4 функции f(x); > f:=(1+x+x^2)/(1-x+x^2);
> taylor(f,x=0);
> # Разложение в окрестности x=0 до порядка остатка = 5(необязательный параметр); > taylor(f,x=0,5);f1:=convert(%,polynom);f1;
> f1:=convert(%,polynom);# f1- основная часть ряда;
> # Сравним насколько отличается исходная функция от ее приближения рядом Тейлора; > plot([f,f1],x=-1..1.2,color=[BLUE,PINK],linestyle=[SOLID,DASHDOT],title="Функция и ее ряд Тейлора",titlefont=[HELVETICA,BOLD,10],legend=["функция","ряд Тейлора"],thickness=3);
Функция от двух переменных:
> restart: > mtaylor(f(x,y),[x,y],3): > mtaylor(sin(x^2+y^2),[x,y]);
> mtaylor(sin(x^2+y^2),[x,y],8);
> mtaylor(sin(x^2+y^2),[x,y],8,[2,1]);
> mtaylor(sin(x^2+y^2),[x=1,y],3);
Ассимптотическое разложение функций:
> restart:with(linalg): with(plots): 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|