
|
|
Математические методы обработки картографической информации.Математические методы применяются для выявления на картах и получения скрытой от непосредственного восприятия и недоступной для измерений и простых методов информации: пространственных закономерностей и особенностей, составляющих пространственных структур (подструктур), сложных интегральных пространственных структур, разнообразных структурных показателей. Применяемые в картопользовании математические методы можно объединить в четыре группы по специализации на типах пространственных структур, а внутри каждой группы разделить на две подгруппы по специализации на анализе и синтезе структур. На географических картах, как известно, встречаются четыре основных типа пространственных структур: поверхности, контурные или площадные, линейные и точечные. В процессе обработки этих структур математическими методами могут выполняться две противоположные по своей сущности операции – анализ и синтез. При выполнении анализа исходная структура на карте либо расчленяется на несколько более простых структур (аналитических карт), либо из нее извлекается требуемая подструктура (производная карта), либо получаются отдельные структурные показатели. При выполнении синтеза две или более исходных пространственных структур соединяются в новую комплексную или обобщенную пространственную структуру (комплексную или обобщенную синтетическую карту), либо «свертываются» в один или несколько обобщенных структурных показателей. Аналитическая подгруппаметодов обработки поверхностейвключает в себя аппроксимацию данного типа структур алгебраическими многочленами, полиномами, сплайнами, а также сглаживание осреднением. В синтетическую подгруппу методов работы с данными структурами входят операции сложения (вычитания), умножения (деления), методы корреляционного анализа (определение пространственного распределения значений коэффициентов парной, ранговой и частной корреляции, корреляционного отношения), методы многофакторного (дисперсионного, компонентного и факторного) анализа, методы анаморфоза (преобразования физической поверхности в «реальную» (транспортную или экономическую) в зависимости от транспортной обеспеченности или экономической ценности территории). В аналитическую подгруппу средств обработки контурных структурвходят методы: оценки сложности структуры, территориальной группировки контуров, оценки топологического положения, оценки формы и ориентировки контуров. В подгруппу синтеза данного типа структур входят методы: сложения и вычитания структур, оценки связей (полихорическим и тетрахорическим показателями), оценки пространственного соответствия (информационными показателями энтропии и избыточности). Аналитическую подгруппу средств обработки линейных структурсоставляют методы: оценки топологических свойств сетей, оценки пропускной способности сетей, оценки густоты сетей. В подгруппу средств синтеза линейно-сетевых структур входят методы корреляционного анализа, территориальной группировки, прогноза развития. Точечные структуры на картах анализируются с помощью методов оценки густоты, оценки регулярности, определения ближайшего соседства. При синтезе этих структур применяют методы территориальной группировки, корреляционного анализа, прогноза развития. Ниже приводятся характеристики основных методов анализа и синтеза двух наиболее распространенных видов структур на географических картах: поверхностей и контурных. Анализ поверхностей на картах можно выполнять с помощью методов алгебраических многочленов и полиномов. Для этого поверхность Отыскание численных значений составляющих выполняется при условии минимума отклонений
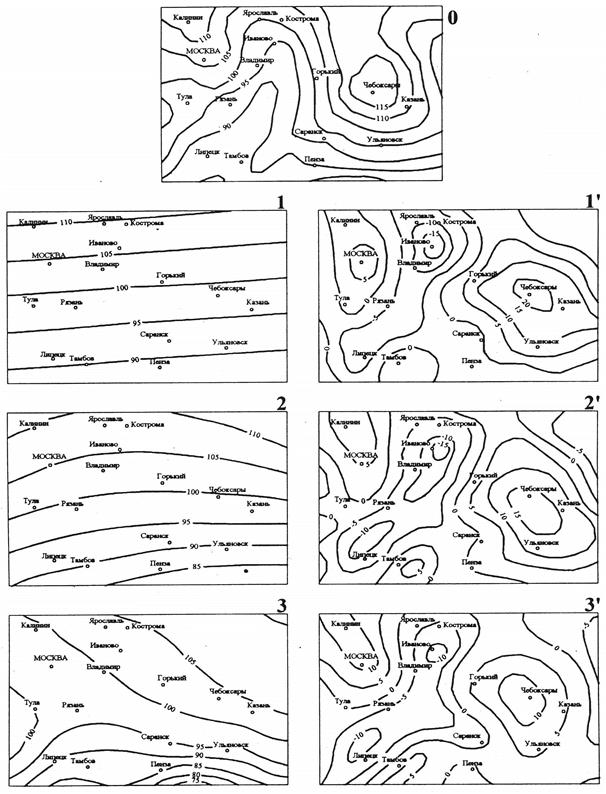
где m –число точек палетки, по которым определяются отклонения. При разложении Для вычислений А с карты снимают значения Поверхность на карте, аппроксимируемая: 1) многочленом первой степени будет представлена в первом приближении, плоскостью; 2) многочленом второй степени - во втором приближении, искривленной плоскостью; 3) многочленом третьей степени - более близкой к реальной поверхности, с меньшей, чем во втором приближении суммой квадратов отклонений, и т.д. до тех пор пока точность аппроксимирующей поверхности будет соответствовать требуемой величине. Ниже приведен пример разложения фрагмента карты урожайности картофеля (рис. 34,0) на составляющие поверхности (тренды) первой (рис. 34,1), второй (рис. 34,2) и третьей (рис. 35,3) степеней, а также на поверхности, отображающие распределение их отклонений от реальной поверхности (рис. 34,1’,2’,3’) . Разложение поверхностей методом полиномов отличается от рассмотренной тем, что аппроксимирующее уравнение выражается в виде независимых ортогональных многочленов
Если произведение
Первый коэффициент вычисляется по отдельной формуле: Точность аппроксимации методом полиномов оценивается формулой определения средних квадратических ошибок: Синтез поверхностей выполняется в основном с помощью корреляционных методов, в частности, метода парной корреляции, метода частной корреляции, метода множественной корреляции и метода корреляционного отношения. Первый метод применяется для оценки тесноты связи между поверхностями, отображающими распределение двух показателей А и В на одной территории, если связь между ними прямолинейная, с помощью коэффициента rab. Для установления формы связи между поверхностями и выполнения всех необходимых вычислений с обеих карт с помощью квадратной палетки снимают значения сопоставляемых показателей: ai и bi. После этого по значениям показателей строится график, на котором точки, отражающие связь между ними, могут распределиться: а) узкой полосой, которую можно аппроксимировать прямой линией; б) узкой полосой, аппроксимируемой кривой линией; в) в виде «облака», указывающего на отсутствие связи.
Рис 34 Если точки на графике распределились как в первом случае, то далее определяется коэффициент rab по формуле :
Значение средней квадратической ошибки rab определяется по формуле:
После вычисления коэффициента rab составляется уравнение регрессии:
Посредством вычитания из поверхности В поверхности Ниже приведен пример синтеза фрагментов карты плотности застройки городских земель (рис. 35,а) и карты удаленности земель от центра города (рис. 35,б). На основе вычислений коэффициента r, оценивающего зависимость показателя плотности застройки (
Рис 35 Метод частной корреляции применяется для определения влияния показателя С на связь между показателями А и В с помощью коэффициента rab/c, который вычисляется по формуле :
С его помощью можно, например, установить степень влияния на зависимость плотности городской застройки от удаленности показателя транспортной доступности земель. Метод множественной корреляции используется для оценки связи между показателем А и совокупностью показателей ( В,С,D…..L ).Формула оценивающего связь коэффициента основана на коэффициентах парной корреляции. Метод корреляционного отношения применяется в том случае, если корреляционный график, о котором говорилось выше, имеет криволинейную форму. Формулы вычисления коэффициента связи Анализ контурных структур на картах, составленных способами качественного фона и ареалов, может выполняться с помощью методов теории вероятностей и теории информации. Структуру этих карт можно, в частности, описать матрицами вероятностей совместных событий. Вероятность совместного события, 1. Ранжирование классов и отношений смежности между ними по значениям pii и pij с целью определения устойчивых попарных сочетаний в описанной в матрицах структуре. 2. Построение цепочек устойчивых сочетаний и представление их в виде графов. 3. Вычитание и осреднение матриц Px и Pу для определения асимметричности структуры, Кроме того, используя метод оценки энтропии матриц Px , Pу и Р, можно оценить степень структурной сложности анализируемой карты по формуле:
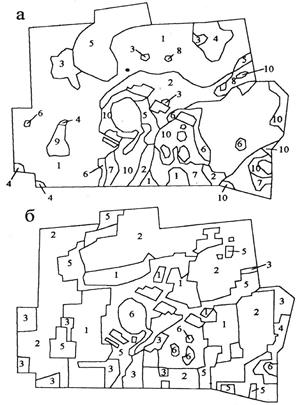
Пример применения матриц Px и Pу, некоторых операций с ними и оценки на их основе сложности контурной структуры карты показан ниже. Изображенный на рисунке 36,1 фрагмент карты земельных угодий имеет матрицы контурной структуры:
После их вычитания и осреднения получены матрицы:
Структурная сложность карты, оцененная энтропией по матрице Р, равна 2,206 (дв.единиц). Для сравнения структурная сложность генерализованного фрагмента, показанного на рисунке 36,2, оценивается значением 1,571 (дв.единиц). 1. 2.
Рис. 36 Синтез контурных структур можно выполнять с применением полихорического метода, тетрахорического метода и метода определения взаимного пространственного соответствия. Первый метод применяется для оценки тесноты связи показателем
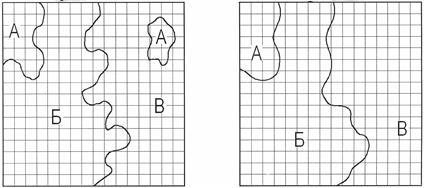
Тетрахорический метод применяется для оценки связи показателем S между картами А и В, составленными способом ареалов. При сопоставлении карт возможны четыре случая сочетания контуров: 1) а1 - контуры совпадают; 2) b1 - имеется контур карты А; 3) a2 - контуры отсутствуют; 4) b2 - имеется контур карты В. Вычисление показателя S выполняется по формуле: Наиболее эффективным из указанных методов при синтезе контурных структур является метод определения взаимного пространственного соответствия, формулы которого заимствованы из теории связи. Для оценки соответствия контурных структур двух карт используется показатель избыточности сообщения R, который вычисляется по формуле: Значения показателей энтропии определяются по расчетной матрице, в каждой клетке которой сверху вниз размещаются значения величин: nij-количество точек палетки, в которых сочетаются класс i карты А с классом j карты В; Ниже приводится пример сопоставления фрагментов карты агропроизводственной группировки почв (рис. 37,а) и карты использования земель (рис. 37,в). С помощью палетки и подсчетов nij; pij и pijlog2pij была получена матрица и суммарные значения этих величин по ее строкам и столбцам (см. табл. 7.1). Таблица 7.1.
Рис.37 Нижние величины в суммарной строке матрицы представляют собой значения pblog2pb; а нижние величины в суммарном столбце - значения palog2pa. Значение показателя избыточности в примере оказалось высоким (R= 0,86). Это безусловно указывает на то, что при организации использования земель на данной территории существенную роль играли агропроизводственные свойства почвенного покрова. Применение описанных математических методов обработки картографической информации, в силу большой трудоемкости, экономически оправдано только в условиях цифровых технологий. В этой связи необходимо заметить, что имеющиеся в составе многих ГИС функция оверлея применима для синтеза всех рассмотренных типов пространственных структур в любом их сочетании и потому оверлей можно отнести к универсальным методам синтеза картографической информации. ВОПРОСЫ ДЛЯ ПОГОТОВКИ К СДАЧЕ ЗАЧЕТА И ЗАЩИТЕ КУРСОВОЙ РАБОТЫ ПО ДИСЦИПЛИНЕ «ОБЩАЯ КАРТОГРАФИЯ». 1. Определение, краткая история развития и задачи картографии. 2. Разделы картографической науки и ее связи с другими дисциплинами. 3. Основные понятия: географическая карта, план, атлас, цифровая и электронная карта. 4. Структура (элементы) географической карты. 5. Классификации географических карт по масштабу, охвату территории и назначению. 6. Классификация географических карт по содержанию. 7. Картографические знаки: графические элементы и переменные; их применение. Понятие способа изображения информации на карте; названия основных способов и их графические переменные. 8. Способы изображения: значковый, количественного фона, картограммы, точечный. 9. Способы изображения: линейных знаков, качественного фона, картодиаграммы, изолиний. 10. Способы изображения: ареалов, локализованных диаграмм, линий движения, качественного фона. 11. Картографическая генерализация: определение, факторы, принципы и методы. 12. Приемы геометрической генерализации. 13. Основные понятия теории картографических проекций: картографическая проекция, географическая система координат и сетка, картографическая сетка, масштабы, искажения, эллипс искажений, изокола. 14. Классификации картографических проекций. 15. Частный масштаб длин: вывод формулы. 16. Вывод формулы масштаба площади. 17. Вывод формулы искажения углов. 18. Нормальные цилиндрические проекции (НЦП): общие формулы, свойства, применение 19. Вывод формулы 20. Формулы и сетка равноугольной НЦП. 21. Понятия локсодромии и ортодромии. 22. Вывод формулы 23. Формулы и сетка равновеликой НЦП. 24. Вывод формулы 25. Формулы и сетка равнопромежуточной НЦП. 26. Нормальные конические проекции (НКП): общие формулы, свойства, применение. 27. Вывод формулы 28. Формулы и сетка равноугольной НКП. 29. Вывод формулы 30. Формулы и сетка равновеликой НКП. 31. Вывод формулы 32. Формулы и сетка равнопромежуточной НКП. 33. Проекция РПЦ Гаусса-Крюгера: формулы и сетка. 34. Проекции, применяемые в отечественных топографических картах и планах: условия получения, формулы, свойства. 35. Нормальные азимутальные проекции (НАП): связь с НКП, общие формулы, свойства, применение. 36. Формулы и сетка равноугольной НАП. 37. Формулы и сетка равновеликой НАП. 38. Формулы и сетка равнопромежуточной НАП. 39. Перспективно-азимутальные проекции: виды, свойства и применение. 40. Виды картографических технологий создания карт. Этапы основных видов технологий. 41. Этап проектирования карты: последовательность и содержание работ; программа карты. 42. Этап составления карт: последовательность и содержание работ; способы переноса информации; авторский и составительский оригиналы карт. 43. Этап подготовки карты к изданию: цель и основные виды работ; печатные формы. 44. Этап издания карт: цель, принципы устройства и работы офсетных станка и машины, результат. 45. Особенности автоматизированного создания карт. 46. Способы и методы использования географических карт. Использование топографических карт и планов для инженерных изысканий. ЛЕБЕДЕВ Петр Петрович
ОБЩАЯ КАРТОГРАФИЯ
Пособие для изучения учебного курса студентами ВУЗ по специальности «Прикладная геодезия»
Компьютерная верстка текста и рисунков: Заляховская А.А.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
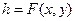 на географической карте необходимо представить аппроксимирующей ее функцией (трендом):
на географической карте необходимо представить аппроксимирующей ее функцией (трендом):  , где
, где  -аппроксимирующая функция, t - остаток аппроксимации. Далее
-аппроксимирующая функция, t - остаток аппроксимации. Далее  .
. :
: ,
, , где А - коэффициенты элементов разложения, которые необходимо определить.
, где А - коэффициенты элементов разложения, которые необходимо определить. ; c их помощью составляется система уравнений, которая решается по способу наименьших квадратов.
; c их помощью составляется система уравнений, которая решается по способу наименьших квадратов. и
и 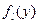 :
: , где
, где 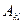 - коэффициенты, k и l- степень полинома (соответственно от 0 до n и от 0 до m).
- коэффициенты, k и l- степень полинома (соответственно от 0 до n и от 0 до m). обозначить
обозначить 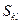 , то аппроксимирующее уравнение удет иметь вид системы:
, то аппроксимирующее уравнение удет иметь вид системы:  , решение которой по способу наименьших квадратов дает выражение для определения значений коэффициентов (кроме первого):
, решение которой по способу наименьших квадратов дает выражение для определения значений коэффициентов (кроме первого): .
. .
. .
.
 , где n – число снятых с карт пар значений
, где n – число снятых с карт пар значений  и
и  показателей А и В ; Ma и Mb - среднее арифметическое значение показателей А и В;
показателей А и В ; Ma и Mb - среднее арифметическое значение показателей А и В;  и
и  - среднее квадратическое отклонение значений показателей:
- среднее квадратическое отклонение значений показателей: ;
; 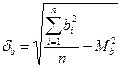 .
.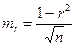 .
.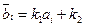 , где
, где 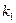 ,
,  - коэффициенты, определяемые по формулам
- коэффициенты, определяемые по формулам  ,
,  . С помощью полученного уравнения вычисляют значения показателя
. С помощью полученного уравнения вычисляют значения показателя  , которые отличаются от значений показателя В и зависят только от показателя А. Полученные значения
, которые отличаются от значений показателя В и зависят только от показателя А. Полученные значения 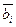 наносят на карту; по ним выполняется интерполяция и проводятся изолинии регрессионной поверхности
наносят на карту; по ним выполняется интерполяция и проводятся изолинии регрессионной поверхности  по территории в зависимости от показателя А.
по территории в зависимости от показателя А.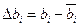 будет получена поверхность
будет получена поверхность  , которую называют остаточной поверхностью.
, которую называют остаточной поверхностью. ) от показателя удаленности (
) от показателя удаленности (  ), и значений показателя
), и значений показателя 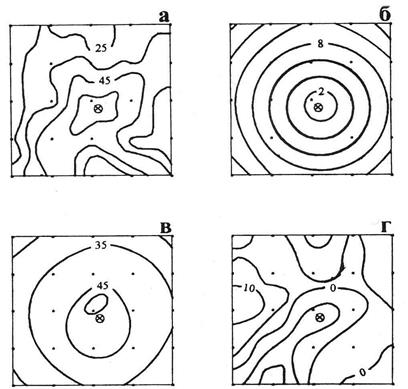
 , где rab, rac, rbc - коэффициенты парной корреляции.
, где rab, rac, rbc - коэффициенты парной корреляции. основаны на использовании матрицы частот значений показателей А и В и величин, получаемых в результате ее обработки.
основаны на использовании матрицы частот значений показателей А и В и величин, получаемых в результате ее обработки. , применительно к карте, если ее пространство, для удобства описания, представить дискретно в виде прямоугольной решетки с шагом
, применительно к карте, если ее пространство, для удобства описания, представить дискретно в виде прямоугольной решетки с шагом 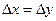 , насчитывающей n ячеек (точек) и вычисления выполнять раздельно по направлениям Х и У, - это доля пар смежных ячеек, занятых элементами i и j ее классификационной системы, состоящей из m классов, в общем количестве пар точек. Структура описывается двумя матрицами размером
, насчитывающей n ячеек (точек) и вычисления выполнять раздельно по направлениям Х и У, - это доля пар смежных ячеек, занятых элементами i и j ее классификационной системы, состоящей из m классов, в общем количестве пар точек. Структура описывается двумя матрицами размером  – Px и Pу, в диагональные клетки которых записываются доли сменных пар ячеек pii, принадлежащих одинаковым классам, и связывающих ячейки в контуры; другие элементы - доли пар ячеек pij, принадлежащих разным классам, и связывающих между собой соседние контуры. Матрица вероятностей является численным обобщением контурной структуры по одному из двух направлений, представляющая ее в суммарных относительных значениях: а) занимаемой каждым классом площади на карте; б) протяженности границ (смежности) между классами. Дальнейший анализ заключается в работе с матрицами Px и Pу с помощью следующих операций:
– Px и Pу, в диагональные клетки которых записываются доли сменных пар ячеек pii, принадлежащих одинаковым классам, и связывающих ячейки в контуры; другие элементы - доли пар ячеек pij, принадлежащих разным классам, и связывающих между собой соседние контуры. Матрица вероятностей является численным обобщением контурной структуры по одному из двух направлений, представляющая ее в суммарных относительных значениях: а) занимаемой каждым классом площади на карте; б) протяженности границ (смежности) между классами. Дальнейший анализ заключается в работе с матрицами Px и Pу с помощью следующих операций: и получения общей матрицы,
и получения общей матрицы, 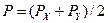 .
. .
.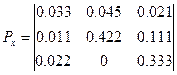 ;
; 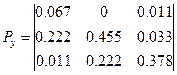
 ;
;  .
.
 , который вычисляется с использованием таблицы учета количества сочетаний классов признаков на сопоставляемых картах по формуле:
, который вычисляется с использованием таблицы учета количества сочетаний классов признаков на сопоставляемых картах по формуле: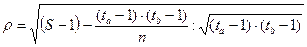 , где
, где ; p - частота точек в клетке ij учетной таблицы;
; p - частота точек в клетке ij учетной таблицы;  и
и  - частота встречаемости классов
- частота встречаемости классов  , соответствующие числу точек в столбце i и в строке j таблицы; n-общее число точек, по которым выполнялся учет количества сочетаний,
, соответствующие числу точек в столбце i и в строке j таблицы; n-общее число точек, по которым выполнялся учет количества сочетаний,  и
и  – количество классов в легендах карт.
– количество классов в легендах карт.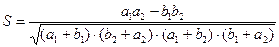 .
. , где Н - совместная энтропия структур обеих карт:
, где Н - совместная энтропия структур обеих карт:  ; Нmax-сумма энтропий обеих карт:
; Нmax-сумма энтропий обеих карт:  .
.
 равноугольной НЦП.
равноугольной НЦП. равноугольной НКП.
равноугольной НКП.