|
|
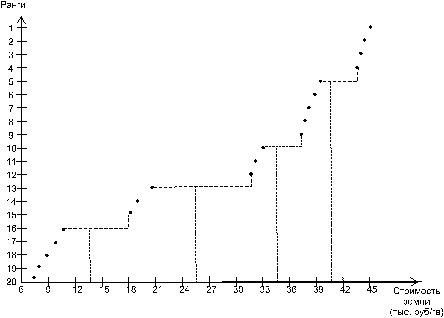
Легенда карты. Картографические шкалы.Легенда – неотъемлемая часть карты, которая включает в себя элементный состав ее информации, предоставленный в текстовом или числовом виде и обозначения состава, представленные в графическом виде. В легенде каждому элементу состава однозначно соответствует собственное графическое обозначение, поэтому она выполняет роль своеобразного ключа для формирования содержания карты. Если состав информации – качественные характеристики, то он, как правило, организован в легенде в виде классификационной системы; а если – количественные характеристики то – организован в виде числовой шкалы. Легенда, включающая в себя числовую шкалу, называется картографической шкалой. По характеру зависимости значений количественной характеристики и обозначающей ее графической переменной выделяют абсолютныеи условные картографические шкалы. Если они связаны между собой функциональной зависимостью, то такая шкала относится к абсолютным или пропорциональным, а если – нестрогой зависимостью, то – к условным или ранговым. К примеру, шкала, в которой количественная характеристика А обозначена размером (радиусом R) круговой диаграммы и зависимость между ними выражена формулой Числовые шкалы в структурном отношении бывают непрерывными, округленными и ступенчатыми. Ступенчатые числовые шкалы в свою очередь подразделяются на равноинтервальные, плавновозрастающие, плавноубывающие и произвольные. Ниже изложена методикаразработки ступенчатых шкал на примере данных стоимости земли (т. руб/га) для карты кадастровой оценки земельных участков. 1. По формуле 2. Проранжировать участки по значениям показателя в таблице (присвоить первый ранг участку, имеющему максимальное значение, второй ранг — следующему по значению участку и т. д., см. табл. 1); составить график «ранг-значение показателя» (рис. 32). Таблица 1
Рис. 32 По форме графика выбрать тип числовой шкалы: а) если точки распределились более или менее равномерно по прямой (или близко к ней) - равноинтервальная числовая шкала; б) если точки распределились более или менее равномерно по плавно вогнутой (или близко к ней) - шкала с постоянно возрастающим интервалом; в) если точки распределились более или менее равномерно по плавно выпуклой (или близко к ней) - шкала с постепенно убывающим интервалом; г) если точки распределились неравномерно (с разрывами и уплотнениями) - произвольная шкала.
3.Для получения равноинтервальной шкалы необходимо сначала определить интервал ступеней по формуле К Приведенный в таблице 1 и на рисунке 32 пример соответствует равноинтервальной шкале: 1) 6,3-12,8; 2) 12,9-19,3; 3) 19,4-25,8; 4) 25,9-32,3; 5) 32,4-38,8; 6) 38,9-45. 4. При получении шкалы с постепенно возрастающим интервалом необходимо учитывать степень прогиба графика. Если кривизна распределения точек - небольшая, следует выбрать вариант арифметической шкалы; если же кривизна - существенная, то - вариант геометрической шкалы. В первом случае сначала необходимо определить сумму всех номеров ступеней Если допустить, что данные таблицы 1 распределились на графике в виде плавной кривой с небольшим прогибом, тогда по этим формулам будут получены следующие значения К, D и Во втором случае при вычислениях границ ступеней используются десятичные логарифмы и антилогарифмы, а полученные с их помощью шкалы называют геометрическими. Сначала необходимо определить коэффициент по формуле Пример вычислений коэффициента K=(lg45-lg6,3):6=(l,6532-0,7784):6=0,1458 и нижних границ ступеней: 6) 1,6532-0,1458 = 1,5074; 101,5074= 32,17 = 31,2; 5) 1,5074-0,1458 = l,3616; 101,36I6= 22,99 = 23,0; В результате получена следующая геометрическая шкала: 1)6,3-8,4; 2) 8,4-11,7; 3) 11,8-16,3; 4) 16,4-22,9; 5) 23,0-32,1; 6) 32,2-45,0. 5. При получении шкалы с постепенно убывающим интервалом необходимо применять формулы аналогичные формулам для разработки постепенно возрастающих шкал, только определение границ необходимо начинать в первом случае с последней, а во втором случае с первой ступеней. Пример вычисления нижних границ убывающей арифметической шкалы: 6) 45-1-1,84 = 43,16 = 43,2; 5) 43,16-2-1,84 = 39,48 = 39,5; 4)39,48-3-1,84 = 33,96 = 34,0; 3) 33,96-4-1,84 = 26,60 = 26,6; 1) 17,40-6-1,84 = 6,3. На их основе построена следующая постепенно убывающая арифметическая шкала: 1) 6,3-17,3; 2) 17,4-26,5; 3) 26,6-33,9; 4) 34,0-39,4; 5) 39,5-43,1; 6) 43,2-45. 6. Определение границ ступеней произвольной шкалы выполняется непосредственно на графике, на котором разрывы делятся пополам, а полученные средние точки проецируются на ось показателя. Соответствующие им значения показателя принимаются за верхние границы ступеней
Рис. 33 Если количество таких естественных ступеней получилось меньше или больше n, то в первом случае наиболее крупные интервалы шаг за шагом разбиваются на 2 интервала до тех пор, пока их суммарное количество не станет равным значению n, а во втором случае попарно объединяются наиболее мелкие интервалы пока их сумма не станет равной n. В примере, приведенном на рисунке 33, разрывами образовано пять естественных ступеней: 1) 6,3-14,0; 2) 14,1-25,8; 3) 25,9-35,3; 4) 35,4-41,5; 5) 41,6-45,0. Чтобы получить шестиступенную шкалу, очевидно, первую степень, которая имеет небольшие значения границ ступеней, но сравнительно большой интервал (D1=7,7) и количество значений показателя (N1=5), следует разделить на 2 равные части и в итоге получить следующую шкалу: 1) 6,3-10,1; 2) 10,2-14,0; 3) 14,1-25,8; 4) 25,9-35,3; 5) 35,4-41,5; 6) 41,6-45,0. 7. Выполнить проверку правильности полученной тем или иным способом шкалы с помощью значений параметров Di и Ni (соответственно интервала ступени i и количества участков в ступени i ). При этом необходимо придерживаться следующих требований: а) распределение значений Di, по ступеням должно соответствовать логической структуре данной шкалы, а значения Ni от ступени к ступени для всех типов шкалы не должно изменяться б) в шкале не должно быть пустых ступеней, т.е. ступеней, в которых Ni =0. Шкалы, в которых эти правила не соблюдены, необходимо переделать или исправить. Например, если ошибочно при картировании данных, представленных в таблице 1 и на графике (рис. 32), была получена шкала с параметрами Di и Ni:
в которой не соблюдены правила равноинтервальности, равенства или плавности изменения Ni и недопустимости пустых ступеней, должна быть пересчитана заново, либо исправлена, например, таким образом, чтобы интервалы ступеней 1) и 3) были увеличены за счет уменьшения ступеней 2) и 4):

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
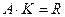 , где К – коэффициент пропорциональности шкалы, является абсолютной.
, где К – коэффициент пропорциональности шкалы, является абсолютной.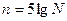 определить количество (целое число) ступеней (групп) шкалы, где N - количество земельных участков в таблице.
определить количество (целое число) ступеней (групп) шкалы, где N - количество земельных участков в таблице.
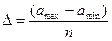 , где amax, аmin — максимальное и минимальное значения показателя; после чего аmin принять за нижнее значение первой ступени
, где amax, аmin — максимальное и минимальное значения показателя; после чего аmin принять за нижнее значение первой ступени 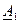 прибавит к нему интервал D и получить верхнюю границу первой ступени
прибавит к нему интервал D и получить верхнюю границу первой ступени  .
.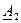 а, к
а, к 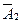 и. т. д., до тех пор, пока будут известны
и. т. д., до тех пор, пока будут известны 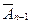 и
и 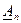 . За верхнюю границу последней степени
. За верхнюю границу последней степени 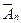 принять amax. Таким образом, ступени равноинтервальной числовой шкалы за исключением первой степени вычисляются по формулам:
принять amax. Таким образом, ступени равноинтервальной числовой шкалы за исключением первой степени вычисляются по формулам: 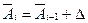 ,
,  .
.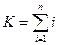 , общий интервал
, общий интервал 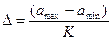 , а затем интервал для каждой ступени Di по формуле
, а затем интервал для каждой ступени Di по формуле 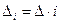 . После этого приступают к определению границ ступеней шкалы по формулам:
. После этого приступают к определению границ ступеней шкалы по формулам: 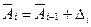 ,
,  ,
, 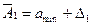 ,
, 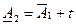 ,
, 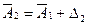 ; и. т. д.
; и. т. д.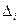 : К=1+2 + 3+4 + 5 + 6 = 21; D = (45,0-6,3) : 21 = 1,84;
: К=1+2 + 3+4 + 5 + 6 = 21; D = (45,0-6,3) : 21 = 1,84;  ;
; 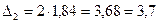 ;
; 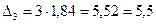 ;
; 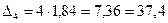 ;
; 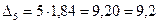 ; и числовая шкала:1) 6,3-8,1; 2) 8,2-11,8; 3) 11,9-17,2; 4) 17,3-24,4; 5) 24,5-33,4; 6) 33,5-45,0.
; и числовая шкала:1) 6,3-8,1; 2) 8,2-11,8; 3) 11,9-17,2; 4) 17,3-24,4; 5) 24,5-33,4; 6) 33,5-45,0.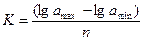 , а затем нижние границы шкалы по формуле
, а затем нижние границы шкалы по формуле 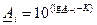 , начиная с последней ступени
, начиная с последней ступени 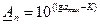 ;
; 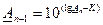 ;
; 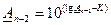 и. т. д., а так же верхние границы по формуле
и. т. д., а так же верхние границы по формуле 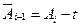 .
. , по которым определяют нижние границы соседних ступеней
, по которым определяют нижние границы соседних ступеней 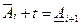 (рис. 33).
(рис. 33).