
|
|
Классификации картографических проекцийКартографические проекции можно классифицировать по различным признакам, главными из которых являются: вид нормальной сетки, характер (вид) искажений, положение полюса сферической системы координат. На основании первого признака все КП подразделяются на цилиндрические, коническиеи азимутальные проекции. Формулы цилиндрических проекций могут быть проиллюстрированы геометрически в виде цилиндра, описывающего эллипсоид и касающегося его поверхности по линии экватора или по линиям двух параллелей. Цилиндрические проекции образуют картографическую сетку прямоугольной формы (рис. 2а). Конические проекции иллюстрируются конусом, касающимся поверхности эллипсоида по линиям одной или двух параллелей; образуют сетку, меридианы которой – прямые линии, сходящиеся к точке плюса, а параллели – дуги концентрических окружностей с центром в точке полюса (рис. 2б). Азимутальные проекции иллюстрируются плоскостью, которая касается эллипсоида в точке полюса, и образуют сетку, параллели которой - концентрические окружности, а меридианы – прямые, пересекающиеся в точке полюса (рис. 2в). а) б) в)
Рис.2 На основании второго признака различают равноугольные, равновеликие и равнопромежуточные проекции. Равноугольные проекции не искажают углы, но существенно искажают площади; главным условием получения этих проекций является равенство частных масштабов по всем направлениям, в том числе по параллелям и меридианам, Равновеликие проекции не искажают площади, но существенно искажают углы. Главное условие этих проекций p=1 во всех точках карты. Равнопромежуточные проекции являются самым распространенным вариантом класса произвольных проекций; в них присутствуют все виды искажений, но их значения небольшие; главное условие этих проекций – m=1. Картографическая проекция, которая непосредственно отображает сетку географической системы координат, и образуемая ею картографическая сетка называются нормальными; в нормальных проекциях полюсы географической и сферической систем совпадают (
Рис.3
Формулы частного масштаба длин, масштаба площадей, искажения углов 1.а) б)
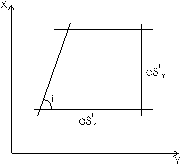
Рис.4 Из бесконечно малого сфероидического треугольника АА1А2 на рисунке 4а бесконечно малый отрезок После дифференцирования и замен получим развернутую формулу частного масштаба длин:
где e, f, g, – коэффициенты Гаусса, М – радиус кривизны меридиана, r- радиус параллели, a – азимут. Если a=0о(180о), то из данного выражения получается формула частного масштаба по меридиану 2. а) б)
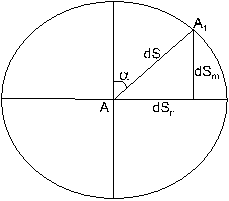
Рис. 5 Из рисунков 5а и 5б площадь бесконечно малой трапеции на эллипсоиде Для проекций с ортогональной сеткой 3. а) б)
Рис.6 Из бесконечно малых построенных относительно отрезков dS и dS’ прямоугольных треугольников на эллипсоиде и на карте (Рис.6):
После преобразования и подстановки получим: Поскольку
В проекциях с ортогональной сеткой 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



 .
. )Картографическая проекция, в которой используется полярная сферическая система координат с полюсом, расположенным относительно географической системы координат на ее экваторе (
)Картографическая проекция, в которой используется полярная сферическая система координат с полюсом, расположенным относительно географической системы координат на ее экваторе (  ), называется поперечной.Картографическая проекция, в которой используется система с полюсом, расположенным между географическим полюсом и экватором (
), называется поперечной.Картографическая проекция, в которой используется система с полюсом, расположенным между географическим полюсом и экватором ( 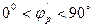 ), называется косой. Пример полярной сферической системы, используемой в косых проекциях, изображен на рисунке 3.
), называется косой. Пример полярной сферической системы, используемой в косых проекциях, изображен на рисунке 3.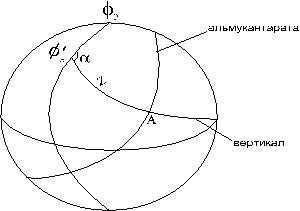

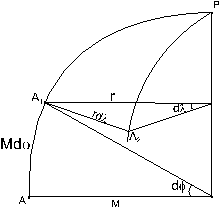
 ; из соответствующего ему плоского треугольника на карте
; из соответствующего ему плоского треугольника на карте  . Из треугольников на рисунках 4а и 4б
. Из треугольников на рисунках 4а и 4б  ,
, 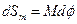 , где r – радиус параллели, а М – радиус кривизны меридиана. Подставив в общую формулу частного масштаба длин
, где r – радиус параллели, а М – радиус кривизны меридиана. Подставив в общую формулу частного масштаба длин  полученные выражения, имеем
полученные выражения, имеем  .
. (1),
(1),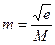 , а если a=90о(270о), то получится формула масштаба по параллели
, а если a=90о(270о), то получится формула масштаба по параллели  . Для шара
. Для шара  .
.
 , аплощадь соответствующей трапеции на карте
, аплощадь соответствующей трапеции на карте  . Подставив эти выражения в общую формулу масштаба площадей
. Подставив эти выражения в общую формулу масштаба площадей  , получим
, получим  . Зная, что отношения в скобках есть частные масштабы m и n, окончательная формула масштаба площадей получит вид:
. Зная, что отношения в скобках есть частные масштабы m и n, окончательная формула масштаба площадей получит вид:  (2).
(2). .
.
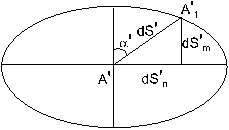
 ,
,  ;
;  ,
,  .
. ,
,  .
.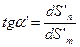 , то после замены dS’n и dS’m
, то после замены dS’n и dS’m  .Если правую и левую части выражения прибавить к tga и отнять от tga, тогда
.Если правую и левую части выражения прибавить к tga и отнять от tga, тогда  . Из школьной программы известно, что
. Из школьной программы известно, что  . После подстановки правого выражения в последнюю формулу имеем:
. После подстановки правого выражения в последнюю формулу имеем:  ,
,  . Разделив первую формулу на вторую, получим
. Разделив первую формулу на вторую, получим  . В этой формуле
. В этой формуле  , при
, при  и поскольку
и поскольку  , тогда
, тогда  .
. (3)
(3) .
.