|
|
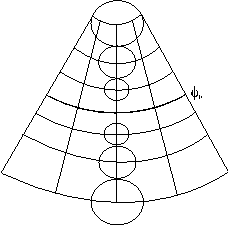
Общие формулы и свойства НКПКак следует из рисунка 13б, связь прямоугольных и полярных координат узловых точек картографической сетки в этой проекции выражается формулами:
Из рисунка 13б также следует, что Из рисунков 13в,г Значения искажений в данном классе проекций зависят только от Равноугольные НКП Формулу
Рис.14 1. Подставить в равенство вместо m и n их значения из общих формул, тогда 2. Написать формулу в интегральном виде: 3. Проинтегрировать, тогда Формулы равноугольных НКП
Равновеликие НКП Формулу 1. Подставить в последнее равенство значения m и n, получится 2. Записать в виде интеграла и его определить, тогда Формулы равновеликих НКП
Рис.15
Равнопромежуточные НКП Формулу 1.Подставить из общих формул НКП значение m, тогда 2. Проинтегрировать и получить Формулы равнопромежуточных НКП
Рис.16
Азимутальные проекции. Нормальные азимутальные проекции (НАП). а) б)
Рис.17 НАП являются частным случаем нормальных конических проекций, в которых параметр Перспективно-азимутальные проекции (ПАП).
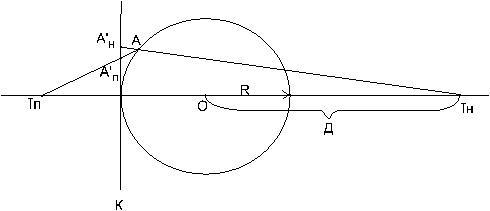
Рис.18 В ПАП поверхность земного шара с радиусом R проецируется по закону линейной перспективы на плоскость К из точки зрения Т. Если точка зрения находится перед плоскостью (Тп), то проекция образует позитивное изображение поверхности, а если за шаром (Тн)- негативное изображение. Последний вид проекций подразделяется на подвиды в зависимости от расстояния (Д) от точки Тн до центра шара, О: 1) Д=0 – гномонические; 2)Д=R –стереографические 3) R<Д<∞ - внешние; ;) Д=∞ -ортографические. Они показаны на рисунке 19 и обладают следующими свойствами.
2) В стереографической ПАП любая окружность изображается окружностью, поэтому ее применяют для карт звездного неба и графического решения по ним задач сферической астрономии.
3) Внешние ПАП используются для карт северного и южного полушарий Земли.
4) Ортографические ПАП хорошо передают сферичность, поэтому их применяют для картографирования планет.
Рис.19 3.7. Проекции, применяемые для топографических карт и планов. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,  , где q – расстояние между начальными точками координатных систем, r - радиус параллели, d - полярный угол.
, где q – расстояние между начальными точками координатных систем, r - радиус параллели, d - полярный угол. ,
,  , где a - параметр, который в конических проекциях меньше 1 и зависит от
, где a - параметр, который в конических проекциях меньше 1 и зависит от  (a=0 в НЦП, a=1 в азимутальных проекциях).
(a=0 в НЦП, a=1 в азимутальных проекциях). ;
;  .Искажение углов в НКП определяется по формуле
.Искажение углов в НКП определяется по формуле  .
.
 ;
;  .
. .
. ,
,  , где величина U зависит от
, где величина U зависит от  ,
,  ,
,  ,
,  .
.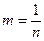 .
. , откуда
, откуда  .
. ,S – площадь сфероидической трапеции с разностью долгот в 1 радиан и протяженностью от экватора до текущей параллели; ее значение находится по
,S – площадь сфероидической трапеции с разностью долгот в 1 радиан и протяженностью от экватора до текущей параллели; ее значение находится по 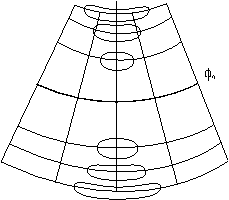
 ,
,  , p=1,
, p=1,  или
или 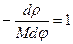 ,
, 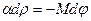 .
. , гдеs – длина дуги меридиана от экватора до текущей параллели; ее значение определяется по
, гдеs – длина дуги меридиана от экватора до текущей параллели; ее значение определяется по 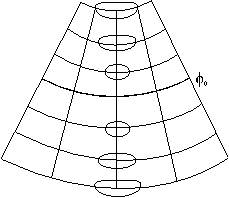
 ,
,  , m=1,
, m=1,  ,
,  .
.

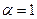 , поэтому их формулы выводятся аналогично формулам НКП с учетом данного условия. Поскольку в НАП искажения отсутствуют в точке полюса, то они применяются для картографирования полярных областей Арктики и Антарктики. Также как рассмотренные конические проекции НАП бывают равноугольные, равновеликие и равнопромежуточные с соответствующим для каждого вида распределением искажений.
, поэтому их формулы выводятся аналогично формулам НКП с учетом данного условия. Поскольку в НАП искажения отсутствуют в точке полюса, то они применяются для картографирования полярных областей Арктики и Антарктики. Также как рассмотренные конические проекции НАП бывают равноугольные, равновеликие и равнопромежуточные с соответствующим для каждого вида распределением искажений.