
|
|
Курсовой работы по курсу «Динамика конструкций» , включающей расчетные динамические модели образцов вооружения конкретных конструктивно-компоновочных схем
Курсовые работы студентов включают расчетные динамические модели объектов конкретных компоновочных схем с возмущениями и параметрами, задаваемыми для каждого варианта. Подобраны варианты заданий по математическому моделированию динамики систем как с двумя, тремя, так и более степенями свободы с учетом требований читаемого курса применительно к специальностям факультета — «Оружия и систем вооружения» (Е). Для студентов, желающих выполнить задания курсовой работы повышенной трудности, предлагаются варианты заданий по математическому моделированию динамики систем с 4, 5 степенями свободы. Расчетное задание позволяет студенту увязать изучение данной дисциплины с характером будущей инженерной деятельности. Для этого процесс решения задач доводится до решения уравнений и изучения характера движения системы с последующим анализом влияния параметров системы на ее движение. Программирование алгоритмов решения этих задач проводится студентами самостоятельно под руководством преподавателя. Последовательность действий при использовании уравнений Лагранжа второго рода для решения задач о движении голономных систем с несколькими степенями свободы указана в главе 2, 9.Изучение дисциплины заканчивается защитой курсовой работы с оценкой и экзаменом.
Пример 6.1. выполнения курсовой работы по динамике несвободной механической системы с двумя степенями свободы (рис.6. 2.1
Рис.6. 2.1. Полый цилиндр 2 массой m2 скользит по основанию 1 массой m1, способному вращаться вокруг неподвижного цилиндрического шарнира О. Основание удерживается спиральной пружиной с крутильной жесткостью Cj. В начальном положении механизм находится в состоянии статического равновесия и пружина деформирована. Введем неподвижную систему координат OXYZ, так, чтобы ось OX была горизонтальна, и связанную с основанием систему координат OX1Y1Z1, ее ось OX1 параллельна оси цилиндра и направляющим основания, по которым скользит цилиндр. Центр масс основания O1 в системе координат OX1Y1Z1 имеет координаты x1O и y1O. Начальное положение Oн центра масс цилиндра O2 определяется координатами x2O и y2O точки Oн в системе координат OX1Y1Z1. В начальный момент времени к внутренней поверхности дна цилиндра прикладывается нагрузка
где значения постоянных: P1 = 2, 37×106 H; a1 = 6,68×1010H / c 2 ; t1 = 0,005 c; P2 = 0 H; a2 = 0 H / c2; t2 = 0 c . При этом цилиндр 2 начинает двигаться по основанию 1, вызывая вращение последнего вокруг оси шарнира OZ. Движение цилиндра тормозится реакцией тормозного устройства 3, приложенной к внешней поверхности дна цилиндра:
где значения постоянных: R1 = 2,4×105 H ; b1 = 5,8×106H / c; t3 = 0,01 c ; R2 = 0 H; b2 = 0 H / c. Коэффициент трения скольжения при движении цилиндра по основанию f = 0,12. Моменты инерции основания 1 и цилиндра 2 относительно осей O1z1 и O2z2 равны J1 и J2, соответственно. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ. Указание. В качестве обобщенных координат выбрать угол поворота j основания 1, отсчитанный от горизонтали (в начальный момент j = j0) и координату S центра масс цилиндра 2 на направляющей основания 1, отсчитанную от его начального положения.
Решение.Система имеет 2 степени свободы k=s , в качестве обобщенных координат выбираем: 1) угол поворота j основания 1 вместе с цилиндром 2, отсчитанный от горизонтали (в начальный момент j = j0) ¾ q1=j; 2) и координату S движения центра масс цилиндра 2 на направляющей основания 1, отсчитанную от его начального положения ¾ q2=S. Таким образом, обобщенные координаты: q1=j, q2=S, обобщенные скорости: Запишем уравнения Лагранжа второго рода
Кинетическая энергия рассматриваемой механической системы относительно неподвижной системы отсчета: Т=Т1+Т2. Представим ее как функцию времени t, обобщенных координат q1=j, q2=S и обобщенных скоростей T = T (q1=j, q2=S ,
Кинетическая энергия основания 1, совершающего вращательное движение относительно оси OZ.
Кинетическая энергия цилиндра 2, совершающего плоско-параллельное движение относительно неподвижной системы отсчета
Формулы преобразования координат и поворотная матрица
¾ для центра масс основания 1
¾ для центра масс цилиндра 2
Матрица скоростей:
После приведения подобных членов относительно обобщенных скоростей, получаем T= T1+T2, а именно
Уравнения Лагранжа второго рода для данной системы имеют следующий вид:
Вычислим производные от кинетической энергии системы:
В левой части уравнений Лагранжа, как правило, оставляют слагаемые со вторыми производными от обобщенных координат. Все остальные переносятся в правую часть уравнения. Таким образом, обозначив слагаемое в последнем выражении как
окончательно получаем уравнение Лагранжа второго рода
Обобщенные силы для механических систем с числом степеней свободы i = s = 2
Для определения обобщенной силы
Определяя
Сравнивая множитель (в квадратных скобках) в выражении полученной виртуальной работы перед вариацией dS с формулой (5*), получаем выражение для второй обобщенной силы:
Составим дифференциальные уравнения в виде матриц:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 (6.1)
(6.1) (6.2)
(6.2)






 , а именно:
, а именно: .
.
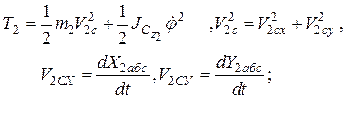
 относительно оси OZ в соответствии с формулами (3.18) и 3.19 главы 3 имеют вид:
относительно оси OZ в соответствии с формулами (3.18) и 3.19 главы 3 имеют вид:







 ;
;  .
.



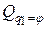 ,
,  , отвечающих выбранным обобщенным координатам, целесообразно вычислять последовательно, учитывая, что обобщенные координаты, а значит и их вариации независимы между собой. Системе всегда можно сообщить такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются. В этом случае из (2.27)главы 2 получаем:
, отвечающих выбранным обобщенным координатам, целесообразно вычислять последовательно, учитывая, что обобщенные координаты, а значит и их вариации независимы между собой. Системе всегда можно сообщить такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются. В этом случае из (2.27)главы 2 получаем: (5*)
(5*) и найдем виртуальную работу от всех заданных активных сил:
и найдем виртуальную работу от всех заданных активных сил:
 Сравнивая множитель (в квадратных скобках) в выражении виртуальной работы перед вариацией dj с формулой (5*), получаем выражение для первой обобщенной силы:
Сравнивая множитель (в квадратных скобках) в выражении виртуальной работы перед вариацией dj с формулой (5*), получаем выражение для первой обобщенной силы:
 , будем полагать, что ds ¹ 0, а для угла j поворота цилиндра (2),будем считать dj =0 (j=const), т.е.
, будем полагать, что ds ¹ 0, а для угла j поворота цилиндра (2),будем считать dj =0 (j=const), т.е.

