
|
|
Виртуальная работа силы. Идеальные связи
Виртуальной работой силы называется работа силы на любом виртуальном перемещении точки ее приложения: ¾ 1*)dА( Для вычисления виртуальной работы можно применять известные формулы для элементарной работы силы, подставляя вместо элементарного возможного При использовании декартовых координат ¾ 1**)dА( Например, виртуальная работа горизонтальной силы Fx = - F, xс = BC cosj и dxс= - BC sinj ×dj, то dА( Если к твердому телу, вращающемуся вокруг неподвижной оси l =Oz приложена сила ¾ 2*) dА( где dj ¾ виртуальный угол поворота тела вокруг оси l =Oz . ¾ 3*)dА( . где Ft - проекция силы на направление касательной, ds – вариация траекторной координаты точки приложения силы при траекторном способе задания ее движения. ¾4*)dА ( , где Fv - проекция силы на направление скорости точки приложения силы, dS – вариация перемещения точки приложения силы.
Виртуальная работа потенциальных сил изохронной вариации силового потенциала dА = dU или со знаком минус вариации потенциальной энергии системы dА = - dП.
Установив понятие виртуальной работы силы , можно расширить классификацию связей, разделяя их на идеальные и неидеальные. Связи называются идеальными , если равна нулю сумма виртуальных работ реакций этих связей на любом виртуальном перемещении системы ( из занимаемого в данный момент времени положения). Для идеальных связей или Полагая связи идеальными, можно решить задачу динамики несвободной системы. Эта задача состоит в том, что для данной системы с заданными активными силами и начальными условиями нужно найти уравнения движения и реакции связей. Например, если материальная точка движется по гладкой поверхности, уравнение которой f (x, y, z) = 0 , то нормальная реакция
Уравнения связи совместно с дифференциальными уравнениями движения точки образуют замкнутую систему уравнений. Эта система уравнений позволяет определить как уравнения движения точки, так и множитель Лагранжа, а значит, и нормальную реакцию связи
Примеры идеальных связей 1. Гладкая поверхность (плоскость)для материальной точки. В этом случае dА ( так как вектор
3. Цилиндрические и сферические шарниры, если поверхности соприкасающихся тел считаются идеально гладкими. Если твердое тело при помощи шарнира прикреплено к неподвижной опоре (рис.2.8), то реакция приложена к неподвижной Рис.2,8точке. Поэтому виртуальное перемещение такой точки равно нулю и dА ( 4. Твердая шероховатая поверхность для цилиндрического катка при качении без скольжения. Контакт катка с поверхностью происходит по линии. Поэтому реакцией связи является система сил, распределенных вдоль линии контакта. Виртуальная работа сил реакции равна нулю так как они приложены к неподвижным в каждый момент времени точкам ¾ СМЦС сечений катка (рис.2.1). Обобщенные силы В аналитической механике наряду с понятием о силе как векторной величине, характеризующей воздействие на данное тело со стороны других материальных тел, используют понятие об обобщенной силе. Для определения обобщенной силы рассмотрим виртуальную работу сил, приложенных к точкам системы.
Если механическая система при наложенных на нее голономных удерживающих h связях имеет s =3n-h степеней свободы, то положение этой системы определяется обобщенными координатами и (2.11):
Подставляя (2.14): (2.24), получаем
Скалярную величину называют обобщенной силой, соответствующей i-й обобщенной координате. Обобщенной силой, соответствующей i-й обобщенной координате, называется величина, равная множителю при вариации данной обобщенной координаты в выражении виртуальной работы сил, действующих на механическую систему. Виртуальная работа определяется от ¾ задаваемых активных сил, независящих от ограничений и ¾ реакций связей (если связи не идеальны, то для решения задачи необходимо дополнительно задать физическую зависимость Tj от Nj, (Tj ¾это, как правило, силы трения или моменты сопротивления трению качения, которые мы умеем определять). В общем случае обобщенная сила является функцией обобщенных координат, скоростей точек системы и времени. Из определения следует, что обобщенная сила ¾ скалярная величина, которая зависит от выбранных для данной механической системы обобщенных координат. Это значит, что при изменении набора обобщенных координат, определяющих положение данной системы, изменятся и обобщенные силы. Пример 2.10. ¾ либо q = s ¾ перемещение центра масс диска, ¾либо q = j ¾ угол поворота диска. Если пренебречь сопротивлением качению, то : ¾в первом случае обобщенной силой будет Рис. 2.9 Qs = mg sina, а ¾во втором случае ¾ Qj = mg r cosa. Обобщенная координата определяет и единицу измерения соответствующей обобщенной силы. Из выражения (2.25)
следует, что единица измерения обобщенной силы равна единице измерения работы, деленной на единицу измерения обобщенной координаты. Если в качестве обобщенной координаты q принять q = s ¾ перемещение какой-либо точки, то единица измерения обобщенной силы Qs ¾ будет[ньютон], Если же в качестве q = j ¾ будет принят угол поворота (в радианах) тела, то единицей измерения обобщенной силы Qj ¾ будет [ньютон ´ метр].

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ) =
) = 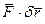 . (2.17)
. (2.17) виртуальное
виртуальное  перемещение точки.
перемещение точки. (2.22)
(2.22)
 f , где l ¾ неопределенный множитель Лагранжа [ ].
f , где l ¾ неопределенный множитель Лагранжа [ ]. (2.23)
(2.23) )=
)=  2. Нерастяжимая нить. Реакция нити ¾ сила ее натяжения ¾ ортогональна виртуальному перемещению точки ее приложения. Поэтому
2. Нерастяжимая нить. Реакция нити ¾ сила ее натяжения ¾ ортогональна виртуальному перемещению точки ее приложения. Поэтому  = 0 и др.
= 0 и др. (2.24)
(2.24) ( i = s )
( i = s ) Согласно (2.13), (2.14) виртуальное перемещение k – й точки
Согласно (2.13), (2.14) виртуальное перемещение k – й точки (2.13)
(2.13) (2.14)
(2.14) в формулу для виртуальной работы сил
в формулу для виртуальной работы сил
 (2.25)
(2.25) =
=  (2.26)
(2.26) Для диска радиусом r и массой m , который катится без скольжения по наклонной плоскости (рис.2.9), за обобщенную координату можно принять:
Для диска радиусом r и массой m , который катится без скольжения по наклонной плоскости (рис.2.9), за обобщенную координату можно принять: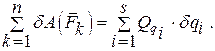 (2.27)
(2.27)