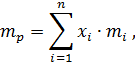Тема 7. Портфельный анализ

Методические указания.

Портфелем принято считать совокупность активов, собранных воедино для достижения инвестиционных целей вкладчика. В портфель могут входить акции, облигации, депозитные и сберегательные сертификаты и т.п.

Количество активов в портфеле обозначим через n.

Доходность портфеля рассчитывается как взвешенная средняя из ожидаемых доходов каждого актива:

где x_i – доля инвестиций, размещенных в активе i – го вида (портфельный вес актива); в векторной форме совокупность долей можно записать X^T = (x₁, x₂, …, x_n); m_i – ожидаемая ставка дохода актива i – го вида.

Риск портфеля определяется стандартным отклонением ставок доходности активов по портфелю:

или в скалярном виде

где σ_i – риск актива i – го вида; COV – ковариационная матрица порядка n; r_ij – коэффициент парной корреляции активов i – го и j – го видов.

Элементы ковариационной матрицы и коэффициенты парной корреляции активов определяются статистически по выборке ставок доходности активов на исследуемом интервале времени.Элементы ковариационной матрицы связаны с соответствующими коэффициентами парной корреляции формулой:

Изменяя структуру вектора Х, то есть перераспределяя объемы инвестиций между активами мы можем управлять показателями доходности и риска портфеля.

Пример 7.1. Портфель состоит из двух видов акции А и Б. Ожидаемая доходность акций А – 15%, акций Б – 8%. Стандартное отклонение акций А – 24%, акций Б – 9%. Коэффициент корреляции r₁₂ = - 0,8 . Построить линию эффективной границы портфеля.

Решение.

Долю инвестиций в акции А обозначим через Х₁, а долю инвестиций в акции Б обозначим через Х₂.

Структура портфеля должна удовлетворять условиям: Х₁ + Х₂ =1, Х₁ ,Х₂ ≥ 0.

Построение линии эффективной границы портфеля требует вычисления доходности и риска портфеля.

Доходность портфеля определяется выражением:

Риск портфеля рассчитывается по формуле:

Результат вычислений приведен в таблице:

Из расчетов видно, что доходности всех рассмотренных портфелей не выходят за пределы включенных в портфель активов, но риск портфеля может принимать значения меньшие, чем минимальный риск любого актива, входящего в портфель. Это становится возможным благодаря включению в портфель отрицательно коррелированных активов (r_ij < 0).

На рисунке качественно показаны изменения доходности и риска портфеля в зависимости от его структуры:

- Точке А соответствует портфель с номером 21, включающий только актив А.

- Точке Б соответствует портфель с номером 1, включающий только актив Б.

- Точке М соответствует портфель с номером 6, в котором доля актива А составляет 0.25, а доля актива Б составляет 0.75.

Из анализа графика также видно, что портфели, которым соответствуют структуры кривой МБ, при одинаковых рисках имеют доходности меньшие, чем портфели, расположенные на кривой МА. То есть портфели МА доминируют портфели МБ. Линию МА называют эффективной границей портфеля.

Следует отметить, что построение эффективной границы для портфеля из трех и более активов рассмотренным выше способом, затруднительно.

Пример 7.2.Сформировать портфель минимального риска из двух видов акции А и Б. Ожидаемая доходность акций А – 15%, акций Б – 8%. Стандартное отклонение акций А – 24%, акций Б – 9%. Коэффициент корреляции r₁₂ = - 0,8 . Доходность портфеля должна быть не ниже 10,8%.

Решение.МодельМарковица формулируется следующим образом:

найти вектор X = (x₁; x₂), минимизирующий риск портфеля σ_р , при m_p ≥ 10,8% .

Уравнения модели имеют вид:

при ограничениях

Решать оптимизационную задачу будем с использованием надстройки «Поиск решения» табличного процессора Excel, для чего разработаем шаблон, в который занесем уравнения модели.

Ячейки В2, С2 резервируются под искомые значения переменных х₁ и х₂ . Первоначально они пустые.

Ячейки В4, В5, В6, С5, С6 содержат параметры задачи.

В ячейке D8 вычисляется риск портфеля по формуле:

=(B2^2*B6^2+C2^2*C6^2+2*B6*C6*B4*B2*C2)^0,5

В ячейки В10, С10 копируются показатели доходности активов из строки 5. В ячейке D10 вычисляется левая часть первого ограничения по формуле:

=СУММПРОИЗВ(В2:С2; В10:С10)

В ячейке F10 размещается значение правой части первого ограничения.

В ячейки В11, С11 размещаются коэффициенты балансового уравнения. В ячейке D11 вычисляется левая часть балансового уравнения по формуле:

=СУММПРОИЗВ(В2:С2; В11:С11)

В ячейке F11 размещается значение правой части первого ограничения.

Затем вызывается процедура «Поиск решения» и открывается диалоговое окно, в котором размещается ссылка на целевую ячейку (риск портфеля), характер экстремума (минимальное значение), указываются адреса изменяемых ячеек ( искомые доли активов х₁ и х₂). В поле «Ограничения» через кнопку «Добавить» устанавливается тип отношений между левыми и правыми частями ограничений и вводится условие неотрицательности переменных (х₁, х₂ >= 0). Нажимается кнопка выполнить, процессор извещает о том, что решение найдено и заполняет таблицу.

Анализ данных таблицы показывает, что оптимальные доли активов в портфеле составляют: х₁ = 0,4, х₂ = 0,6 . При этом минимальный риск портфеля равен 6.19% и доходность портфеля равна 10,8% . Поскольку параметры активов взяты из Примера 7.1, то решение задачи можно найти в таблице этого примера (портфель 9).

Рассмотренный способ решения позволяет решать задачи большей размерности, но в этом случае риск портфеля необходимо вычислять через корреляционную или ковариационную матрицу.

Модель Марковица может использоваться как инструмент построения линии эффективной границы портфеля, состоящего из трех и более активов. Задавая с интервалом значения правой части ограничения по доходности, постепенно уменьшая её от максимальной, получим соответствующие им значения портфельных рисков. Знание эффективной границы портфеля позволяет включать в него безрисковый актив, что расширяет возможности инвестора в части управления доходностью и рисом портфеля.

Задачи по вариантам.

В состав портфеля включены два актива: актив А объемом Х₁ и актив Б объемом Х₂. Объемы активов измеряются в долях. Х₁ + Х₂ =1, Х₁ ,Х₂ ≥ 0. Каждый актив характеризуется средними ожидаемыми значениями доходности m_i и риска σ_i . Взаимосвязь доходностей активов характеризуется коэффициентом парной корреляции r_ij . Параметры активов приведены в нижеследующей таблице .

Требуется:

1. Построить линию эффективной границы портфеля для разных сочетаний Х₁ ,Х₂ в координатах доходность - риск;

2. Сформулировать и решить средствами Excel задачу определения оптимальной структуры портфеля, обеспечивающей минимальный риск портфеля и доходность не ниже 0.8m_Б ( задача Марковица ).

3. Литература:

1. Брусов П.Н. Финансовая математика: Учебное пособие / П.Н. Брусов, П.П. Брусов, Н.П. Орехова, С.В. Скородулина. – 2-е изд., стер. – М.: КНОРУС, 2013. -224с. – (Бакалавриат)

2. Брусов П.Н. Финансовая математика: Учебное пособие / П.Н. Брусов, П.П. Брусов, Н.П. Орехова, С.В. Скородулина. – М.: КНОРУС, 2010. -224с. – (Бакалавриат)

3. Брусов П.Н. Задачи по финансовой математике: Учебное пособие / П.Н. Брусов, П.П. Брусов, Н.П. Орехова, С.В. Скородулина. – М.: КНОРУС, 2012. -272с. – (Бакалавриат)

4. Малыхин В.И. Финансовая математика: Учеб. пособие для Вузов. – 2-е изд., перераб. и доп. – М.: ЮНИТИ - ДАНА, 2012. -237с.

5. Алиев В.С. Практикум по бизнес – планированию с использованием программы Projtct Expert: учебное пособие / В.С. Алиев. – 2-е изд., перераб. И доп. – М. : ФОРУМ : ИНФРА-М, 2010. – 288 с. :ил. – (Высшее образование).

6. Ширшов Е.В. Финансовая математика: Учебное пособие / Е.В. Ширшов, Н.И. Петрик, А.Г. Тутыгин, Т.В. Меньшикова . – 5-е изд., перераб. и доп. – М.: КНОРУС, 2010. -144с.

7. Барбарумов В.Е. Сборник задач по финансовым инвестициям / В.Е. Барбарумов, И.М. Гладких, А.С. Чуйко. – М.: Финансы и статистика, 2004. – 352с.

8. Уродовских В.Н. Управление рисками предприятия: Учеб. пособие. - М.: Вузовский учебник: ИНФРА – М, 2011. – 168с.

9. Финансовая математика: Математическое моделирование финансовых операций: Учеб. пособие/Под ред. В.А. Половникова и А.И. Пилипенко. – М.: Вузовский учебник, _ 2004, 360с.

10. Оценка и анализ рисков: Учебно-методическое пособие. Для студентов VI курса по специальности 060400 «Финансы и кредит» специализация «Финансовый менеджмент» / ВЗФЭИ – М.:Финстатинформ, 2002. – 64с.

11. Оценка и анализ рисков. Компьютерный лабораторный практикум для студентов шестого курса, обучающихся по специальности 080105.65 «Финансы и кредит», специализация - «Финансовый менеджмент». — М.: ВЗФЭИ, 2011.

12. Оценка и анализ рисков. Методические указания по выполнению лабораторной работы на ПЭВМ для самостоятельной работы студентов VI курса (первое высшее образование) и V курса (второе высшее образование) специальности 060400 «Финансы и кредит» специализации«Финансовый менеджмент». — М.: ВЗФЭИ, 2008.

13. Финансовая математика. Методические указания по выполнению лабораторной работы на ПЭВМ для самостоятельной работы студентов IV курса (первое высшее образование) специальности 060400 «Финансы и кредит». — М.: ВЗФЭИ, 2008.

Не нашли, что искали? Воспользуйтесь поиском по сайту: