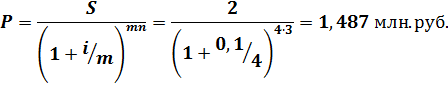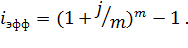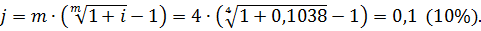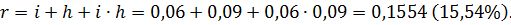|
|
Примеры решения задач по теме 1.ФГБОУ ВПО «Вятский государственный университет» Факультет экономики и менеджмента Кафедра «Методы и модели в экономике» ОСНОВЫ ФИНАНСОВЫХ ВЫЧИСЛЕНИЙ Методические указания по выполнению контрольной работы для студентов направлений подготовки 080100.62 «Экономика», 080200.62 «Менеджмент»
Киров 2014 ББК 65.23 Методические указания разработали доктор физико-математических наук, заведующий кафедрой «Методы и модели в экономике» А.В.Шатров кандидат технических наук, доцент кафедры «Методы и модели в экономике» А.Д. Голубев
Основы финансовых вычислений: методические указания по выполнению контрольной работы студентами направлений подготовки 080100.62 «Экономика», 080200.62 «Менеджмент» А.В. Шатров, А.Д. Голубев. – Киров: Вятский государственный университет, 2014.- 71.
Ó ФГБОУ ВПО Вятский государственный университет, 2014
Содержание
Введение Цели контрольной работы – усвоение теоретических основ курса, выработка навыков в решении задач, соответствующих рабочей программе дисциплины, овладение методами финансовых вычислений с использованием стандартных и прикладных компьютерных программ. 1. Методические указания по выполнению и оформлению контрольной работы Методические указания по выполнению контрольной работы Контрольная работа по дисциплине «Основы финансовых вычислений» содержит конкретные задачи по различным темам курса. Для каждой задачи следует сформировать её математическую модель, привести подробное решение и сделать обоснованные экономические выводы. Численное решение задач, в тех случаях, где это целесообразно, следует подкрепить использованием компьютерных технологий. Порядок оформления контрольной работы Контрольная работа выполняется и защищается в установленные преподавателем сроки. Титульный лист контрольной работы должен содержать все необходимые реквизиты: названия университета и факультета; направление подготовки; наименование учебной дисциплины; номер зачетной книжки, Ф.И.О. студента и преподавателя, дату сдачи работы на проверку. Работа без указания номера зачетной книжки проверке не подлежит, при отсутствии Ф.И.О. преподавателя установленные сроки проверки работы могут быть нарушены. Решение заданий контрольной работы следует сопровождать необходимыми комментариями, т.е. все основные этапы решения задачи должны быть раскрыты и обоснованы на основе соответствующих теоретических положений. При решении задач целесообразно использование компьютерных программ. К собеседованию допускаются студенты, выполнившие правильно и в достаточном объеме все задания контрольной работы. Для получения зачета по результатам собеседования студент должен выполнить работу над ошибками в проверенной преподавателем контрольной работе, знать теоретические основы методов решения всех заданий и уметь ответить на конкретные вопросы, связанные с последовательностью решения. Контрольная работа состоит из семи задач по соответствующим темам. Номер задачи по темам выбирается по первой букве фамилии в соответствии с таблицей
Задания контрольной работы Тема 1. Простые проценты Методические указания. Обозначения: S – наращенная (будущая ) сумма; P– первоначальная сумма; i– ставка простых процентов за период ( в долях ); n – число периодов начисления по ставке i за период. Если nисчисляется в годах, то i– ставка простых процентов годовых ( в долях ). Если срок начисленияt не кратен шагу, то n = t/K , где К – длина шага в днях. Наращенная (будущая ) сумма платежа Р вычисляется по формуле: где I= Pni – сумма процентных денег. Приведение будущей суммы к более раннему моменту времени называется дисконтированием.Формула математического дисконтирования имеет вид:
Второй сомножитель в правой части называется дисконтным множителем (коэффициентом дисконтирования). Величина D = S – P называется дисконтом. При банковском расчете процентов применяется учетная ставка:
Размер дисконта или учета, удерживаемого банком, равен D = S∙n∙d , откуда
Примеры решения задач по теме 1. Пример 1.1.Кредит вобъеме 90 тыс. руб. выдан на срок 2,5 года при ставке простых процентов, равной 12% годовых. Определить единовременную сумму погашения кредита и величину накопленных процентов. Решение: Накопленная сумма процентов: I = P∙n∙i = 90∙2,5∙0,12 = 27 тыс. руб. Наращенная сумма кредита: S = P + I = 90 + 27 = 117 тыс. руб. Пример 1.2.Кредит вобъеме 90 тыс. руб. выдан на срок с 25 февраля 2013 до 9 апреля 2013 года при ставке простых процентов, равной 12% годовых. 1) Рассчитать точные проценты с точным числом дней займа; 2) Рассчитать обыкновенные проценты с точным числом дней займа; 3) Рассчитать обыкновенные проценты с приближенным числом дней займа. Решение: Для расчетов используют формулу I = P•(t/K)• i , 1) I = P∙n∙i = 90∙(44/365)∙0,12 = 1301,92 руб. 2) I = P∙n∙i = 90∙(44/360)∙0,12 = 1320,00 руб. 3) I = P∙n∙i = 90∙(43/360)∙0,12 = 1290,00 руб. ( продолжительность марта – 30 дней). Вычисление отношения t/K можно автоматизировать с помощью функции Excel ДОЛЯГОДА(нач_дата;кон_дата;базис), находящейся в категории функций «Дата и время». Значения параметра «базис» приведены в таблице 1. Таблица1. Значение базиса для функции ДОЛЯГОДА
Пример 1.3.Известно, что через 150 дней должник по договору уплатит 200 000 руб. Кредит выдан под 15% годовых (проценты обыкновенные). Рассчитать первоначальную сумму кредита и дисконт. Решение: P = S/ (1+ni) = 200000/ (1+ 150/360•0.15) = 188 235 руб. , D = S – P = 200000 – 188235.3 = 11765 руб. Пример 1.4.Известно, что через 150 дней предприятие должно получить по векселю 200 000 руб. Банк приобрел вексель с дисконтом и учел его по учетной ставке 15% годовых (год равен 360 дням). Рассчитать полученную предприятием сумму P и дисконт D. Решение: D = S∙n∙d = 200000∙(150/360)∙ 0,15 = 12500 руб. P = S – D = 200000 – 12500 = 187500 руб. Пример 1.5.По договору предприятие должно уплатить через 15 0 дней 4 млн. руб. с процентами, начисляемыми по ставке простых процентов i=15 % годовых. Погашение задолженности было учтено банком за 60 дней до срока погашения по учетной ставке d =11%. Требуется найти сумму, полученную при учете. (В этом примере одновременно используется наращение по ставке i и дисконтирование по учетной ставке d) Решение: P = S(1+n1∙i)∙ (1- n2∙d) = 4∙( 1 + 150/365∙0,15)∙( 1 – 60/ 360∙ 0,11= 4,168721 млн. руб. Пример 1.6. Три платежа S1 = 2 млн. руб., S2 = 3 млн. руб., S3 = 4 млн руб. со сроками уплаты соответственно через 80 , 100 и 150 дней заменяются одним со сроком уплаты через 120 дней при простой ставке 15%. Найти сумму консолидированного платежа (год принять равным 360 дней). Правила консолидации платежей: 1. если все сроки выплат меньше срока консолидации, то суммы выплат наращиваются к сроку консолидации; 2. если все сроки выплат больше срока консолидации, то суммы выплат дисконтируются к сроку консолидации; 3. если часть платежей должна осуществляется ранее срока консолидации, а часть – позднее, то платежи со сроком выплат расположенные левее срока консолидации – наращиваются к сроку консолидации, а лежащие правее - дисконтируются. Обобщенная формула имеет вид:
где n0 – дата консолидации; nj – сроки более ранних выплат (nj < n0); nк – сроки более поздних выплат (nк > n0). Решение: За базовую дату примем день выплаты консолидированного платежа S0 = 120 дней . Т.к. срок объединяемых платежей S1 и S2 меньше срока приведения, то их приведение к моменту выплаты консолидированного платежа будет выполняться с помощью операции наращения, а платеж S3 со сроком большим срока консолидации, будет дисконтироваться:
Задача 1.7. Фирма, в погашение задолженности банку за предоставленный кредит под 30% годовых, должна произвести 2 платежа в сроки 13.06.2013 (164-й день), 1.10.2013 (274-й день) суммами S1 = 1,5 млн. руб. и S2 = 4,5 млн. руб. Фирма договорилась объединить оба платежа в один суммой S0 = 7 млн. руб. с продлением срока выплаты. Найти срок выплаты консолидированного платежа. (В скобках указан порядковый номер даты платежа). Решение: Задача решается в два шага. Сначала определяется современная стоимость консолидируемых платежей:
Затем рассчитывается срок выплаты консолидированного платежа по формуле:
Задача 1.8.Начальный капитал 10 млн. руб. Найти наращенную сумму через 8 месяцев по: 1) ежегодной ставке 15 %; 2) ежемесячной ставке 2 %; 3)квартальной ставке 6 %. Решение: В любом варианте время начисления согласуется с шагом начисления процентов: 1) S = 10∙( 1 + 8/12∙0,15 ) = 11 млн. руб.; 2) S = 10∙( 1 + 8∙0,02 ) = 11,6 млн. руб.; 3) S = 10∙( 1 + 8/3∙0,06 ) = 11,6 млн. руб. Задача 1.9.Векселедержатель предъявил для учета вексель на 8 млн.руб. со сроком погашения 30.09.13. Вексель предъявлен 10.09.13. Какую сумму получит векселедержатель, если: 1) вексель погашается по учетной ставке d = 0,4; 2) вексель погашается по процентной ставке i = 0,4. Решение: 1) P = S( 1 – n∙d) = 8(1 – 20/360∙0,4 ) = 7,822 млн. руб.; 2) P = S / ( 1 + n∙i) = 8 / (1 + 20/360∙0,4 ) = 7,826 млн. руб.; Вексель выгоднее учитывать по процентной ставке, в этом случае векселедержатель получает большую сумму. Задача 1.10.Предприятие получило кредит на 1 год в размере 50 млн. с условием возврата 70 млн. Найти доходность операции для кредитора в виде процентной и дисконтной (учетной) ставок. P = 50 млн., S = 70 млн. В формулах наращения по процентной и учетной ставке со сроком n, то получим, формулы доходности или эффективности по простой ставке процентов и учетной ставке соответственно:
Решение:
Дисконтная (учетная) ставка всегда дает меньшую доходность , чем процентная, ибо она учитывает изменение стоимости денег во времени. Задача 1.11. Кредитор и заемщик договорились, что из суммы кредита, выданного на 250 дней, сразу удерживается дисконт в размере 20% указанной суммы. Требуется определить цену кредита в виде простой годовой учетной ставки d и годовой простой ставки i. Год полагать равным 365 дней. В данном контракте дисконт фиксируется от конечной суммы независимо от срока займа. Таким образом, уровень процентной ставки задается в неявном виде. Пусть S- размер погасительного платежа (сумма ссуды к концу срока), dn – доля этого платежа, определяющая величину дисконта за весь срок ссуды. Р = S(1 – dn) – реально выдаваемая ссуда в момент заключения договора. Решение:
Задачи по вариантам Задача 1.Банк дает кредитыпод ставку 10% годовых. Рассчитать месячную ставку простых процентов. Задача 2.Ссуда размером 250 тысяч руб. выдана на 5 лет по 12% простых процентов годовых. Определить наращенную сумму. Задача 3.Ссуда размером 250 тысяч руб. выдана на 5 лет по 12% простых процентов годовых. Определить , во сколько раз изменится наращенная сумма, если ставку уменьшить на 1,5%. Задача 4.По какой ставке простых процентов годовых необходимо отдать в рост капитал, чтоб первоначальный капитал в размере 180 тыс. руб. за 182 дня увеличился в 1,1 раза. Задача 5.Цена актива равняется 1000 рублям. Его годовая доходность составила 15%. Определить, по какой цене был куплен актив. Задача 6.Через 60 дней после подписания договора должник уплатит 2 000 000 руб. Кредит выдан на условиях 12% годовых (проценты простые). Какова первоначальная сумма займа. Рассчитать дисконт. Задача 7.Через 60 дней предприятие должно получить по векселю 2 000 000 руб. Банк приобрел вексель с дисконтом. Банк учел вексель по учетной ставке 12% годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт. Задача 8.Три платежа S1 =5 млн. руб., S2 =1 млн. руб., S3 =4 млн. руб. со сроками уплаты соответственно через 80, 140 и 120 дней заменяются одним платежом со сроком уплаты через 180 дней по простой ставке 20%. Найти сумму консолидированного платежа (год принять равным 360 дней). Задача 9.Фирма, в погашение задолженности банку за предоставленный кредит под 30% годовых, должна произвести 2 платежа в сроки 2.05 (122-й день),20.08 (232-й день) суммами S1 = 3 млн. руб. и S2 = 2 млн. руб. Фирма договорилась объединить оба платежа в один суммой S0= 5 млн. руб. с продлением срока выплаты. Найти срок выплаты консолидированного платежа. Задача 10. Две суммы10 и 12 млн. руб. должны быть выплачены 29.08.13 (241) и 1.01.14 (1). Стороны договорились пересмотреть условия контракта: должник 1.12.13 (335) выплачивает 10 млн. руб., остаток долга гасится 1.04.14 (91). Найти эту сумму при условии, что пересчет осуществляется по ставке простых процентов, равной 12% (год равен 365 дней). Задача 11. Покупатель приобрел телевизор по цене 20 000 руб., в кредит, уплатив сразу 5 000 руб. и обязавшись уплатить остальное в течение 12 месяцев, делая ежемесячные равные платежи. Какую сумму он должен выплачивать, если продавец требует за кредит 4% простых в год? Задача 12. Финансовая компания дает ссуду 500 000 руб. на 3 года под простой процент, равный 6% в год. Какую сумму получит клиент в момент получения ссуды? Методические указания: при расчетах использовать схему простого дисконта. Задача 13. Фирма берет в банке ссуду размером 50 000 руб. на 3 месяца под 8% простого дисконта . Какую сумму она должна вернуть через три месяца? Методические указания: при расчетах использовать схему простого дисконта. Задача 14. Фирма обещалась заплатить за полученное от города помещение 1 200 т.руб. через 5 лет и еще 500 т.руб. через 8 лет относительно момента заключения договора. В силу сложившихся обстоятельств, фирма решила пересмотреть условия сделки: 700 т.руб. выплатить через 3 года, а остальной долг погасить через 6 лет. Какая сумма должна быть выплачена через 6 лет при условии начисления 8% простых годовых. Задача 15. Транспортная компания собирается приобрести станок стоимостью 550 000 руб. У компании есть два варианта схемы финансирования: либо выплатить цену станка в течение 5 лет по 110 000 руб. в конце каждого года, либо в момент покупки заплатить 150 000 руб., а затем выплачивать в течение четырех лет по 100 000 руб. Выяснить, какой вариант выгоднее, при условии, что стоимость капитала составляет 14% простых годовых. Задача 16.Банк дает кредитыпод ставку 15% годовых. Рассчитать месячную ставку простых процентов. Задача 17.Ссуда размером 150 тысяч руб. выдана на 6 лет по 10% простых процентов годовых. Определить наращенную сумму. Задача 18.Ссуда размером 200 тыс. руб. выдана на 7 лет по 15% простых процентов годовых. Определить во сколько раз изменится наращенная сумма, если ставку уменьшить на 1,5%. Задача 19.По какой ставке простых процентов годовых необходимо отдать в рост капитал, чтоб первоначальный капитал в размере 300 тыс. руб. за 224 дня увеличился в 1,2 раза. Задача20.Цена актива равняется 15 000 рублям. Его годовая доходность составила 12%. Определить, по какой цене был куплен актив. Задача 21.Через 60 дней после подписания договора должник уплатит 1500 000 руб. Кредит выдан на условиях 11% годовых (проценты простые). Какова первоначальная сумма займа. Рассчитать дисконт. Задача 22.Через 120 дней предприятие должно получить по векселю 1 000 000 руб. Банк приобрел вексель с дисконтом. Банк учел вексель по учетной ставке 14% годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт. Задача 23.Три платежа S1 =4 млн. руб., S2 =2 млн. руб., S3 =3 млн. руб. со сроками уплаты соответственно через 70, 120 и 140 дней заменяются одним платежом со сроком уплаты через 200 дней по простой ставке18%. Найти сумму консолидированного платежа (год принять равным 360 дней). Задача 24. Фирма, в погашение задолженности банку за предоставленный кредит под 25% годовых, должна произвести 2 платежа в сроки 2.05 (122-й день), 18.08 (230-й день) суммами S1 = 4 млн. руб. и S2 = 1 млн. руб. Фирма договорилась объединить оба платежа в один суммой S0= 5 млн. руб. с продлением срока выплаты. Найти срок выплаты консолидированного платежа. Задача 25. Две суммы ,12 и 10 млн. руб., должны быть выплачены 23.08.13 (235) и 11.01.14 (11). Стороны договорились пересмотреть условия контракта: должник 6.12.13 (340) выплачивает 12 млн. руб., остаток долга гасится 1.04.14 (91). Найти эту сумму при условии, что пересчет осуществляется по ставке простых процентов, равной 12% (год равен 365 дней). Задача 26. Покупатель приобрел телевизор по цене 3 000 руб., в кредит, уплатив сразу 600 руб. и обязавшись уплатить остальное в течение 12 месяцев, делая ежемесячные равные платежи. Какую сумму он должен выплачивать, если продавец требует за кредит 6% простых в год? Задача 27. Финансовая компания дает ссуду в 800 000 руб. на 4 года под простой процент, равный 8% в год. Какую сумму получит клиент в момент получения ссуды? Методические указания: при расчетах использовать схему простого дисконта. Задача 28. Фирма берет в банке ссуду размером 800 000 руб. на 4 месяца под 10% простого дисконта. Какую сумму она должна вернуть через три месяца? Методические указания: при расчетах использовать схему простого дисконта. Задача 29. Фирма обещалась заплатить за полученное от города помещение 1 500 т.руб. сегодня и еще 500 т.руб. через 8 лет относительно момента заключения договора. В силу сложившихся обстоятельств, фирма решила пересмотреть условия сделки: 300 т.руб. выплатить через 3 года, а остальной долг погасить через 6 лет. Какая сумма должна быть выплачена через 6 лет при условии начисления 8% простых годовых. Задача 30. Транспортная компания собирается приобрести станок стоимостью 800 000 руб. У компании есть два варианта схемы финансирования: либо выплатить цену станка в течение 5 лет по 160 000 руб. в конце каждого года, либо в момент покупки заплатить 200 000 руб., а затем выплачивать в течение четырех лет по 150 000 руб. Выяснить, какой вариант выгоднее, при условии, что стоимость капитала составляет 12% простых годовых.
Тема 2. Сложные проценты Методические указания. Формула наращения по сложным процентам:
Если начисления процентов по периодам различны, то вычисление S осуществляется по формуле:
Формула наращения по сложным процентам при начислении процентов m раз за год:
Эффективная ставка показывает, какая годовая ставка сложных процентов даст такой же результат, как m – разовое начисление процентов в год по ставке i/m:
Если эффективная ставка начисления сложных процентов (за месяц, квартал, полугодие) известна, то можно рассчитать номинальную годовую ставку по формуле:
Математическое дисконтирование (учет) про сложной ставке процентов:
где νn – дисконтный или учетный множитель. Если проценты начисляются m раз в году, то приведенная к началу операции сумма определится выражением:
Дисконтирование по банковской ставке сложных процентов осуществляется по формуле
где dсл – сложная годовая учетная ставка. Дисконт в этом случае равен
Формулы для определения процентной ставки i и продолжительности операции n (mn) получаются из предыдущих формул:
если проценты начисляются раз в году;
если проценты начисляются m раз в году. Формулы показывают, что величина любого из параметров S, P, n, i может быть определена по известным трем остальным. Примеры решения задач: Пример 2.1. Сумма, равная 600 тыс. руб., дается в займы на 3 года под 15% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты. Решение: 1) Сложные проценты:
Доход равен 912 – 600 = 312 тыс. руб. 2) Простые проценты:
Доход равен 870 – 600 = 270 тыс. руб. Пример 2.2. Сумма, равная 600 тыс. руб., инвестируется на 4 месяца под 15% годовых. Сравнить наращенные суммы и суммы процентов за этот срок, используя простую и сложную процентные ставки. Решение: 1.Сложные проценты:
Сумма процентов 628,6 – 600 = 28,6 тыс. руб. 2. Простые проценты:
Сумма процентов 630– 600 = 30 тыс. руб. Итак, если срок наращения меньше интервала наращения, то выгоднее наращивать капитал по простым процентам.
Пример 2.3. Найти сумму долга в 20 млн. руб. через 8 месяцев, 200 дней, 4 года, 8 лет по сложным годовым ставкам 10% и 15%. Решение: Расчетная формула:
1) i = 10%:
2) i = 15%:
Сумма долга растет с увеличением и процентной ставки, и числа лет начисления. Пример 2.4.В банк на депозит положена сумма в 5 млн. руб. на 2 года по ставке процента 20% годовых сложных. Определить наращенные суммы при ежемесячном, ежеквартальном, полугодовым и годовым начислением процентов. Решение: Расчет производится по формуле:
где m – количество начислений процентов в году ( 12, 4, 2, и 1).
Итак, чем чаще капитализируются процентные начисления, тем больше сумма наращения. Пример 2.5.На сумму 5 млн. руб. начислить проценты по непрерывной ставке d =10% годовых 5 лет. Если число начислений процентов в году m ® ¥, то формула наращения принимает вид:
где d- непрерывная ставка годового процента. Решение:
Пример 2.6. Предприятию через 3 года будет выплачена сумма 2 млн. руб. Определить ее современную стоимость при условии, что годовая ставка сложных процентов составляет 10% годовых, а начисление процентов осуществляется ежеквартально.
Пример 2.7. Рассчитать эффективные ставки процентов за 1 год при ежегодном, полугодовом, квартальном, ежемесячном и ежедневном начислении процентов, если номинальная годовая ставка j = 20%. Решение: Формула для расчета эффективной ставки имеет вид:
С учетом этой формулы, имеем: 1) m = 1 (ежегодное начисление) iэфф = (1+ 0,2 / 1)1 – 1 = 0,2 ( 20% ); 2) m = 2 (полугодовое начисление) iэфф = (1+ 0,2 / 2)2 – 1 = 0,21 ( 21% ); 3) m = 4 (полугодовое начисление) iэфф = (1+ 0,2 / 4)4 – 1 = 0,2155 ( 21,55% ); 4) m = 12 (ежемесячное начисление) iэфф = (1+ 0,2 / 12)12 – 1 = 0,2194 ( 21,94% ); 5) m = 365 (ежедневное начисление) iэфф = (1+ 0,2 / 365)365 – 1 = 0,2213 ( 22,13% ). Пример 2.8.Найти номинальную годовую процентную ставку, если эффективная годовая ставка при ежеквартальном начислении процентов равна 10,38%. Решение: Номинальная ставка рассчитывается по следующей формуле:
Пример 2.9.Найти номинальную годовую процентную ставку, если квартальная эффективная ставка равна 3 %. Решение: Уравнение эквивалентности ставок имеет вид:
Пример 2.10.Какую ставку должен назначить банк, чтобы при годовой инфляции в 9%, реальная ставка оказалась 6%? Банк при годовом темпе инфляции в 9% рассчитывает получить реальную ставку 7%. Как должна быть скорректирована ставка процента? Решение: Скорректированная банковская ставка r (брутто-ставка) находится из выражения:
где i – реальная ставка; h – темп инфляции. Из формулы находим:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

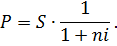
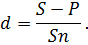

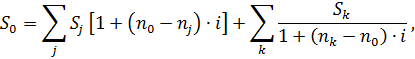
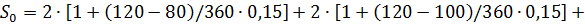

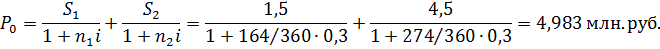

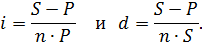
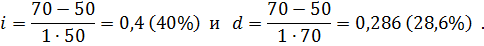
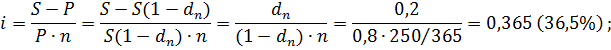
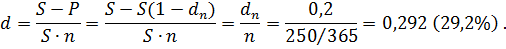

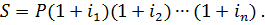

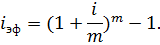
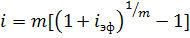 .
.
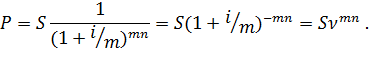

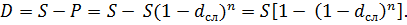

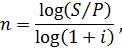

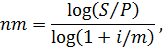

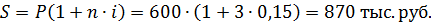

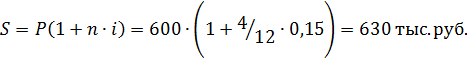



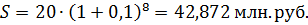
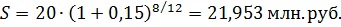
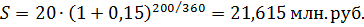

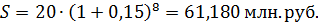


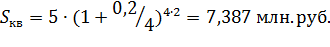
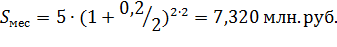
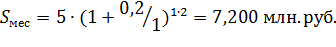
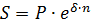 ,
,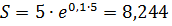 млн. руб.
млн. руб.