|
|
Ведомость координат разомкнутого теодолитного хода
Примечание. Автор обращает Ваше внимание на то, что в этой таблице (кружеве) и заключена, в частности, красота и логика обработки теодолитного хода.
Поправки в углы Далее вычисляют дирекционные углы сторон теодолитного хода последовательно по ходу по формулам (7.62) с учетом исправленных горизонтальных углов:
Вычисления продолжаются до получения дирекционного угла конечной стороны хода
79.3. Вычисление приращений координат и оценка точности хода Приращения координат (прямая геодезическая задача) вычисляют по формулам (7.3):
Запишем схему передачи координат с начальной точки хода на конечную в виде системы уравнений и составим суммы этих уравнений:
Поскольку значения ХН , ХК, YH , YK являются исходными (известными), то по результатам вычислений можно получить невязки в приращениях координат:
Рис. 7.23. Физический смысл невязок в приращениях координат.
Физический смысл невязок в приращениях координат пояснен на рис. 7.23. При построении теодолитного хода реальное его положение определяется точками А, 1, 2, …, В, жёстко закреплёнными на местности и имеющими абсолютно точные, но неизвестные нам координаты. В результате неизбежных погрешностей в измерениях (углов и расстояний) и возможных погрешностей при вычислениях получается реальный ход А-1'-2'- … - В', т.е. ход, не замыкающийся в конечной исходной точке В. Величина незамыкания хода (невязка) по оси Х – fX , по оси Y – fY. Эти невязки могут быть получены и как разности координат:
Общая линейная (абсолютная) невязка хода составляет
Очевидно, что сама абсолютная (линейная) невязка не всегда может являться непосредственным критерием качества измерений, поскольку длины ходов могут быть различными при одном и том же значении абсолютной невязки. В связи с этим для оценки точности теодолитных ходов пользуются относительной невязкой, определяемой по формуле
где Критерием качества работ является выполнение условия
Величина допустимой относительной невязки
Пример 7.14.Оценка качества теодолитного хода. Исходные данные см. в табл. 7.7 (ведомость координат). В ведомости координат выполнены вычисления приращений координат и получены их суммы по всему ходу:
79.4. Рекомендации к поиску вероятных погрешностей в измерениях и вычислениях при обработке ведомости координат Конечная оценка точности теодолитного хода производится на основе всех (линейных и угловых) измерений, выполненных при создании съёмочного обоснования. Кроме того, оценке точности теодолитного хода предшествует и большой объём вычислений, что, даже несмотря на ряд контрольных вычислений, повышает вероятность появления погрешностей, в результате чего условие (7.60) может не выполниться. Чаще всего отступление от неравенства (7.60) сравнительно небольшое, что как раз и затрудняет поиск погрешностей. Грубые погрешности (просчеты) находятся сравнительно быстро и легко. В некоторых случаях, если небольшие погрешности допущены при измерениях в двух или нескольких линиях (в углах или расстояниях), то отыскание их только в камеральных условиях чаще всего не представляется возможным. Необходимы повторные измерения, которые обычно начинают с самых сложных участков. Если же погрешности были допущены только в одной линии (в её длине или её направлении), то поиск их может быть сравнительно легко осуществлен по величинам и знакам невязок fХ и fY в приращениях координат. Для этого предварительно определяют дирекционный угол линейной невязки fАБС, по той же схеме, как это производится при решении обратной геодезической задачи при определении дирекционных углов исходных направлений Затем следует образовать группы дирекционных углов: А → совпадающих с направлением невязки (af ± 180o); Б → перпендикулярных к направлению невязки [( af + 90o) ± 180o]. Если погрешность допущена в длине линии, то наиболее вероятно, что она присутствует в тех линиях, для которых их направление (дирекционный угол) совпадает с направлением невязки (сравнение производится по группе А). Так, например, наиболее вероятна погрешность в длине линии С-5 для разомкнутого теодолитного хода (рис. 7.23 а) либо для линий 4-1 и 2-3 для замкнутого теодолитного хода (рис. 7.23 б). Если погрешность допущена в направлении линии, то наибольшая вероятность этого для тех линий, дирекционные углы которых отличаются от направления невязки на 90о. (Сравнение производится по группе В). Таким образом, для разомкнутого теодолитного хода, изображенного на рис. 7.23 а, наиболее вероятна погрешность в направлении линии 6-В. Для замкнутого теодолитного хода, как это следует из рисунка, более вероятна погрешность в направлении линий 1-2 и 3-4 . В том случае, если указанный алгоритм поиска погрешностей не даст результатов, то следует ожидать, что погрешности присутствуют в двух или более линиях. Это требует повторения полевых измерений, перед которыми необходимо ещё раз внимательно выверить полевые журналы предшествующих работ, а также повторно проверить все вычисления. Повторные полевые измерения целесообразно начинать с проверки длин линий и их горизонтальных проложений (при этом в первую очередь проверяют наиболее сложные для измерений участки). Проверку горизонтальных углов также начинают с вершин, наблюдения с которых по каким-либо причинам выполнялись с большими помехами: видимость соседних пунктов была недостаточной, производилась перестановка вех и т.п. Особое внимание здесь следует уделять центрированию теодолита и устнановке вехи в наблюдаемых точках.
Пример 7.15.Поиск вероятных погрешностей в теодолитных ходах. Исходные данные см. в табл. 7.7 (ведомость координат). Рассмотрим результаты обработки данных, приведённые в табл. 7.7. (На самом деле невязки в ходах допустимы, в связи с чем нет необходимости в поиске погрешностей). Данный пример приводится исключительно в учебных целях только для пояснения схемы поиска погрешностей измерений в теодолитных ходах.
В соответствии со значениями дирекционных углов линий теодолитного хода наиболее близким является a4D » 118о и a34 » 57о. Таким образом, можно предположить, что существует погрешность в определении направления линии 4-D (эта погрешность может быть и грубой. Неправильно, например, выписано значение дирекционного угла в ведомость координат, а также возможна погрешность в измерении длины линии 3-4). При определенном навыке оценки величин дирекционных углов выполняются без вычислений, по значениям невязок и их знакам.
79.5. Уравнивание приращений координат и вычисление координат точек хода В приращения координат, при обеспечении условия (7.80), вводят весовые поправки
Величины поправок в технических теодолитных ходах округляют до 0,01 м. Суммы полученных поправок должны полностью компенсировать невязку:
Контроль! Из-за округлений значений поправок условие (7.83) может не выполниться, в связи с чем в приращения, полученные по большим горизонтальным проложениям следует добавить 0,01 м, а приращения, полученные по меньшим горизонтальным проложениям, уменьшить на такую же величину до достижения условия (7.83). Контроль исправленных приращений координат
заключается в проверке условий
Контроль! Координаты точек теодолитного хода вычисляют последовательно по формулам (7.76) подстановкой в них исправленных значений приращений координат. Вычисление координат конечной точки хода
является контрольным. Полученные вычисленные значения координат конечной точки хода должны точно совпадать (в пределах округлений) с их исходными значениями:
Контроль! Проследите указанный алгоритм обработки теодолитного хода по ведомости координат (табл. 7.7). Обратите внимание на то, что исходные значения координат начальной и конечной точек теодолитного хода в ведомости координат округлены до 0,01 м, как и величины горизонтальных проложений и приращений координат. И ещё обратите внимание на то, что автор восемь раз записал слово Контроль!при обработке ведомости координат. И Вам при вычислениях восемь раз надо остановиться на соответствующем этапе (узелке), чтобы убедиться в выполнении контрольных нормативов. Нельзя перешагнуть через это. Если у Вас появилась ошибка в вычислениях, а Вы не проконтролировали свои действия по соответствующему нормативу, то дальше можно и не вычислять, потому что имеется большая вероятность, что на следующем этапе расчёта ничего хорошего не получится. Контролируйте себя, и Вы избавитесь от лишних ненужных вычислений.
79.6. Обработка ведомости высот
Высоты точек теодолитного хода чаще всего определяют способом геометрического нивелирования (гл. 6). Однако в ряде случаев используют метод тригонометрического нивелирования, в котором превышения точек по принятому направлению хода определяют по формуле (рис. 7.24)
где j – номер точки;
Рис. 7.24. Определение превышений методом тригонометрического нивелирования.
Если на вехе, установленной в точке (j+1), отложить отрезок i (высоту прибора) от её основания, то формула для вычисления превышения упрощается:
Так, для обозначений, приведенных на рисунке, можно записать с учётом условий (7.88) и (7.89):
Составим уравнения последовательной передачи высот с начальной точки теодолитного хода на конечную точку и получим сумму этих уравнений:
По аналогии с вычислениями координат найдем невязку хода в превышениях
Инструкцией для технических теодолитных ходов при создании высотного обоснования для топографической съемки установлено, что допустимая невязка в превышениях должна быть равна
где n – число превышений; 0,04 м коэффициент (0,04 м на 100 м расстояния);
Выполненные работы считаются качественными, если
В противном случае следует проверить полевые журналы, выверить произведенные вычисления либо повторить полевые работы. При выполнении условия (7.93) определяют поправки в превышения по весовой формуле
как и при вычислении поправок в приращения координат. Поправки округляют до 0,01 м, контролируют их сумму (
Таблица 7.8 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
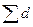681,47 м
722о29,0'
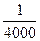
2о28,1'
Во все углы вводим поправки по -0,2' и дополнительно в угол β3 -0,1', образованный короткими сторонами (условие (7.70) обеспечивается. Контроль!). Поправки в углы записывают в ведомость над измеренными углами. Сумма исправленных углов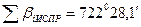 
, что удовлетворяет условию (7.72). Контрол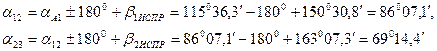ь!
= 
= 
, что показывает, что условие (7.74) выполнено. Контроль!
; 
; 
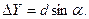
(7.76)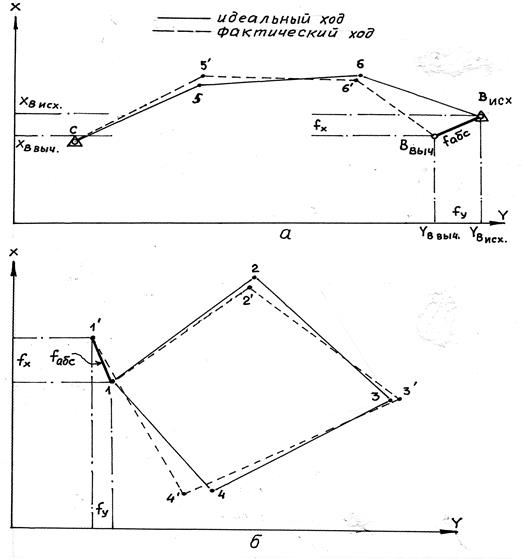
; 
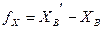(7.77)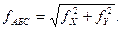
(7.78)
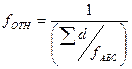, (7.79)
(7.80)
определяется соответствующими инструкциями, а также техническим заданием, устанавливающими необходимую точность построения съёмочного обоснования. Так, для технических теодолитных ходов, в зависимости от условий измерений, особенно длин линий, величина относительной допустимой невязки (погрешности) может находиться в пределах от 1:1000 до 1:3000.
Теоретические разности координат: 
Невязки:
; 
;
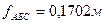(Значение знаменателя относительной невязки можно округлять до пятидесяти). Если заданная допустимая относительная невязка равна, например, 1:2000, то необходимое качество построения съёмочного обоснования обеспечено. Контроль!
(7.81)
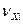и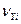 
, зависящие от величины горизонтального проложения, по которому было вычислено данное приращение. Знаки поправок должны быть обратными знаку невязки:
; 
. (7.82)
; 
. (7.83)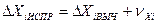
; 
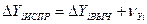(7.84)
; 
. (7.85)
; 
(7.86)
; 
. (7.87)
, (7.88)
- угол наклона; i – высота прибора (расстояние на станции от центра зрительной трубы до верха закрепленной точки); V – высота наведения на точку теодолитного хода, следующую по принятому направлению.
. (7.89)
= 
или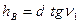 
.
(7.90)
(7.91)
, м , (7.92)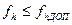
. (7.93)
, (7.94)
) и вводят с учётом знаков превышений и поправок в значения превышений:
. (7.95)