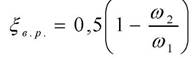|
|
Гидравлически шероховатой (б) труб
Рис. 4.3. Схема опытной установки для определения коэффициен- та гидравлического трения: 1 – трубопровод, 2 – емкость расходная, 3 – пьезометры, 4,5 – вен- тили, 6 – емкость мерная.
23
Величина эквивалентной шероховатости зависит от материа- ла, способа изготовления и соединения труб, от продолжительно- сти эксплуатации. 1. Эквивалентная шероховатость Δ , мм
4.2. Описание опытной установки (рис. 4.3) Испытываемый трубопровод 1, диаметром 26 мм подсоеди- нен к напорному баку 2. В начале и в конце трубопровода уста- новлены пьезометры 3. При проведении опыта вентиль 4 полно- стью открыт, а вентиль 5 служит для изменения расхода воды (следовательно средней скорости υ и числа Рейнольдса Re). Во- домерное стекло мерного банка 6 проградуировано в литрах. Для слива воды из мерного бака служит вентиль 7. Порядок выполнения работы 1. Опыты проводить при открытии вентиля на 1/3, 2/3 и пол- ностью. 2. При помощи секундомера определить время истечения в мерный бак 10 л воды (10·10 -3 м3 ). 3. Замерить разность уровней в пьезометрах, что составляет потери напора hдл. на длине 2,5 м. 4. По полученным значениям расхода из уравнения нераз- рывности Q = ω υ определить скорость воды. 5. Коэффициент кинематической вязкости принять по табли- це
И определить число Рейнольдса по формуле
6. Определить коэффициент λ по опытным данным из фор- мулы (1) и по соответствующим эмпирическим формулам для со- ответствующих значений Запись и обработка опытных данных
4.5. Контрольные вопросы 1. Какие трубы называются гидравлическими гладкими и ше- роховатыми? 2. Что характеризует гидравлический радиус? 3. От каких параметров зависит число Рейнольдса? 4. От каких параметров зависит значение коэффициента при различных числах Рейнольдса? 5. Как выражается формула Дарси-Вейсбаха?
РАБОТА 5.ОПРЕДЕЛЕНИЕ МЕСТНЫХ КОЭФФИЦИЕНТОВ СОПРОТИВЛЕНИЯ Цель работы– углубление знаний студентов в области гид- равлики трубопроводов, опытное определение коэффициента ме- стных сопротивлений и суммарного коэффициента сопротивле- ния системы. Теоретические положения Местные потери напора возникают вследствие внезапного изменения скорости по величине и направлению и зависят в ос- новном от геометрических размеров и форм местных сопротив- лений (внезапное сужение или расширение поперечного сечения труб, резкие повороты и т.д.). Величина местных потерь напора зависит от числа и вида местных сопротивлений. В большинстве случаев при гидравлическом расчете трубопроводов нельзя пре- небрегать местными потерями. Экспериментальные исследования Борда и Беланже показате- ли, что в турбулентном потоке местные потери напора пропор- циональны квадрату скорости в сечении за местным сопротивле- нием: где ξ - коэффициент местного сопротивления; ύ – средняя скорость потока жидкости на расстоянии (5-10) d от местных сопротивлений (здесь d – диаметр трубы). Если диаметр трубопровода и, следовательно, скорость в нем меняется по длине, то за расчетную скорость в нем меняется по длине, то за расчетную скорость принимают большую, т.е. скорость, соответствующую меньшому диаметру трубопровода. Полный напор выражается уравнением Бернулли При горизонтальном трубопроводе z 1 = z 2. Считая режим
движения турбулентными и d1 = d2 = 1,0
Рассмотрим наиболее часто встречающиеся в трубопрово- дах виды местных сопротивлений. 5.1.1. Внезапное расширение потока (рис.5.1). Согласно тео- реме Борда, потери напора при внезапном расширении потока жидкости можно определить по формуле:
где υ1 – средняя скорость движения жидкости в сечении 1-1; υ2 – то же, в сечении 2-2. Из условия неразрывности потока Q = ω1υ1 = ω2υ2 = const
Подставляя эти выражения в формулу 5.4. получим:
Из формул 5.1 и 5.5 имеем:
Числовые значения коэффициента местного сопротивления для внезапного расширения сечения трубы подсчитанные по формуле 5.6.
Рис. 5.1. Внезапное расширение Потока Рис. 5.2. Внезапное сужение потока
5.1.2. Внезапное служение потока (рис. 5.2). При внезапном сужении потока происходит сжатие струи от сечения ω1 до сечения ω2. Коэффициент сопротивления ξв.р. рассчитывается в зависимости от отношения ω1/ω2:
(5.7)
Таблица 5.2
циент местного сопротивления при плавном повороте трубы за- висит от отношения d/R; где d – диаметр трубы; R – радиус закругления. Таблица 5.3
5.1.4. Резкий поворот трубы (рис. 5.4). Коэффициент сопро- тивления при резком переломе трубы зависит от угла перелома α. Таблица 5.5
5.1.5. Задвижка (рис. 5.5). Коэффициент сопротивления за- движки ε,зад зависит от степени ее открывания, т.е. от отношения h/d; где h – высота открывания; d – диаметр отверстия задвижки. Таблица 5.6

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
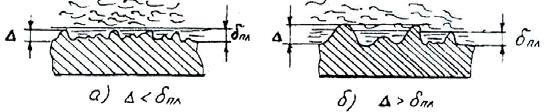
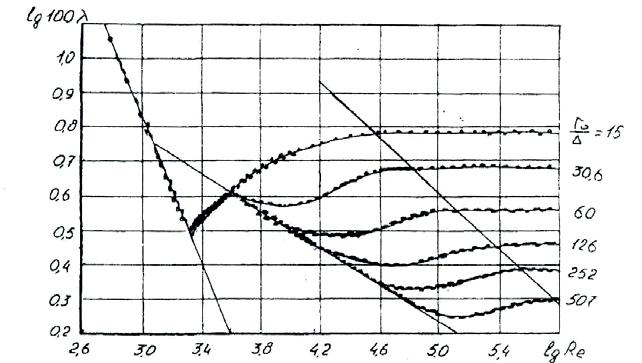
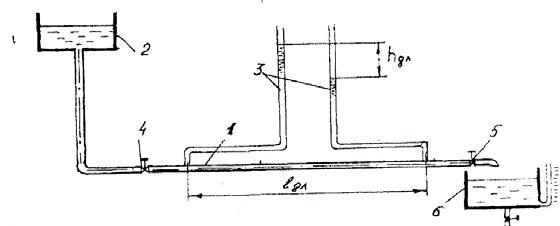

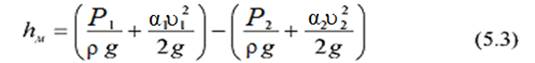



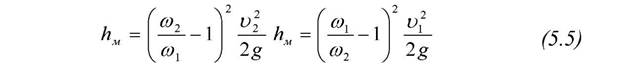

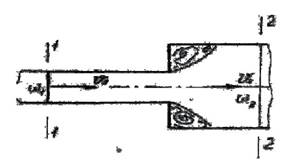
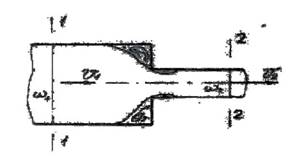


 Рис.5.3. Плавный поворот трубы
Рис.5.3. Плавный поворот трубы
 Рис. 5.4. Резкий поворот трубы
Рис. 5.4. Резкий поворот трубы
 Рис. 5.5. Схема задвижки
Рис. 5.5. Схема задвижки
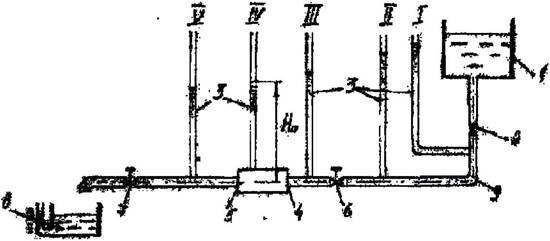 Рис.5.6 Схема установки для определения коэффициента местных сопротивлений:
1-емкость расходная, 2,6 к 7-вентили, 3-пьезометры, 4—внезапное расширение, 5-внезапное сужение, 8-емкость мерная, 9-поворот на 90°
Рис.5.6 Схема установки для определения коэффициента местных сопротивлений:
1-емкость расходная, 2,6 к 7-вентили, 3-пьезометры, 4—внезапное расширение, 5-внезапное сужение, 8-емкость мерная, 9-поворот на 90°