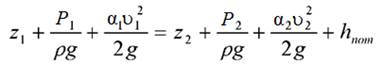Физическое значение числа Рейнольдса можно считать

равными:

Re_кр. = 2000 – 2400 для формулы 2.2 и 2.5

Re_кр. = 500 – 900 для формулы 2.3.

Приведенные значения Re_кр. Относятся к равномерному дви-

жению в трубе или в открытом канале. При ускоренном движе-

12

нии Reкр. возрастает, при замедленном – уменьшается. Шерохова-

тость стенок русла и условия воды также оказывает влияние на

критическое значение числа Рейнольдса.

При Re < Reкр.

Описание опытной установки

Прибор (рис.2.4) состоит из бака 1, к которому присоединена

стеклянная трубка 3. На конце трубки имеется кран 4 для регули-

рования расхода воды. Для раствора красящегося вещества име-

ется бачок 2 с тонкой трубкой, введенной в трубку 3. Для изме-

рения расхода служит мерный бачок 5. Постоянный уровень воды

в баке 1 поддерживается переливным трубопроводом 6.

Порядок проведения работы

1. Наполнить бак 1 водой, а бачок 2 раствором красящегося

вещества. С помощью крана 4 в трубке 3 в начале устанавливает-

ся малый расход, при котором наблюдается ламинарный режим.

При этом струйка краски по всей длине имеет форму тонкой ни-

ти.

2. Для разных значений режимов движения (ламинарный, пе-

реход от ламинарного к турбулентному, турбулентный, переход

от турбулентного к ламинарному) замерить объем воды в мерном

баке, равный 1 · 10 -3 м3 и время t наполнения.

3. Определить кинематический коэффициент вязкости воды

по эмпирическому формуле Пуазейля или по таблице 1 в зависи-

мости от температуры.

Значения кинематического коэффициента вязкости

Воды в зависимости от температуры

Т, с^o
0
5
10
15
20
30

ν, м2 /с 1,78х10 ^-6 1,52х10 ^-6 1,31х10 ^-6 1,14х10 ^-6 1,01х10 ^-6 0,81х10 ^-6

-------------------------------------------------------------------------------------

4. По измеренному объему воды V, площади сечения трубки

ω, времени опыта определить среднюю скорость из уравнения

неразрывности струи: Q = ω · υ

13

5. Для каждого опыта определить число Рейнольдса.

6. Дать заключение

Запись и обработка данных

2.4. Контрольные вопросы

1. В чем состоит основное отличие турбулентного течения от

ламинарного?

2. Как определить число Рейнольдса для трубы прямоугольно-

го сечения?

3. Будет ли изменяться критическое число Рейнольдса при

увеличении шероховатости трубопровода?

4. Как определить гидравлический диаметр?

5. Есть ли отличия между верхним и нижним критическими

числами Рейнольдса?

РАБОТА 3. ОПЫТНАЯ ИЛЛЮСТРАЦИЯ УРАВНЕНИЯ

Д. БЕРНУЛЛИ

Цель работы – показать переход потенциальной энергии в

кинематическую и кинетической энергии в потенциальную при

движении жидкости по трубопроводу переменного сечения. По-

строить пьезометрическую и напорную линии.

Теоретическое положение

Уравнение Д. Бернулли является выражением закона сохра-

нения энергии применительно к потоку жидкости, связывающим

потенциальную (mgH) и кинетическую (mυ2 /2) энергии жидкой

частицы массой m в двух ее положениях. Уравнение Бернулли

является одним из основных уравнений гидравлики, используе-

мых при решении многих практических задач о движении реаль-

ной жидкости.

Уравнение Бернулли для установившегося плавно изменяю-

щегося потока реальной жидкости имеет вид:

Входящие в уравнение слагаемые и уравнение в целом мож-

но интерпретировать с геометрической и энергетической точек

зрения (рис.3.1).

С геометрической точки зрения:

z - высота положения – расстояние от произвольно

выбранной горизонтальной плоскости сравнения О-О

до центра тяжести рассматриваемого сечения потока;

- пьезометрическая высота – высота столба жидкости,

соответствующее гидростатическому давлению в

данной точке живого сечения потока;

- скоростной напор;

пьезометрический напор

гидравлический полный напор.

- коэффициент Кориолиса, или коэффициент ки-

нематической энергии, представляющий собой отношение дей-

ствительной кинематической энергии секундной массы жидко-

сти, протекающий через живое сечение, к кинематической энер-

гии той же массы, условно вычисленной в предположении, что

скорость во всех точках живого сечения равна средней скорости.

При ламинарном режиме α = 2,0, при турбулентном α = 1,05 – 1,1.

hпот. -
потери напора между сечениями 1 и 2.

С энергетической точки зрения:

z - удельная (отнесенная к единице веса) энергия положе-

ни я жидкости в рассматриваемом сечении потока;

- удельная энергия давления;

- удельная кинетическая энергия;

удельная потенциальная энергия

- полная удельная энергия;

- полная удел

Рис. 3.1. Схема к определению пьезометрического и

Скоростного напоров

Рис.3.2. Графическое изображение пьезометрической и

Скоростной линии

Уравнение Бернулли свидетельствуют о том, что по длине

потока жидкости гидравлический напор (полная удельная энер-

гия) уменьшается. Из этого же уравнение вытекает также, что по

длине потока с ростом давления (пьезометрического напора) ско-

рости уменьшается и наоборот – с увеличением скорости умень-

шается давление.

17

Потери напора (удельной энергии) на единицу длины напор-

ного трубопровода называется гидравлическим (гидродинамиче-

ском) уклоном.

Падение пьезометрического напора (удельной потенциаль-

ной энергии) на единицу длины напорного трубопровода называ-

ется пьезометрическом уклоном.

Пьезометрический уклон может быть положительным и от-

рицательным.

Не нашли, что искали? Воспользуйтесь поиском по сайту: