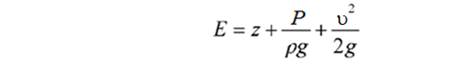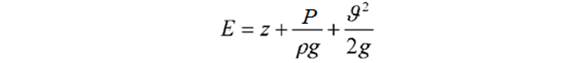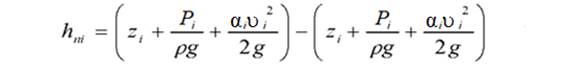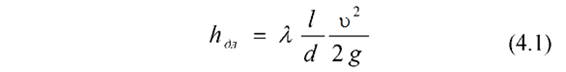Описание опытной установки

На характерных участках трубопровода, т.е. при переходе

труб от одного диаметра к другому, на конических участках ус-

тановлены пьезометры. Все пьезометры выведены на специаль-

ный щит. Вода в трубопровод подается из расходного бака. Рас-

ход измеряется при помощи мерного бака и регулируется уста-

новленным в конце трубопровода вентилем.

Порядок выполнения работы

1. До начала работы убедиться в том, что в пьезометрах от-

сутствует воздух и уровни воды в них одинаковы.

2. Открыть вентиль слива и определить время, в течение ко-

торого в мерный бак поступит 10 л воды.

3. Снять показания пьезометров.

4. От любого горизонтального уровня измерить и записать

расстояния z до точек установки пьезометров.

5. Определить расход воды, разделив объем воды 0,01 м³ на

время опыта.

6. Вычислить площади живого сечения ω для диаметров труб

в точках установки пьезометров.

7. Из уравнения неразрывности потока Q = ω υ для разных

сечений трубопровода определить средние скорости воды.

8. Подсчитать скоростные напоры υ² /2g.

9. По показаниям пьезометров и значениям скоростных напо-

ров подсчитать полные удельные энергии в сечениях

10. Определить потери энергии между сечениями

αi принять равным 1,0

11. На миллиметровой бумаге построить пьезометрическую и

напорную линии (рис. 3.2), для этого:

- в масштабе вычертить схему трубопровода переменного се-

чения с указанием местных сопротивлений, пьезометров и рас-

стояний;

- провести вертикальные линии в плоскости сечений, к кото-

рым подключены пьезометры, а также в плоскости сечений, сов-

падающих с местными сопротивлениями;

- на соответствующих вертикальных линиях откладываем

значения пьезометрических напоров и соединяя точки, получаем

пьезометрическую линию П-П;

- от линии П-П откладываем значения скоростных напоров и

получаем линию гидродинамического напора.

3.4. Контрольные вопросы

1. В чем заключается геометрический и энергетический смыс-

лы уравнения Бернулли?

2. Какие составляющие необходимо учитывать при построе-

нии пьезометрической и напорной линии?

3. Что представляет гидравлический и пьезометрический ук-

лоны?

РАБОТА 4. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ГИДРАВЛИЧЕСКОГ

ТРЕНИЯ

Цель работы– опытное определение коэффициента гидрав-

лического трения λ для различных зон гидравлических сопротив-

лений.

Теоретическое положение

При движении в трубопроводах и каналах часть энергии по-

тока расходуется на преодоление сопротивлений, обусловленных

трением жидкости о стенки трубопровода и трением между слоя-

ми внутри жидкости.

Потери напора по длине в трубах круглого сечения опреде-

ляются по формуле Дарси-Вейсбаха

а в открытых руслах (а также в трубах любой формы сечения)

по формуле:

где λ – коэффициент сопротивления по длине;

l и d – длина и диаметр трубопровода;

υ – средняя скорость потока;

g – ускорение свободного падения;

R – гидравлический радиус, равный отношению пло-

щади сечения ω к смоченному периметру х:

Диаметр гидравлический d 2 = 4 R.

Для труб круглого сечения гидравлический диаметр d 2 сов-

падает с геометрическим d, т.е. d 2 = d.

Для определения коэффициента λ предложен ряд формул,

учитывающих зависимость его от диаметра трубы d, шероховато-

сти стенок Δ и числа Рейнольдса Re.

Экспериментальными работами А. Никурадзе и А.П. Зегжда

установлено существование пяти зон сопротивлений (рис. 4.2):

1 – зона вязкого сопротивления. Наблюдается при ламинар-

ном режиме движения Re < 2320.

2 – зона перехода от ламинарного к турбулентному

2320 < Re < 4000.

3 – зона гладкостенного сопротивления. Турбулентные по-

токи состоят из пограничного слоя и турбулентного ядра. Погра-

ничный слой расположен непосредственно у стенок труб и со-

стоит из тонкого слоя жидкости с ламинарным движением тол-

щиной δ пл., называемого ламинарной пленкой и переходного слоя

(рис.4.1).

Толщина ламинарной пленки определяется:

Наблюдается 3-й режим при δ пл. > Δ и числах Рейнольдса

4000 < Re < 10 d/ Δ

4 – зона переходная от гладкостенного сопротивления к

квадратичному. Здесь выступы шероховатости начинают обна-

жаться и выходить за пределы ламинарной пленки.

10 d/ Δ < Re <560 d/ Δ

При ламинарном режиме коэффициент гидравлического

трения определяется по закону Пуазейля

Для турбулентного режима пользуются различными эмпи-

рическими зависимостями, полученными опытным путем.

Для гидравлических гладких труб (3 зона) определяется по

формуле Блазиуса

или П.К. Конакова

Для переходной области (4 зона) пользуются формулой А.Д.

Альтшуля

или Френкеля

В области квадратичных сопротивлений (5 зона) коэффици-

ент трения может быть определен по формуле Шифренсона

А для остальных и чугунных труб, бывших в эксплуатации

по формуле Ф.А. Шевелева

Рис. 4.1. График Никурадзе

Рис. 4.2. Схематическое изображение гидравлически гладкой (а) и

Не нашли, что искали? Воспользуйтесь поиском по сайту: