
|
|
Передачи коническими зубчатыми колесамиПередачи коническими зубчатыми колесами применяются когда необходимо передать крутящий момент под углом, обычно 900.
Элементы конического колеса показаны на рис.4.8. На рисунке обозначено: δ – угол делительного конуса; d – средний делительный диаметр; de – внешний делительный диаметр; de1 – внешний диаметр вершин зубьев; R – среднее конусное расстояние; Re – внешнее конусное расстояние; b – ширина зубчатого венца. У конических зубчатых колес модуль – величина переменная, поэтому прочностные расчеты проводят по Рис.4.8среднему модулю и, соответственно, по среднему конусному расстоянию R = Re – b/2 и среднему делительному диаметру d. Условие контактной прочности имеет вид
KH и [σ]H принимаются так же, как и для цилиндрических передач. При проектировочном расчете определяют внешний делительный диаметр колеса
ψbRe = b/Re= 0,285 – коэффициент ширины зубчатого венца. Далее задаются z1 ≈18…30; определяют z2 = z1*uи определяют внешний окружной модуль me = de2/ z2 и определяют все остальные геометрические параметры передачи. Необходимые для этого формулы и значенияпараметров приведены в литературе.
4.1.8 Пример выполнения чертежа зубчатого колеса (рис. 4.9).
Рис. 4.9 Трение
Трение – это совокупность явлений, возникающих в месте контакта двух тел, которые препятствуют их любому относительному движению. Различают два вида трения: трение покоя (нет относительного движения тел); трение движения (есть относительное движение тел). Трение движения разделяется на трение скольжения и трение качения. Сила трения – это сила, препятствующая относительному перемещению двух тел при трении. Между силой трения Fи нормальной составляющей реакций на внешнее воздействие Nсуществует зависимость F = f* N, (4.18) где f – коэффициент трения, определяемый опытным путем и зависящий от условий контакта тел. Вы наверняка замечали, что сдвинуть груз с места труднее, чем двигать его после трогания с места. Поэтому различают силу трения покоя Fпи силу трения движения F. Соответственно, следует различать коэффициент трения покоя f п = Fп/ N (4.19) и коэффициент трения движения f = F/ N (4.20) Как правило f п > f Рассмотрим перемещение груза по горизонтальной (рис.4.10, а) и наклонной (рис.4.10, б, в) плоскостям.
Рис. 4.10 Из рис.4.10, а) видим, что сила трения F отклоняет реакцию Nна угол φ. Чтобы передвинуть груз надо приложить силу P ≥ F . f = F/ N = tq φ. φ = arctq(f) (4.21) – называется углом трения. При перемещении груза по наклонной плоскости (рис.4.10, б, в) реакцию Fа = Q отклоняет не только сила трения, но и составляющая силы тяжести, вызванная наклоном груза. В результате возникает сила сопротивленияFt = Fa*tq(φ + α)– при движении вверх;Ft = Fa*tq(φ - α)– при движении вниз. Из рисунка 4.10, в) видим, что при отсутствии внешней силы P, пока угол трения φ > αгруз не будет самопроизвольно перемещаться вниз. Условие φ > α называется условием самоторможения. При φ = αгруз находится в состоянии безразличного равновесия. Коэффициент трения скольжения зависит от многих факторов: материалов тел; вида и характера смазки; конфигурации тел; шероховатости контактирующих поверхностей и др. С учетом этих факторов общее понятие – коэффициент трения, заменяют понятием – приведенный коэффициент трения. А в формулах заменяют f = tq φ на f ' = tq φ',где φ' – приведенный угол трения.
При качении круглого тела по поверхности, из за деформации контактирующих тел, нормальная составляющая сил N смещается в сторону движения на величину k (рис.4.11), называемую коэффициентом трения качения и имеющую размерность см. При этом возникает момент трения равный Tk = N*k (4.22) Рис. 4.11 Для стального колеса, катящегося по рельсу k ≈0,005 см; для ролика или шарика, катящегося по закаленной дорожке подшипника качения, k= 0,0005…0,001 см. В механизмах и машинах потери на трение качения значительно меньше, чем на трение скольжения. Поэтому, там, где это возможно, заменяют трение скольжения на трение качения. Например, в некоторых кулачковых механизмах, чтобы убрать трение скольжения толкателя по кулачку, на конце толкателя устанавливают ролик. Приведенные выше понятия и формулы нужны при расчете червячных передач; фрикционных передач и механизмов; резьбовых соединений и др.
Червячные передачи
Рис. 4.12окружности червяка. У червяка нет зубьев, у него есть винтовые нарезки (винтовые линии). Количество винтовых линий (при взгляде с торца червяка) называется числом заходов червяка z1. В червячных редукторах обычно z1 = 1 или 2. Передаточное отношение равно u = z2/ z1, где z2 – число зубьев червячного колеса. Основные достоинства червячных передач: большое передаточное число при малых габаритах передачи (в стандартных редукторах u = 8…100); возможность самоторможения (используется в грузоподъемных механизмах); плавность и бесшумность работы.
Материалы червячных передач: червяк стальной закаленный и желательно шлифованный; червячное колесо или его венец – бронзовые, в крупногабаритных передачах – чугунные. На рис. 4.13 показана развертка винтовой линии двухзаходного червяка по делительной окружности. На рисунке приняты обозначения: p – шаг червяка (p = π*m); px – ход винтовой линии; d – делительный диаметр червяка; γ – делительный угол подъема витка червяка. Очевидно соотношение px = p* z1 = π* m* z1 Видим px/ (πd) = tq γ, отсюда , заменяя px = π* m* z1, получаем d = m* z1/ tq γ = q* m . Параметр q = z1/tq γ (4.23) называется коэффициентом диаметра червяка. Эта Рис. 4.13величина стандартизована. ГОСТ 2144-76 рекомендует ряд значений q в сочетании с рядом модулей. Остальные параметры (элементы) передачи определяются аналогично зубчатым передачам. da1 = d1 + 2m = m*( q +2); df1 = d1 – 2,4m = m*( q – 2,4);длину нарезанной части червяка b1 принимают b1 ≥ (11 + 0,06 z2). d2 = m* z2; da2 = d2 + 2 m = m*( z2 + 2); df2 = d2 – 2,4m = m*( z2 – 2,4);наибольший диаметр червячного колеса определяют по формуле dam2 ≤ da2 + 6 m/( z1 +2);ширина венца колеса b2 ≤ 0,75 da1. Коэффициент полезного действия червячного редуктора с учетом потерь в зацеплении и в опорах определяется по формуле η = (0,95…0,96)*tq γ/[tq(γ + φ')] , (4.24) где φ' – приведенный угол трения. КПД возрастает с увеличением числа заходов червяка, поскольку увеличивается γ.Приведенный угол трения очень сильно зависит от скорости скольжения
где v1 = 0,5ω1*d1*10 –3 и v2 = 0,5ω2*d2*10 –3 – окружные скорости червяка и колеса, м/с; ω1 и ω2 – угловые скорости червяка и колеса, рад/с. При увеличении скорости скольжения от 0,01 м/с до 15 м/с приведенный угол трения уменьшается от 60 до 10, а следовательно повышается КПД. В червячной передаче наиболее слабым звеном является колесо, поэтому прочностные расчеты проводят именно червячного колеса. Расчеты выполняются в такой последовательности. Известно: Т2; u = z2/ z1;принимаете сами z1и q; выбираете материал колеса и по рекомендациям или задавшись коэффициентом запаса прочности определяете [σ]H. Определяете межосевое расстояние по формуле
где Т2 – крутящий момент на валу колеса, Н*мм (определяется из кинематического расчета). Учитывая, что aw = (d1 + d2) / 2 = m*( q + z2)/2, (4.27) m = 2 aw/*( q + z2) (4.28) Затем определяете все остальные параметры (элементы) передачи по формулам, приведенным выше.
В заключение проводим проверку выполнения условия прочности на изгиб σF = 1,5YF*KFβ*KFv*cos γ*T2/(d1*d2*m) ≤ [σ]F (4.29) Все коэффициенты и допустимое напряжение берем из литературы. В случае не выполнения условия прочности, определяем модуль по формуле
Фрикционные передачи Во фрикционных передачах движение от ведущего звена к ведомому передается за счет сил трения, возникающих между прижатыми друг к другу колесами. Различают передачи с постоянным передаточным отношением и с переменным передаточным отношением. Последние называются фрикционные вариаторы.
По этому рисунку составим основы теории фрикционных передач, отметим из достоинства и недостатки. Ведущий каток передает крутящий момент Рис. 4.14 Т1 = Р*d1/2.В месте касания катков возникает сила трения F = Q*f, где f – коэффициент трения скольжения. Для предотвращения проскальзывания катков необходим некоторый запас надежности сцепления. k = F/P = Q* f* d1/ 2Т1 > 1, откуда необходимое условие прижатия катков Q = 2 k* Т1/( f* d1) = k*P/f (4.31) k– коэффициент надежности сцепления. Для силовых передач принимаютk =1,25…1,5;в приборах k = 3 и более. Для пары сталь – сталь f= 0,05 при работе со смазкой; f= 0,1…0,15 при работе всухую. Предположим, что необходима сила Р = 100 Н. Приняли f= 0,12; k =1,3. Тогда Q = k*P/f = 1,3*100/0,12 = 1083 Н. То есть чтобы получить силу всего 100Н необходимо прижимать катки силой 1083 Н. Это существенный недостаток фрикционных передач с линейным или точечным контактом звеньев. К достоинствам фрикционных передач можно отнести: простоту конструкций; плавность и бесшумность работы; предохранение от поломок при перегрузках (будет происходить проскальзывание). Расчет элементов передачи проводят, как правило, на контактную прочность по формуле Герца (4.4), аналогично расчету зубчатых колес. Поэтому здесь мы не будем останавливаться на этом вопросе. Передаточное отношение. u1-2 = ω1/ω2 = d2/[d1*(1 – ξ)], (4.32) где ξ= 0,002…0,05 – коэффициент, учитывающий проскальзывание в передаче (определяется экспериментально). Довольно широкий диапазон значений говорит о том, что этот коэффициент приблизительный и может меняться в процессе эксплуатации передачи. Фрикционные вариаторы На рис. 4.15 приведены три схемы вариаторов. Лобовой вариатор (рис. 4.15, а). В нем при постоянном R1 меняется R2, поэтому u = R2/ R1 # const.Вариатор с конусными барабанами и промежуточным роликом (рис. 4.15, б), который перемещается вдоль своей оси. При этом R1 и R2 изменяются. Соответственно u = R2/ R1 # const.
u = R2/ R1 # const. Все показанные вариаторы могут работать как в режиме понижения оборотов (редуктор) при R2 > R1 , так и в режиме повышения оборотов (мультипликатор) при R2 < R1. Рис.4.15Вариаторы по схемам (рис. 4.15, а; б) не могут передавать большие крутящие моменты, поэтому применяются в основном в приборах и других маломощных механизмах. Клиноременной вариатор, имея достоинства обычной клиноременной передачи и способный плавно регулировать скорость на ведомом валу, применяется в силовых механизмах и машинах. В частности, на снегоходе «Буран» вместо коробки передач установлен клиноременной вариатор.
Ременные передачи
Плоскоременные передачи Схема плоскоременной передачи показана на рис. 4.16.
Выпускаются прорезиненные ремни трех типов: А – нарезные с резиновыми прослойками, рекомендуются при скорости до 30 м/с; Б – послойно завернутые, с прослойками или без них, рекомендуемая Рис. 4.16скорость до 20 м/с; В – спирально-завернутые, без прослоек, скорость до 15 м/с. Количество прокладок от 2-х до 8-ми. Толщина одной прокладки 1,25 мм; прокладки с прослойкой – 1,5 мм. Ширина ремней b = 20…400 мм.
Методика расчета плоскоременной передачи. Исходными данными являются: передаваемая мощность N, Вт; частота вращения ведущего шкива n1, об/мин или скорость ремня v, м/с; передаточное отношение u = n1/ n2. Скорость ремня зависит от диаметра шкива и оборотов v = πD1* n1/60. Поэтому вначале определяют диаметр ведущего шкива по формуле
Находят диаметр ведомого шкива с учетом относительного скольжения ε=0,01
Определяют скорость ремня v = πD1* n1/60. Определяют окружное усилие Р = N/ v Допускаемое напряжение (удельное окружное усилие на единицу площади поперечного сечения ремня) определяется по формуле [k] = k0C0CαCvCp (4.34) Значения k0 при v = 10 м/с; α = 1800 (угол обхвата шкива ремнем); σ0 = 1,8 МПа (напряжение от предварительного натяжения), приведены в Таблица 4.4
таблице 4.4. Коэффициент C0 учитывает расположение передачи. Для горизонтальных и наклонных до 600 передач C0 = 1; при наклоне 60…800 C0 = 0,9; при наклоне 80…900 C0 = 0,8. Коэффициент Cαучитывает влияние угла обхвата α10, который зависит от межосевого расстояния а.Поэтому, предварительно задают а = 2(D1 + D2).Угол обхвата на меньшем шкиве определяется по формуле α10 = 1800 - 60*( D2 - D1)/ а (4.35) Угол α10 должен быть ≥ 1500. Коэффициент Cα = 1 – 0,003*(180 - α10). Коэффициент Cv учитывает влияние скорости Cv = 1,04 – 0,0004 v2. Коэффициент Cp учитывает условия эксплуатации передачи. При спокойной работе и пусковых нагрузках не выше 120% от номинальной Cp = 1. При умеренных колебаниях нагрузки и пусковой до 150% Cp = 0,9. При значительных колебаниях нагрузки и пусковой до 200% Cp = 0,8. При ударных нагрузках и пусковой до 300% (молоты, дробилки и пр.) Cp = 0,7. При двухсменной работе Cp брать на 0,1 меньше; при трехсменной – на 0,2 меньше. После определения [k] находят необходимую площадь сечения ремня по формуле b*δ = Р/[k] (4.36) Из условия δ/ D1 ≤ 1/40или ≤ 1/50и, учитывая, что толщина прокладок (без прослоек) 1,25мм, с прослойками 1,5 мм, находят δ и число прокладок. Затем определяют ширину ремня b.
Длина ремня определяется по формуле L = 2а + π*( D1 + D2)/2 + (D2 - D1)2/4а (4.37) Силы, действующие в передаче: предварительное натяжение каждой ветви S0 = σ0*b* δ(σ0 =1,8 МПа); натяжение ведущей ветви S1 = S0 + Р/2;натяжение ведомой ветви S1 = S0 - Р/2;давление на вал Q = 2 S0*sin(α1/2). Максимальное начальное натяжение (с учетом последующего ослабления) принимают: Qmax = 1,5Q. Полученные значения параметров ремня (длину, ширину, толщину и число прокладок) округляют до ближайших значений, взятых из каталогов фирм изготовителей или из ГОСТа на данный тип ремней. При окончательном выборе ремня следует иметь в виду, что более тонкие ремни (соответственно более широкие) обладают большей долговечностью, поскольку в них возникают меньшие по величине напряжения изгиба при огибании шкивов. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Например, валы рукояток управления в станках зачастую расположены перпендикулярно силовым винтовым передачам; карданный вал автомобиля перпендикулярен полуосям моста и др.
Например, валы рукояток управления в станках зачастую расположены перпендикулярно силовым винтовым передачам; карданный вал автомобиля перпендикулярен полуосям моста и др. (4.16)
(4.16) (4.17)
(4.17)

 Трение качения
Трение качения Червячные передачи (рис. 4.12) относятся к числу зубчато-винтовых, имеющих характерные черты зубчатых и винтовых передач. Они состоят из червяка 1 и червячного колеса 2. Червяк представляет собой винт с резьбой близкой к трапецеидальной. Червячное колесо – это косозубое цилиндрическое колесо, особенностью которого является огибание зубьями колеса части
Червячные передачи (рис. 4.12) относятся к числу зубчато-винтовых, имеющих характерные черты зубчатых и винтовых передач. Они состоят из червяка 1 и червячного колеса 2. Червяк представляет собой винт с резьбой близкой к трапецеидальной. Червячное колесо – это косозубое цилиндрическое колесо, особенностью которого является огибание зубьями колеса части Недостатки: низкий КПД (0,7…0,85); необходимость применения для колеса дорогостоящих антифрикционных материалов.
Недостатки: низкий КПД (0,7…0,85); необходимость применения для колеса дорогостоящих антифрикционных материалов. , (4.25)
, (4.25) , (4.26)
, (4.26) (4.30)
(4.30)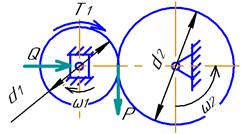 На рис.4.14 показана схема фрикционной передачи с постоянным передаточным отношением.
На рис.4.14 показана схема фрикционной передачи с постоянным передаточным отношением. На рис. 4.15, в) показан клиноременной вариатор с подвижными конусами. Перемещение конусов ведомого звена осуществляется с помощью винтового механизма. Постоянную натяжку ремня выполняет пружина, установленная на ведущем звене. При этом R1 и R2 изменяются.
На рис. 4.15, в) показан клиноременной вариатор с подвижными конусами. Перемещение конусов ведомого звена осуществляется с помощью винтового механизма. Постоянную натяжку ремня выполняет пружина, установленная на ведущем звене. При этом R1 и R2 изменяются. В плоскоременных передачах применяют ремни: прорезиненные; хлопчатобумажные; кожаные. Наиболее распространены прорезиненные ремни. Методика подбора ремней однотипна.
В плоскоременных передачах применяют ремни: прорезиненные; хлопчатобумажные; кожаные. Наиболее распространены прорезиненные ремни. Методика подбора ремней однотипна. , мм (4.33)
, мм (4.33)