
|
|
I I I Основы теории механизмов и машин (ТММ)ТММ– это наука, изучающая структуру, кинематику и динамику механизмов и машин при их анализе и синтезе. Ввиду краткости нашего курса, остановимся только на структурном и кинематическом исследовании механизмов. Целью этих исследований является изучение строения механизмов и анализ движения их звеньев независимо от сил, вызывающих это движение. В ТММ изучаются идеальные механизмы: абсолютно не деформируемые; не имеющие зазоров в подвижных соединениях. Основные положения ТММ являются общими для механизмов различного назначения. Они используются на первой стадии проектирования, то есть при разработке схемы механизма и расчете его кинематических и динамических параметров. После выполнения этой стадии проектирования Вы видите «скелет» вашего будущего изделия, заложенные в него идеи. В дальнейшем проводите реализацию Ваших идей в виде конструкторской документации и в виде реальных изделий.
3.1 Структурный анализ механизмов
3.1.1 Основные понятия и определения
Деталь – отдельная, неделимая часть механизма (деталь разобрать на части нельзя). Звено – деталь или несколько деталей, соединенных между собой неподвижно. Кинематическая пара (КП) – подвижное соединение двух звеньев. КП не материальная величина, она характеризует соединение двух звеньев, находящихся в непосредственном соприкосновении. Элемент КП – точка, линия или поверхность, по которым одно звено соприкасается с другим. Если элементом КП является точка или линия – это высшая КП, если поверхность – это низшая КП. По характеру движения звеньев КП бывают: вращательные, поступательные, с винтовым движением. По виду соприкасающихся поверхностей КП бывают: плоскостные, цилиндрические, сферические и др. Класс КП определяется числом ограничений движения или числом наложенных связей S. Всего 6 степеней свободы. Обозначим Н – число степеней свободы. Можно записать Н + S = 6 или Н = 6 – S, или S = 6 – Н Зачастую бывает проще определить сколько степеней свободы у звена осталось, чем сколько наложено связей. Например, сколько степеней свободы у двери или форточки – одна. Что является элементом КП – поверхность (зазоров нет). Какой характер движения – вращение. Следовательно – это низшая, вращательная КП 5-го класса. Достаточно часто приходится сталкиваться и с высшими КП, например: контакт зубчатых колес; цилиндр катится по плоскости; цилиндр по цилиндру; толкатель по кулачку и др. Такое соединение показано на рис.3.1.
Кинематическая цепь – система звеньев, соединенных кинематическими парами. Механизм – кинематическая цепь, в которой при заданном движении одного или нескольких ведущих звеньев относительно неподвижного Рис.3.1 звена (стойки), все остальные звенья (ведомые) совершают определенное движение. Ведомое звено, совершающее движение, ради которого создан механизм, называется рабочим звеном. При составлении схем механизмов и других кинематических цепей применяются условные изображения согласно ГОСТ 2.770-68. При этом кинематические пары обозначаются заглавными буквами, а звенья – цифрами. Ведущее звено указывается стрелкой. Неподвижное звено (стойка) обозначается подштриховкой около кинематических пар. Различают понятия структурная схема и кинематическая схема механизма. Кинематические схемы механизмов отличаются от структурных тем, что должны выполняться строго в масштабе и при заданном положении ведущего звена. В действительности это требование мало кто соблюдает. Возьмите паспорт любого станка или бытового прибора. Написано – Кинематическая схема - , но ни о каком масштабе речи не идет. Чтобы не нарушать ГОСТ 2.770-68, будем называть просто – схема механизма. В шарнирно-рычажных механизмах звенья имеют свои названия: вращающееся звено – кривошип; качающееся звено – коромысло;совершающее плоскопараллельное движение – шатун; поступательное движение – ползун; звенья, образующие поступательную пару с ползунами – направляющие; подвижные направляющие – кулисы. Валиками называются детали вращающихся звеньев, передающие крутящий момент. Ось – цилиндрическая деталь, которая охватывается элементами других звеньев и образует с ними вращательные пары – шарниры. Оси не передают крутящий момент.
3.1.2 Степень подвижности механизма
Степенью подвижности механизма называется число степеней свободы механизма относительно неподвижного звена (стойки). Степень подвижности плоского механизма (все звенья движутся в параллельных плоскостях) определяется по формуле П.Л. Чебышева W = 3n - 2P5 – P4, где n – число подвижных звеньев; P5 – число КП 5-го класса; P4 – число КП 4-го класса.
Рис. 3.2 Схемы механизмов На рис.3.2 показано несколько схем механизмов. Запишем названия звеньев, дадим характеристику кинематическим парам и определим степень подвижности каждого механизма. Схема 1: 1 – стойка; 11 – направляющая; 2 – кривошип; 3 – шатун; 4 – ползун; А, В, С – низшие вращательные КП 5-го класса; Д – низшая поступательная КП 5-го класса. W = 3n - 2P5 – P4 = 3*3 – 2*4 = 1. Схема 2: 1 – стойка; 2 – кривошип; 3 – кулиса; 4 – коромысло; А, С, Д – низшие вращательные КП 5-го класса; В – низшая поступательная КП 5-го класса. W = 3n - 2P5 – P4 = 3*3 – 2*4 = 1. Схема 3: 1 – направляющая; 2, 4 – ползуны (толкатели); 3 – коромысло; А, Е – низшие поступательные КП 5-го класса; С – низшая вращательная КП 5-го класса; В, Д – высшие КП 4-го класса. W = 3n - 2P5 – P4 = 3*3 – 2*3 - 2 = 1. Схема 4: 1 – стойка; 11 направляющая; 2 – кулачок; 3 – ролик; 4 – ползун (толкатель); А, С – низшие вращательные КП 5-го класса; Д – низшая поступательная КП 5-го класса; В – высшая КП 4-го класса. W = 3n - 2P5 – P4 = 3*3 – 2*3 - 1 = 2. Схема 5: 1 – стойка; 11 направляющая; 2 – кулачок; 3 – ползун (толкатель); А - низшая вращательная КП 5-го класса; С – низшая поступательная КП 5-го класса; В – высшая КП 4-го класса. W = 3n - 2P5 – P4 = 3*2 – 2*2 - 1 = 1. На схемах 4 и 5 показаны кулачковые механизмы, имеющие, соответственно 2 и 1 степени подвижности, хотя очевидно, что толкатели этих механизмов имеют одну степень свободы. Лишняя степень подвижности механизма (схема 4) вызвана наличием звена 3 (ролика), которое не влияет на закон движения рабочего звена (толкателя). При структурном и кинематическом анализах механизмов такие звенья удаляют из схемы механизма.
3.1.3 Замена высших кинематических пар низшими
При структурном, кинематическом и силовом исследованиях механизмов в некоторых случаях целесообразно заменить механизм с высшими парами 4-го класса эквивалентным механизмом с низшими парами 5-го класса. При этом число степеней свободы и мгновенное движение звеньев у эквивалентного заменяющего механизма должно быть таким же, как у заменяемого механизма.
Рис. 3.3 кривошипно-кулисным механизмом 1, 4, 5, 3. Высшая пара В заменена низшими парами Д, Е. Алгоритм замены высших кинематических пар на низшие следующий: 1) через точку контакта звеньев в высшей КП проводится нормаль; 2) на нормали на расстояниях радиусов кривизны (R1 и R2, рис.3.3, а) ставятся низшие КП; 3) полученные КП соединяются звеньями с уже бывшими в механизме низшими КП.
3.1.4 Структурный синтез и анализ механизмов
Структурный синтез механизмов является начальной стадией составления схемы механизма, удовлетворяющего заданным условиям. Исходными данными обычно являются виды движения ведущего и рабочего звеньев механизма. Если элементарный трех- или четырехзвенный механизм не решает задачу требуемого преобразования движения, схема механизма составляется путем последовательного соединения нескольких элементарных механизмов. Основные принципы структурного синтеза и анализа механизмов с КП 5-го класса и классификацию таких механизмов впервые предложил русский ученый Л.В. Ассур в 1914году, а развил идеи Л.В. Ассура академик И.И. Артоболевский. Согласно предложенной классификации механизмы объединяются в классы от первого и выше по структурным признакам. Механизм первого класса состоит из ведущего звена и стойки, соединенных кинематической парой 5-го класса. Механизмы более высоких классов образуются последовательным присоединением к механизму первого класса кинематических цепей, не изменяющих степени подвижности исходного механизма, то есть имеющих степень подвижности, равную нулю. Такая кинематическая цепь называется структурной группой. Поскольку в структурную группу входят только КП 5-го класса, а степень подвижности группы равна нулю, то можно записать W = 3n - 2P5 = 0, откуда P5 = 3/2 n. Следовательно, в структурную группу может входить только четное число звеньев, поскольку P5 может быть только целым числом. Структурные группы различают по классу и порядку. Группа 2-го класса и 2-го порядка состоит из двух звеньев и трех КП. Класс группы (выше 2-го) определяется числом внутренних КП, образующих подвижный замкнутый контур из наибольшего числа звеньев группы. Порядок группы определяется числом свободных элементов звеньев, которыми группа присоединяется к механизму. На рис.3.4 показан механизм 1-го класса, а так же структурные группы 2-го и 3-го классов. В результате структурного синтеза (присоединение структурных групп к механизму 1-го класса) получены четырехзвенные механизмы 2-го класса и шестизвенный механизм 3-го класса (рис.3.4). При структурном анализе определяется степень подвижности механизма и разложение его кинематической цепи на структурные группы и ведущие звенья. При этом удаляются лишние степени свободы (если они есть) и пассивные связи (при их наличии).
Рис. 3.4
3.2 Кинематический анализ механизмов
Целью кинематического анализа является изучение движения звеньев механизма независимо от действующих на них сил. При этом принимаются допущения: звенья абсолютно жесткие и в кинематических парах отсутствуют зазоры. Решаются следующие основные задачи: а) определение положений звеньев и построение траекторий движения отдельных точек или звеньев в целом; б) нахождение линейных скоростей точек механизма и угловых скоростей звеньев; в) определение линейных ускорений точек механизма и угловых ускорений звеньев. Исходными данными являются: кинематическая схема механизма; размеры всех звеньев; законы движения ведущих звеньев. При кинематическом анализе механизмов используются аналитические, графоаналитические и графические методы. Обычно рассматривается полный цикл движения механизма. Результаты кинематического анализа позволяют при необходимости скорректировать схему механизма, кроме того, они необходимы для решения задач динамики механизма.
3.2.1 Определение положений и перемещений звеньев механизма
Решение задачи проведем графическим и аналитическим методами. В качестве примера возьмем кривошипно-ползунный механизм. Дано: длина кривошипа r = 150 мм; длина шатуна l = 450 мм; ведущий кривошип (ω = const.) Положение кривошипа задается углом φ. Цикл движения такого механизма осуществляется за один полный оборот кривошипа – период цикла Т = 60/n = 2π/ω, с. Где n - число оборотов в минуту; ω – угловая скорость, с-1. При этом φ = 2π, рад. Вычерчиваем кинематическую схему механизма в выбранном масштабе (рис.3.5). На рис.3.5 принят масштаб 1:10. Строим схему механизма в восьми положениях кривошипа (чем больше положений механизма, тем выше точность полученных результатов). Отмечаем положение ползуна (рабочее звено). По полученным данным строим график зависимости перемещения точки В ползуна от угла поворота кривошипа φ (SВ = f(φ)). Этот график называется кинематической диаграммой перемещений точки В.
Аналитический метод Перемещение ползуна отсчитывается от крайнего правого положения (рис.3.5). Анализируя рисунок, можно записать уравнения
r*sin φ = l*sin β Обозначив r/ l = λ, можно записать β = arcsin(λ* sin φ). Следовательно, для каждого угла φ не сложно определить соответствующий угол β, а затем решить первое уравнение системы (3.1). При Рис. 3.5 этом точность результатов будет определяться только заданной точностью расчетов. В [1] приведена приближенная формула для определения перемещений ползуна S = r*(1 - cos φ + sin2 φ* λ /2) (3.2)
3.2.2 Определение скоростей и ускорений точек и звеньев механизма
Скорости и ускорения ведомых звеньев механизма могут быть определены методами планов, кинематических диаграмм и аналитическими. Во всех случаях в качестве исходных должны быть известны: схема механизма при определенном положении ведущего звена, его скорость и ускорение.
Рассмотрим применение указанных методов на примере кривошипно-ползунного механизма (рис.3.5) при φ = 45о и n = 1200 об/мин, соответственно ω = π*n/30 = 125,7 с-1. План скоростей (ускорений) механизма. Планом скоростей (ускорений) механизма называется фигура, образованная векторами скоростей (ускорений) точек звеньев при заданном положении механизма.
Известно По величине VАО = ω* r = 125,7*0,15 = 18,9 м/с. Выбираем масштаб построения, например, 1м/(с*мм). Отмечаем какую-нибудь точку в качестве полюса Р при построении плана скоростей (рис.3.6). От полюса откладываем вектор Рис. 3.6 перпендикулярно АО. Вектор скорости точки В находим путем графического решения уравнения
Построение плана ускорений (рис.3.7) Ускорение точки А равно = 125,72*0,15 = 2370 м/с2. Касательное ускорение atАО = ε* r = 0, так как угловое ускорение ε = 0, поскольку ω = const. Рис. 3.7 Выбираем масштаб построения, например, 100м/(с2*мм). Откладываем от полюса ра вектор aВ = 1740 м/с2; atВА = 1650 м/с2.
Метод кинематических диаграмм (рис.3.8) Метод кинематических диаграмм – это графический метод. Он включает в себя графическое дифференци-рование сначала графика перемещений, а затем графика скорости. При этом кривые перемещений и скорости заменяются ломаной линией. Значение средней скорости на элементарном участке пути можно выразить в виде
µS – масштаб перемещения. µt – масштаб времени. В нашем случае µS = 0,01 м/мм; µ t = 0,000625 с/мм. Масштаб скорости равен µV = µS/(µ t*HV) = 0,01/(0,000625*30) = = 0,533 м/(с*мм). Масштаб ускорения равен µа = µV/(µ t* Hа) = 0,533/(0,000625*30) = = 28,44 м/(с2*мм). Порядок построения диаграммы скорости. На расстоянии HV (20…40мм) ставится точка О – полюс построения. Из полюса проводятся прямые, параллельные отрезкам ломаной линии графика перемещения, до пересечения оси ординат. Ординаты переносятся на график скорости в середину соответствующих участков. По полученным точкам проводится кривая – это и есть диаграмма скорости. Диаграмма ускорения строится аналогично, только исходным графиком становится диаграмма скорости, замененная ломаной линией.
Для указания численных значений скорости и ускорения рассчитывается масштаб построения, как показано выше. Скорости и ускорения ползуна можно определить и аналитическим способом, путем последовательного дифференцирования приближенного уравнения (3.2).
Знание скоростей и ускорений звеньев механизма необходимо для динамического анализа механизма, в частности, для определения сил инерции, которые могут при больших ускорениях (как в нашем случае) многократно превышать статические нагрузки, например, вес звена. Ввиду краткости нашего курса, мы не проводим силовое исследование механизмов, но Вы самостоятельно можете ознакомиться с ним по литературе, в частности, рекомендованной в этом разделе. В теории механизмов и машин рассматриваются вопросы геометрии зубчатого зацепления, а так же вопросы трения в кинематических парах. Мы тоже рассмотрим эти вопросы, но в разделе « детали машин », применительно к конкретным случаям и задачам.
Литература
1. Первицкий Ю.Д. Расчет и конструирование точных механизмов. – Л.: Машиностроение, 1976. – 456 с. 2. Заблонский К.И. Прикладная механика. – Киев : Вища школа, 1984. – 280 с. 3. Королев П.В. Теория механизмов и машин. Конспект лекций. – Иркутск : Издательство ИрГТУ, 2001. – 104 с.
IV Детали машин Курс «Детали машин» завершает цикл общеинженерных дисциплин и одновременно является первым из расчетно-конструкторских курсов, в котором изучают основы проектирования машин и механизмов. В курсе изучают детали (узлы) машин общего назначения, то есть такие, которые встречаются во всех машинах и механизмах или в большинстве из них. К таким деталям (узлам) относятся: передачи (зубчатые, червячные, фрикционные, гибкой связью); соединения (разъемные, не разъемные); валы, оси; подшипники качения и скольжения; муфты; пружины. Этот перечень говорит об объеме курса. Естественно, что по курсу имеется достаточно много литературы, как учебной, так и вспомогательной (различные справочники, атласы конструкций и др.). В нашем курсе «Прикладная механика» дисциплина «Детали машин» входит всего лишь заключительным разделом. Очевидно, что мы не сможем «объять необъятное». Сконцентрируем наше внимание на методике элементарных расчетов и возможности практического (прикладного) применения полученных знаний.
Зубчатые передачи. Элементы зубчатых колес. В паре зубчатого зацепления колесо с меньшим числом зубьев обычно называют шестерней, с большим – зубчатым колесом. Большинство зубчатых колес имеют эвольвентный профиль зуба.
Основные геометрические параметры (элементы) зубчатых колес показаны на рис.4.1. Индекс 1 относится к шестерне, индекс 2 – к колесу. Рис. 4.1 d1, d2 – делительные диаметры; da1, da2 – диаметры вершин зубьев; df1, df2 – диаметры впадин зубьев; a – межосевое расстояние;b1 – ширина шестерни; b2 – ширина колеса; ha – высота головки зуба; hf – высота ножки зуба; s – толщина зуба; e – ширина впадины; pn – нормальный шаг зубьев; z1, z2 – числа зубьев. Длина делительной окружности равна πd, с другой стороны она равна pn*z, следовательно d = (pn/π)* z. Величина m = pn/πназывается нормальным модулем или просто модулем зубчатого колеса. Модуль является основным, самым главным параметром зубчатого колеса, все остальные зависят от него. Модуль – величина стандартизованная, то есть существует стандартный ряд модулей, отступление от которого не допускается, иначе колесо не будет нарезано, поскольку весь зуборезный инструмент модульный. Как только определился модуль, все остальные элементы приобретают вид: d = m* z; ha = m; hf = 1,25 m; da = d + 2 ha = m*( z + 2); df = d - 2 hf = m*( z – 2,5); pn = m*π; s ≈ e = pn/2 = m*π/2; a = (d1 + d2)/2 = m*( z1 + z2)/2; b2 = ψba* a = ψba* m*( z1 + z2)/2,где ψba = b2/ a – рекомендуемая величина. Ширина шестерниb1берется большеширины колеса на 2…10 мм с тем, чтобы даже при небольшом осевом смещении в процессе сборки или эксплуатации колесо находилось в зацеплении с шестерней по всей ширине. То есть b1 = b2 + (2…10) = ψba* m*( z1 + z2)/2 + (2…10) . Видим, что все геометрические параметры (элементы) зубчатых колес зависят от модуля. Все, приведенные выше данные, относятся к прямозубым колесам. Для косозубых цилиндрических колес (рис.4.2) нужно учитывать угол наклона зубьев β. На рис.4.2 зубья условно срезаны до делительной окружности.
Подставив в формулы параметров (кроме haи hf) вместо m - mt,получим размеры элементов Рис.4.2косозубой передачи, в частности d = m* z/ cosβ; da = m*z / cosβ + 2 m; df = m*z / cosβ – 2,5 m. ha = m и hf = 1,25 m не зависят от вида передачи (прямозубая или косозубая). Практические способы определения модуля. В инженерной практике не редки случаи, когда возникает необходимость определения модуля вышедшей из строя шестерни с тем, чтобы изготовить новую шестерню. Применяется два способа: а) измеряют окружной шаг и угол наклона зубьев β (если шестерня косозубая); б) измеряют диаметр вершин зубьев. Определяют модуль: а) m = pt * cosβ/ π;б) m = da/( z / cosβ + 2). Полученные значения модуля округляют до ближайшего стандартного значения. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 В соединении присутствуют две составляющие относительного движения, то есть две степени свободы. Элементом КП является линия. Следовательно – это высшая КП 4-го класса.
В соединении присутствуют две составляющие относительного движения, то есть две степени свободы. Элементом КП является линия. Следовательно – это высшая КП 4-го класса.
 На рис.3.3, а) показана замена кулачкового механизма, состоящего из звеньев 1, 2, 3, шарнирным четырехзванником, составленного из звеньев 1, 4, 5, 6. Высшая кинематическая пара В заменена низшими парами Д, Е. На рис.3.3, б) кулачковый механизм 1, 2, 3 заменен
На рис.3.3, а) показана замена кулачкового механизма, состоящего из звеньев 1, 2, 3, шарнирным четырехзванником, составленного из звеньев 1, 4, 5, 6. Высшая кинематическая пара В заменена низшими парами Д, Е. На рис.3.3, б) кулачковый механизм 1, 2, 3 заменен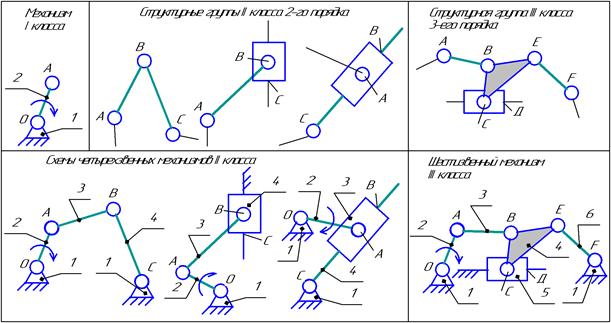

 S=(r+l)–(r*cosφ+l*cosβ) (3.1)
S=(r+l)–(r*cosφ+l*cosβ) (3.1) Построение плана скоростей
Построение плана скоростей 
 ,
, Известно направление векторов. Вектор
Известно направление векторов. Вектор  лежит на горизонтальной прямой, а вектор
лежит на горизонтальной прямой, а вектор 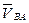 перпендикулярен ВА. Из полюса и конца вектора
перпендикулярен ВА. Из полюса и конца вектора  проводим соответствующие прямые и замыкаем векторное уравнение. Замеряем расстояние Pb и ba и, с учетом масштаба, находим
проводим соответствующие прямые и замыкаем векторное уравнение. Замеряем расстояние Pb и ba и, с учетом масштаба, находим VВ = 16,6 м/с, VВА = 13,8 м/с.
VВ = 16,6 м/с, VВА = 13,8 м/с.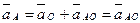 , поскольку
, поскольку  = 0.
= 0.  . По величине нормальное ускорение anАО = ω2* r =
. По величине нормальное ускорение anАО = ω2* r =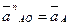 , параллельный АО от А к О. Вектор ускорения точки В находим путем графического решения уравнения
, параллельный АО от А к О. Вектор ускорения точки В находим путем графического решения уравнения  . Вектор
. Вектор  направлен параллельно ВА от В к А, его величина равна anВА = VВА2/ l = 13,82/0,45 = 423 м/с2.
направлен параллельно ВА от В к А, его величина равна anВА = VВА2/ l = 13,82/0,45 = 423 м/с2.

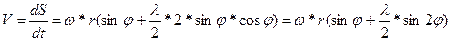 (3.3)
(3.3) (3.4)
(3.4)
 Эвольвентой называется кривая, которую описывает любая точка прямой линии, прокатываемой по окружности без скольжения. Сама окружность называется основной окружностью или эволютой.
Эвольвентой называется кривая, которую описывает любая точка прямой линии, прокатываемой по окружности без скольжения. Сама окружность называется основной окружностью или эволютой. 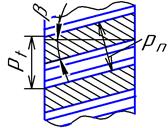 Для косозубых колес вводится понятие окружной шагpt. Из рисунка видим, что pt = pn/cosβ.Величина mt = pt/πназывается окружным модулем. Очевидно соотношение m = mt* cosβили mt = m/ cosβ.
Для косозубых колес вводится понятие окружной шагpt. Из рисунка видим, что pt = pn/cosβ.Величина mt = pt/πназывается окружным модулем. Очевидно соотношение m = mt* cosβили mt = m/ cosβ.