
|
|
Деформация растяжения и сжатияА.К. Китов ПРИКЛАДНАЯ МЕХАНИКА Курс лекций
Предисловие Курс «Прикладная механика» читается для немашиностроительных специальностей. В учебных планах ряда технических специальностей курс называется по-разному: «Прикладная механика», «Техническая механика», «Механика». Количество лекционных часов, выделяемых на курс, так же разное от 17 до 48 часов. В курсе рассматриваются 4 раздела: сопротивление материалов; основы взаимозаменяемости; основы теории механизмов и машин (ТММ); детали машин. Каждый из этих разделов – это отдельная дисциплина, которая, например, у машиностроителей, изучается в течение одного-двух семестров. В данном курсе на все четыре дисциплины отводится максимум 48 часов на дневной форме обучения. Что касается заочной формы обучения, то здесь максимальное количество лекционных часов – 8. Предполагается, что весь основной материал студент должен освоить самостоятельно. Литературы по каждому разделу достаточно много. В основном это многостраничные монографии, зачастую сильно теоретизированные. Не подготовленному человеку очень сложно выделить из обилия материала ту маленькую часть, имеющую именно прикладное значение, то есть позволяющую решать практические инженерные задачи. Во многих отдаленных представительствах, наоборот, у студентов ситуация усугубляется отсутствием необходимой литературы. Именно вышеизложенные обстоятельства подвигли автора к написанию данного курса. Основная цель курса сформулирована так: в сжатой форме, при использовании только основных (базовых) формул и закономерностей, дать возможность будущим инженерам решать конкретные инженерные задачи, то есть уметь «прикладывать» свои знания. Для достижения этой цели каждый раздел курса построен, как методика решения практических задач. В большинстве случаев методика решения разбирается на конкретных примерах, доведенных до численного значения или до чертежа, то есть до конечного результата. Невозможно включить в краткий курс весь необходимый вспомогательный материал: характеристики материалов, таблицы и графики коэффициентов и др. Однако, в раздел «Основы взаимозаменяемости» включены рекомендуемые посадки и ограниченный перечень полей допусков и предельных отклонений; в разделе «Детали машин» приведены необходимые данные для выбора клиновых ремней и роликовых приводных цепей. Очевидно, что для решения более широкого круга задач необходимо привлекать дополнительные источники информации. По каждому разделу дан список литературы. Автор приносит свою благодарность доктору технических наук, профессору Ю.В. Димову, кандидатам технических наук, доцентам Ю.Н. Горнову и П.В. Королеву за все замечания и полезные советы, высказанные по разделам курса. Автор.
I. Основы сопротивления материалов. Что такое сопромат? Сопромат – это наука, которая позволяет инженеру ответить по меньшей мере на три вопроса: 1 – выдержит конструкция приложенную нагрузку или нет?; 2 – что сделать, чтобы выдержала? 3 – на сколько деформируется (растянется, прогнется, закрутится)?.
Очевидно, в первую очередь нужно знать, какие внешние нагрузки действуют на конструкцию.
Внешние силы (нагрузки).
Нагрузки, действующие на конструкцию, представляют собой силы или пары сил (моменты), которые могут рассматриваться как сосредоточенные или распределенные.Распределенные нагрузки могут быть поверхностными (давление ветра или воды на стенку) и объёмными (сила тяжести тела, силы инерции). Сосредоточенные и распределенные нагрузки могут быть как статическими, так и динамическими. Статическими называются нагрузки, которые изменяют свою величину или точку приложения с очень небольшой скоростью, так что возникающими при этом ускорениями, а следовательно и силами инерции можно пренебречь. Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью (ударные нагрузки). При этом возникают силы инерции, которые могут многократно превышать статические нагрузки.
F – сосредоточенная сила (Н); g- распределенная нагрузка (Н/м); Мизг.- момент изгибающий (Н*м);
Рис.1.1 Мкр.- момент крутящий (Н*м) По внешним нагрузкам известно абсолютно всё (величина, точка приложения, угол наклона, направление). Однако, знание внешних нагрузок не дает ответ ни на один вопрос сопромата. Следующим шагом необходимо определить внутренние силы, то есть те реакции конструкции, которые возникают в ответ на внешнее воздействие. Для этих целей служит метод сечений.
1.2. Метод сечений (основной метод определения внутренних усилий). Метод состоит из четырех пунктов. Рассмотрим его на примере стержня, нагруженного несколькими сосредоточенными силами (рис.1.2). При этом считаем, что все силы лежат в одной плоскости и пересекают ось стержня (плоская задача).
1.Мысленно разрежем стержень. 2.Отбросим 1 часть, желательно ту, на которую действует больше сил. 3.В сечении прикладываем внутренние силы, способные уравновесить оставшуюся часть. 4.Находим эти силы из уравнений равновесия П.4
Знак (-) показывает, что участок стержня сжимается. ∑Fy = 0. Q – F2*Sinα= 0. Q = F2*Sinα ∑ М0 = 0. Мизг - F2* h = 0. .Мизг = F2* h Силы N и Q имеют свои названия. N- нормальная сила, поскольку направлена по нормали к сечению. Q- поперечная сила, лежит в плоскости сечения, Рис. 1.2поперек оси стержня. В общем случае в сечении может возникнуть 6 внутренних усилий: N, Qx , Qy , Mx , My, Мкр. Для их нахождения необходимо составить 6 уравнений равновесия. Найденные внутренние усилия еще не дают ответы на поставленные выше вопросы сопромата. Например, у Вас получилось, что нормальная сила N = 100 Н. Тонкая нить под такой силой порвется, а стальной стержень диаметром 10 мм эту силу даже не почувствует. Перейдем к одному из самых основных параметров в сопротивлении материалов – напряжения.
Напряжения
Когда говорят о напряжениях, то имеют в виду напряжение в точке сечения. Учитывая принятое в сопротивлении материалов допущение, что материал детали однороден и изотропен, получаем, что напряжения в каждой точке сечения одинаковы. Следовательно приведенное выше Рис. 1.3 определение напряжения справедливо. Обратимся к рис.1.3. В сечении стержня выделена маленькая площадка ∆A, на которой действует внутренняя сила ∆R. Тогда среднее напряжение на площадке равно Рср = ∆R/∆A. Уменьшая размеры площадки до уровня точки, получим Р = lim ∆R/∆A = dR/dA – напряжение в точке сечения. ∆A→0 Полное напряжение Р можно разложить на две составляющие: 1)составляющую, нормальную к плоскости сечения σ - нормальное напряжение; 2)составляющую, лежащую в плоскости сечения τ - касательное или тангенциальное напряжение. Размерность напряжений. Напряжения измеряются в МПа. 1МПа= 1МПа=1Н/мм² Очевидно, что реальные (расчетные) напряжения в конструкции не могут расти до бесконечности, они должны быть ограничены.
Решение любой прочностной задачи не возможно без знания численных значений допустимых напряжений. Во многих типовых расчетах, например в курсовом проектировании, Вам эти значения будут даны. Однако, в большинстве реальных инженерных расчетов такого не будет и Вам самим придется решать зту проблему. Прежде чем перейти к методике ее решения, рассмотрим вспомогательный материал.
Диаграмма растяжения
образца. а) Рис.1 б) В виде а) информация потребителю не нужна, поэтому диаграмма перестраивается в координатах σ и ε – относительная деформация. На диаграмме выделяются 3 характерных точки σпц – предел пропорциональности, σТ – предел текучести и σв - временное сопротивление или предел прочности. После обработки результатов испытаний в справочную литературу передаются данные, имеющие наименьшую погрешность – это в первую очередь σв, затем σТ , а σпцвы можете встретить крайне редко, только в специальной литературе. А теперь внимательно посмотрите на диаграмму и ответьте на вопрос, какие напряжения Вы можете брать в качестве допустимых? σв– очевидно нет, поскольку Вы заведомо закладываете в конструкцию ее разрушение; σТ - крайне не желательно, при этих напряжениях в конструкции возникнут значительные, необратимые пластические деформации; σпц – можно, только Вам его никто не дал. Получается замкнутый круг, что дано – брать нельзя, а что можно брать – то не дано. Выход из этого круга Вам предлагают искать самим. [σ] = σв/n , (1.1) где n = 1,2 … 10 – коэффициент запаса прочности.
Коэффициент запаса прочности – это Ваш опыт, страх и риск. Могу Вам дать только небольшой совет. Условия работы конструкции: неопасные n = 1,2 … 2,5 ; средней опасности n = 2,5 … 5; повышенной и высокой опасности n = 5 … 10 и более. На данный момент Вы уже многое знаете. Знаете, что такое напряжение, какие виды напряжений бывают, можете определить внутренние силы, можете решить вопрос с допустимыми напряжениями. Вы готовы к решению прочностных задач. Поэтому перейдем к рассмотрению конкретных видов деформаций.
Деформация растяжения и сжатия Этот вид деформации показан на рис.1.5.
Δd = d – d1 – абсолютная поперечная деформация. ε = Δl/l – относительная продольная деформация. ε1 = Δd/d – относительная поперечная деформация. Очевидно, что эти две деформации взаимосвязаны. Первым эту связь установил Пуассон. Рис. 1.5 Запишем коэффициент Пуассона. μ = ε1/ ε = 0,25…0,33 ≈ const. При растяжении или сжатии внутри стержня возникают только нормальные силы, а значит только нормальные напряжения. Поэтому можем записать условие прочности. σ = Ν/Α ≤ [σ] - условие прочности при растяжении (сжатии) (1.2) Между напряжением и относительной продольной деформацией существует зависимость, которую первым установил Гук. Запишем закон Гука. σ = Е*ε (1.3) - напряжение пропорционально относительной продольной деформации. Здесь Е– модуль упругости первого рода или просто модуль упругости.Он характеризует жесткость материала, то есть его способность сопротивляться деформированию. Для стали Е = 2*105 МПа. Закон Гука можно записать и в другом виде. Подставив вместо σ = Ν/Α, а вместо ε = Δl/l, получим Δl = Ν*l/( Е*Α) (1.4) Формула (1.4) позволяет определить абсолютную продольную деформацию, то есть ответить на 3-й вопрос сопромата.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 На рис.1.1 показаны различные нагрузки, действующие на двухопорную балку.
На рис.1.1 показаны различные нагрузки, действующие на двухопорную балку.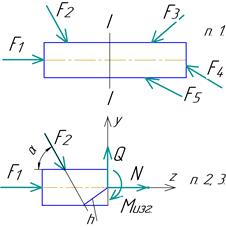 ∑Fz = 0. N+F1+F2*Cosα = 0. N = - (F1+F2*Cosα )
∑Fz = 0. N+F1+F2*Cosα = 0. N = - (F1+F2*Cosα )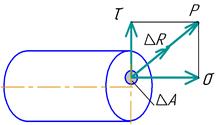 Напряжение пропорционально внутреннему усилию и обратно пропорционально площади поперечного сечения.
Напряжение пропорционально внутреннему усилию и обратно пропорционально площади поперечного сечения. Па=
Па=  Н/мм²
Н/мм²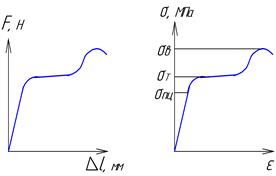 Прежде чем исходные данные по напряжениям поступят в справочную литературу, их надо получить. Получают их, проводя серии испытаний на образцах из данного материала. Первый вид испытаний – это испытание на разрыв. Образец закрепляется в разрывной машине и растягивается до полного разрушения. При этом фиксируются сила и деформация образца. Большинство материалов, с которыми нам приходится сталкиваться (стали, алюминиевые и медные сплавы и др.) относятся к группе упруго-пластичных материалов. Их диаграмма растяжения выглядит, как показано на рис.1.4а. Сначала деформация растет пропорционально силе, затем резкое увеличение деформации (текучесть материала), снова сопротивление и разрыв
Прежде чем исходные данные по напряжениям поступят в справочную литературу, их надо получить. Получают их, проводя серии испытаний на образцах из данного материала. Первый вид испытаний – это испытание на разрыв. Образец закрепляется в разрывной машине и растягивается до полного разрушения. При этом фиксируются сила и деформация образца. Большинство материалов, с которыми нам приходится сталкиваться (стали, алюминиевые и медные сплавы и др.) относятся к группе упруго-пластичных материалов. Их диаграмма растяжения выглядит, как показано на рис.1.4а. Сначала деформация растет пропорционально силе, затем резкое увеличение деформации (текучесть материала), снова сопротивление и разрыв В каждом конкретном случае Вамсамим придется решать, какой коэффициент запаса прочности выбрать. Возьмете маленький коэффициент – конструкция будет легкой, но может разрушиться. Возьмете большой коэффициент – конструкция может оказаться слишком громоздкой и тяжелой. Поиск компромиса – довольно серьезная проблема. Очень многое будет зависеть от условий, в которых будет работать Ваше изделие с точки зрения опасности. Например, Вам нужно спроектировать две однотипных тележки, только одна предназначена для дачи, а на другой будут перевозить бутыли с сверхядовитым веществом и поломка этой тележки чревата катастрофическими последствиями. Одинаковый ли коэффициент запаса прочности Вы возьмете в этих случаях ?
В каждом конкретном случае Вамсамим придется решать, какой коэффициент запаса прочности выбрать. Возьмете маленький коэффициент – конструкция будет легкой, но может разрушиться. Возьмете большой коэффициент – конструкция может оказаться слишком громоздкой и тяжелой. Поиск компромиса – довольно серьезная проблема. Очень многое будет зависеть от условий, в которых будет работать Ваше изделие с точки зрения опасности. Например, Вам нужно спроектировать две однотипных тележки, только одна предназначена для дачи, а на другой будут перевозить бутыли с сверхядовитым веществом и поломка этой тележки чревата катастрофическими последствиями. Одинаковый ли коэффициент запаса прочности Вы возьмете в этих случаях ?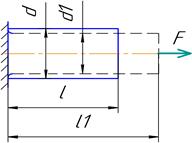 Δl = l1- l – абсолютная продольная деформация.
Δl = l1- l – абсолютная продольная деформация.