ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРИЧЕСКОМ И МАГНИТНОМ ПОЛЯХ

Движение в однородных электрическом и магнитном полях

Мы теперь перейдем к описанию в общих чер­тах движения зарядов в различных условиях. Наиболее интересные явления возникают тогда, когда зарядов движется много и все они взаимо­действуют друг с другом. Так обстоит дело, когда электромагнитные волны проходят через кусок вещества или плазму; тогда легионы за­рядов взаимодействуют друг с другом. Но это очень сложная картина. Позднее мы поговорим и о таких проблемах; пока же мы обсудим не­сравненно более простую задачу о движении отдельного заряда в заданном поле. При этом можно пренебречь всеми другими зарядами, за исключением, разумеется, тех зарядов и токов, которые создают предполагаемое нами поле.

Начать, по-видимому, нужно с движения частицы в однородном электрическом поле. Движение при небольших скоростях не пред­ставляет особенного интереса — это просто рав­номерно ускоренное движение в направлении поля. А вот когда частица, набрав достаточно энергии, превращается в релятивистскую, дви­жение ее становится более сложным. Решение для этого случая я оставляю вам — потруди­тесь и отыщите его сами.

Мы же рассмотрим движение в однородном магнитном поле, когда электрического поля нет. Эту задачу мы уже решали. Одним из ре­шений было движение частиц по окружности. Магнитная сила

qv X В всегда действует под прямым углом к направлению движения, так что производная dp/dt перпендикулярна р и равна по величине vp/R, где R — радиус окружности, т. е.

Фиг. 29.1. Движение частицы в однородном магнитном поле.

Таким образом, радиус круговой орбиты равен

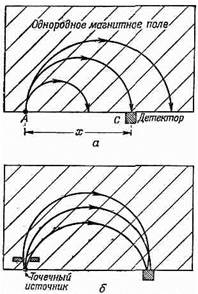
(29.1)

Это одно из возможных движений. Если движущаяся час­тица имеет только одну составляющую в направлении поля, то она не изменяется, ибо у магнитной силы отсутствует компо­нента в направлении поля. Общее же движение частицы в од­нородном магнитном поле — это движение с постоянной ско­ростью в направлении В и круговое движение под прямым углом к В, т. е. движение по цилиндрической спирали (фиг. 29.1). Радиус спирали определяется равенством (29.1) с заменой р на р_┴ — компоненту импульса, перпендикулярную к направ­лению поля.

Анализатор импульсов

Однородное магнитное поле часто применяется в «анализа­торе», или «спектрометре импульсов» высокоэнергетических частиц. Предположим, что в точке А (фиг. 29.2, а) в однородное магнитное поле влетают заряженные частицы, причем магнит­ное поле перпендикулярно плоскости рисунка. При этом каж­дая частица будет лететь по круговой орбите, радиус которой пропорционален ее импульсу. Если все частицы влетают в поле перпендикулярно его краю, то они покидают его на расстоянии х от точки А, пропорциональном их импульсу р. Помещенный в некоторой точке С счетчик будет регистрировать только та­кие частицы, импульс которых находится где-то в интервале Dр величин p=qBx/2.

Фиг. 29.2. 180-градусный спек­трометр импульсов с однородным магнитным полем.

а — траектории частиц с разными импульсами; 6 — траектории частиц, влетающих под равными углами. Маг­нитное поле направлено перпендикулярно плоскости рисунка.

Нет необходимости, разу­меется, чтобы перед регист­рацией частица поворачива­лась на 180°, но такой «180-градусный спектрометр» обладает особым свойством: для него совсем необяза­тельно, чтобы частицы вхо­дили под прямым углом к краю поля. На фиг. 29.2, б показаны траектории трех частиц с одинаковым импульсом, но входящих в поле под различными углами. Вы видите, что траектории у них разные, но все они покидают поле очень близко к точке С. В подобных случаях мы говорим о «фокусировке». Преимущество такого способа фо­кусировки в том, что она позволяет допускать в точку А частицы, летящие под большими углами, хотя обычно, как видно из рисунка, углы эти в какой-то степени ограничены. Большое угловое разрешение обычно означает регистрацию за данный промежуток времени большего числа частиц и сокращения, следовательно, времени измерения.

Изменяя магнитное поле, передвигая счетчик вдоль оси х или же покрывая с помощью многих счетчиков целую область по оси х, можно измерить «спектр» падающего пучка [«спектр» им­пульсов f(p) означает, что число частиц с импульсами в интер­вале между р и (p+dp) равно f(p)dp]. Такие измерения про­водятся, например, при определении распределения по энер­гиям в b-распаде различных ядер.

Имеется еще много других типов импульсных спектрометров, но я расскажу вам только об одном из них, характерном особен­но большим разрешением по пространственному углу. В основе его лежат винтовые орбиты в однородном поле, как это показано на фиг. 29.1. Представьте себе цилиндрическую систему коорди­нат r, q, z, причем ось z выбрана по направлению магнитного поля. Если частица испускается из начала координат под углом

Фиг. 29.3. Спектро­метр с аксиальным полем.

а к направлению оси z, то она будет двигаться по спиральной линии, описываемой выражением

входящие туда параметры а, bи k нетрудно выразить через r, a и магнитное ноле В. Если для данного импульса, но разных начальных углов отложить расстояние r от оси как функцию z, то мы получим кривые, подобные сплошным кривым на фиг. 29.3. (Вы помните — ведь это своего рода проекция винтовой траек­тории.) Когда угол между осью и начальным направлением велик, максимальное значение r тоже будет большим, а продоль­ная скорость при этом уменьшается, так что выходящие под раз­личными углами траектории стремятся собраться в своего рода фокус (точка А на рисунке). Если на расстоянии А поставить узкое кольцевое отверстие, то частицы, летящие в некоторой области углов, могут пройти через отверстие и достигнуть оси, где для их регистрации мы приготовим протяженный детектор D. Частицы, вылетающие из начала координат под тем же са­мым углом, но с большим импульсом, летят по пути, обозначен­ному нами пунктирной линией, и не могут пройти через отвер­стие А. Итак, прибор выбирает небольшой интервал импульса. Преимущество такого спектрометра по сравнению с описанным ранее состоит в том, что отверстия А и А' можно сделать коль­цевыми, так что могут быть зарегистрированы частицы в до­вольно большом телесном угле. Это преимущество особенно важно для слабых источников и при очень точных измерениях, когда необходимо использовать возможно большую долю испу­щенных источником частиц.

Фиг. 29.4. Внутри эллип­соидальной катушки, ток которой на любом интер­вале оси Dx одинаков, воз­никает однородное поле.

Но за это преимущество приходится расплачиваться, ибо метод требует большого объема однородного магнитного поля, и он практически пригоден только для частиц с небольшой энергией. Если вы помните, один из способов получения одно­родного поля — это намотать провод на сферу так, чтобы поверх­ностная плотность тока была пропорциональна синусу угла. Вы можете доказать, что то же самое справедливо и для эллипсо­ида вращения. Поэтому очень часто такой спектрометр изготов­ляют, просто наматывая эллипсоидальные витки на деревянный или алюминиевый каркас. Единственное, что при этом требует­ся,— это чтобы ток на любом интервале оси Ах (фиг. 29.4) был одним и тем же.

Электростатическая линза

Фокусировка частицы имеет множество применений. Напри­мер, в телевизионной трубке электроны, вылетающие из катода, фокусируются на экране в маленькое пятнышко. Делается это для того, чтобы отобрать электроны одинаковой энергии, но летящие под различными углами, и собрать их в небольшую точ­ку. Эта задача напоминает фокусировку света с помощью линз, поэтому устройства, которые выполняют такие функции, тоже называются линзами.

В качестве примера электронной линзы здесь приведена фиг. 29.5. Это «электростатическая» линза, действие которой зависит от электрического поля между двумя соседними электро­дами. Работу ее можно понять, проследив за тем, что она делает с входящим слева параллельным пучком частиц. Попав в об­ласть а, электроны испытывают действие силы с боковой ком­понентой, которая прижимает их к оси. В области bэлектроны, казалось бы, должны получить равный по величине, но проти­воположный по знаку импульс, однако это не так. К тому вре­мени, когда они достигнут области b, энергия их несколько увеличится, и поэтому на прохождение области bони затратят меньше времени.

Фиг. 29.5. Электростатическая линза. Показаны силовые линии, т. е. линии вектора qE.

Силы-то те же самые, но время их действия меньше, поэтому и импульс будет меньше. А полный импульс силы при прохождении областей а и bнаправлен к оси, так что в результате электроны стягиваются к одной общей точке. По­кидая область высокого напряжения, частицы получают доба­вочный толчок по направлению к оси. В области с сила направ­лена от оси, а в области d — к оси, но во второй области час­тица остается дольше, так что снова полный импульс направлен к оси. Для небольших расстояний от оси полный импульс силы на протяжении всей линзы пропорционален расстоянию от оси (понимаете почему?), и это как раз основное условие, необхо­димое для обеспечения фокусировки линз такого типа.

С помощью этих же рассуждений вы можете убедиться, что фокусировка будет достигнута во всех случаях, когда потенциал в середине электрода по отношению к двум другим либо положи­телен, либо отрицателен. Электростатические линзы такого типа обычно используются в катоднолучевых трубках и некоторых электронных микроскопах.

Магнитная линза

: Есть еще один сорт линз — их часто можно встретить в электронных микроскопах — это магнитные линзы. Схемати­чески они изображены на фиг. 29.6. Цилиндрически симметрич­ный электромагнит с очень острыми кольцевыми наконечниками полюсов создает в малой области очень сильное неоднородное магнитное поле. Оно фокусирует электроны, летящие вертикаль­но через эту область. Механизм фокусировки нетрудно понять; посмотрите увеличенное изображение области вблизи наконеч­ников полюсов на фиг. 29.7. Вы видите два электрона а и b, которые покидают источник S под некоторым углом по отноше­нию к оси. Как только электрон а достигнет начала поля, го­ризонтальная компонента поля отклонит его в направлении от вас. Он приобретет боковую скорость и, пролетая через сильное вертикальное поле, получит импульс в направлении к оси. Бо­ковое же движение убирается магнитной силой, когда электрон покидает поле, так что оконча­тельным эффектом будет им­пульс, направленный к оси, плюс «вращение» относительно нее.

Фиг. 29.6. Магнитная линза.

Фиг. 29.7. Движение электрона в магнитной линзе.

На частицу bдействуют те же силы, но в противоположном направлении, поэтому она тоже отклоняется по направлению к оси. На рисунке видно, как расходящиеся электроны соби­раются в параллельный пучок. Действие такого устройства подобно действию линзы на находящийся в ее фокусе объект. Если бы теперь вверху поставить еще одну такую же линзу, то она бы сфокусировала электроны снова в одну точку и по­лучилось бы изображение источника S.

Электронный микроскоп

Вы знаете, что в электронный микроскоп можно «увидеть» предметы, которые недоступно малы для оптического микроско­па. В гл. 30 (вып. 3) мы обсуждали общие ограничения любой оптической системы, вызываемые дифракцией на отверстии линзы. Если отверстие объектива видно из источника под углом 2q (фиг. 29.8), то две соседние точки, расположенные около источника, будут неразличимы, если расстояние между ними

Фиг. 29.8. Разрешение микроскопа ограничивается угловым размером объектива относительно фокуса.

Фиг. 29.9. Сферическая аберрация линзы.

по порядку величины меньше

где l — длина волны света. Для лучших оптических микроско­пов угол 6 приближается к тео­ретическому пределу 90°, так что б приблизительно равно l, или около 5000 Å.

Тe же самые ограничения применимы и к электронному ми­кроскопу, но только длина волн в нем, т, е. длина волны электро­нов с энергией 50 кв, составляет 0,05 Å. Если бы можно было использовать объектив с отверстием около 30°, то мы способны были бы различить объекты величиной в ¹/₅ А. Атомы в молекулах обычно расположены на расстоянии 1—2 Å, следователь­но, тогда вполне можно было бы получать фотографии молекул. Биология стала бы куда проще; мы бы могли сфотографировать структуру ДНК. Как это было бы замечательно! Ведь все сегод­няшние исследования в молекулярной биологии — это попытки определить структуру сложных органических молекул. Если бы мы были способны их видеть!

Но к несчастью, самая лучшая разрешающая способность электронных микроскопов приближается только к 20 Å. А все потому, что до сих пор никому не удалось построить линзу с большой светосилой. Все линзы страдают «сферической абер­рацией». Это означает вот что: лучи, идущие под большим углом к оси, и лучи, идущие близко к ней, фокусируются в раз­ных точках (фиг. 29.9). С помощью специальной технологии из­готовляются линзы для оптических микроскопов с пренебрежимо малой сферической аберрацией, но никому до сих пор не уда­лось получить электронную линзу, лишенную сферической абер­рации. Можно показать, что для любой электростатической или магнитной линзы описанных нами типов сферическая аберра­ция неизбежна. Наряду с дифракцией аберрация ограничивает разрешающую способность электронных микроскопов ее со­временным значением.

Ограничения, о которых мы упоминали, не относятся к электрическим и магнитным полям, не имеющим осевой симмет­рии или не постоянным во времени. Вполне возможно, что в

один прекрасный день кто-нибудь придумает новый тип электрон­ных линз, свободных от аберрации, присущей простым электрон­ным линзам. Тогда можно будет непосредственно фотографиро­вать атомы. Возможно, что когда-нибудь химические соедине­ния будут анализироваться просто визуальным наблюдением за расположением атомов, а не по цвету какого-то осадка!

Не нашли, что искали? Воспользуйтесь поиском по сайту: