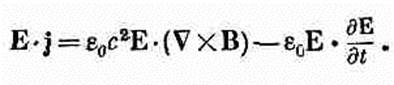Плотность энергии и поток энергии в электромагнитном поле

Идея заключается в том, что должны существовать плот­ность энергии u и поток S, которые зависят только от полей Е и В. [В электростатике, например, плотность энергии, как мы знаем, можно записать в виде ¹/₂e₀(Е•Е).] Разумеется, u и S могут зависеть от потенциалов и чего-то другого, но давайте лучше посмотрим, что мы можем написать. Попытаемся перепи­сать величину Е•j в таком виде, чтобы она стала суммой двух слагаемых, одно из которых было бы производной по времени от некоторой величины, а второе — дивергенцией. Тогда первую величину мы бы назвали и, а вторую — S (разумеется, с надле­жащими знаками). Обе величины должны быть выражены только через поля, т. е. мы хотим записать наше равенство в виде

(27.6)

причем левая часть уравнения должна выражаться только через поля. Как это сделать? Разумеется, нужно воспользоваться уравнениями Максвелла. Из уравнения для ротора В имеем

Подставляя это в (27.6), получаем выражение его только через Е и В:

(27.7)

Работа частично нами уже закончена. Последнее слагаемое есть производная по времени — это (д/дt)(¹/₂e₀Е•Е).

Итак, ¹/₂e₀Е•Е должно быть по крайней мере частью u. Такое же выражение получалось у нас и в электростатике. А теперь единственное, что нам остается сделать,— это превра­тить в дивергенцию чего-то второе слагаемое.

Заметьте, что первое слагаемое в правой части (27.7) пере­писывается в виде

(27.8)

вы знаете из векторной алгебры, что (aXb)•c равно а•(bXc), поэтому первое слагаемое принимает вид

(27.9)

т. е. получилась дивергенция «чего-то», к которой мы так стре­мились. Получилась, но только все это неверно! Я предупреждал вас, что оператор Ñ только «похож» на вектор, а на самом деле он не «настоящий» вектор. Вспомните, что в дифференциальном исчислении существует дополнительное соглашение: когда опе­ратор производной стоит перед произведением, он действует на все стоящее правее него. В уравнении (27.7) оператор Ñ дей­ствует только на В и не затрагивает Е. Но если бы мы записали его в форме уравнения (27.9), то общепринятое соглашение гово­рило бы, что Ñдействует как на В, так и на Е. Так что это не одно и то же. В самом деле, если расписать Ñ•(ВXЕ) по ком­понентам, то можно убедиться, что оно равно E• (ÑXB) плюс какие-то другие слагаемые. Это напоминает взятие производной от произведения в обычном анализе. Например,

Вместо того чтобы выписать все компоненты Ñ• (BXE), мне бы хотелось показать вам один трюк, очень полезный в за­дачах такого рода. Он позволит вам всюду в выражениях, содер­жащих оператор Ñ, пользоваться правилами векторной алгебры, не попадая впросак. Трюк состоит в отбрасывании (по крайней мере на время) правил дифференциального исчисления относи­тельно того, на что действует оператор производной. Вы знаете, что порядок сомножителей важен в двух различных случаях. Во-первых, в дифференциальном исчислении: f(d/dx)g не то же самое, что g(d/dx)f; и, во-вторых, в векторной алгебре: aXb отличается от bXа. Мы можем, если захотим, на минуту отка­заться от правил дифференциального исчисления. Вместо того чтобы говорить, что производная действует на все стоящее правее от нее, мы примем новое правило, избавляющее нас от порядка, в котором записаны сомножители. После этого мы можем крутить ими, как хотим, без всяких помех.

Вот наше новое правило: с помощью индекса мы будем ука­зывать, на что же именно действует дифференциальный опера­тор; при этом порядок сомножителей не имеет никакого значе­ния. Допустим, что оператор д/дх мы обозначили через D. Тогда символ D_f говорит, что берется производная только функции

Но если мы имеем выражение D_ffg, то оно означает

Заметим теперь, что, согласно нашему новому правилу, fD_fg означает то же самое. Одно и то же выражение можно записать любым из следующих способов:

Вы видите, что D_f может стоять даже после всего. (Странно, почему такому удобному обозначению обычно не учат в книгах по математике и физике.)

Вы, пожалуй, удивитесь: а что, если я хочу написать произ­водную от fg? Если мне нужна производная от обоих членов? Это очень легко: вы пишете D_f(fg)+D_g(fg),т.e.g(df/dx)+f(dg/dx), что в старых обозначениях как раз равно d(fg)/dx.

Вы сейчас увидите, как просто теперь получить новое выра­жение для Ñ•(ВXЕ). Начнем с перехода к новому обозначению и напишем

(27.10)

Как только мы сделали это, уже нет больше нужды придержи­ваться строгого порядка. Мы всегда знаем, что Ñ_E действует только на Е, a Ñ_B действует только на В. При этих обстоятель­ствах оператором Ñ можно пользоваться как обычным вектором. (Разумеется, после того как все будет окончено, нам захочется вернуться к «стандартным» обозначениям, которые обычно используются.) Таким образом, теперь мы можем делать различ­ные перестановки сомножителей. Так, средний сомножитель в уравнении (27.10) можно переписать как Е•(Ñ_BXВ). [Надеюсь, вы помните, что a•(bXc) = b•(cXa).] А последний — как В•(EXÑ_E). Хотя это выглядит несколько странно, но тем не менее здесь все в порядке. Если же мы теперь попытаемся вер­нуться к старым обозначениям, то должны будем расположить операторы Ñ так, чтобы они действовали на свои «собственные» переменные. В первом из них все в порядке, так что мы можем просто опустить индекс у Ñ. Второй же требует некоторой реорганизации, чтобы оператор Ñ поставить перед Е. Этого можно
добиться, переставляя сомножители в векторном произ­ведении и меняя знак:

Теперь все стоит на своем месте и можно вернуться к обычным обозначениям. Формула (27.10) эквивалентна следующему равенству:

(В этом специальном случае быстрее было бы использовать ком­поненты, но, право же, стоило потратить время ради того, чтобы показать вам математический трюк. Может случиться, что вы больше нигде его не встретите, а он очень удобен тогда, когда в векторной алгебре нужно освободиться от правила порядка членов при дифференцировании.)

Вернемся теперь к нашему закону сохранения энергии, при­чем для преобразования ÑXB в (27.7) мы используем новый результат — равенство (27.11). Вот что оно дает:

Теперь вы видите, что мы почти у цели. Одно из наших сла­гаемых — настоящая производная no t, ее мы используем при образовании и, а другое (превосходная дивергенция) войдет в S. К несчастью, справа в середине осталось еще одно слагаемое, ко­торое не является ни дивергенцией, ни производной по t. Так что пока еще не все закончено. После некоторых размышле­ний мы опять обращаемся к уравнениям Максвелла и, к счастью, обнаруживаем, что (ÑXE) равно —dB/dt.

Это позволяет превратить дополнительный член в чистую производную чего-то по времени:

Вот теперь у вас получилось то, что нужно. Уравнение для энергии переписывается в виде

А это, если мы определим u и S как

(27.14)

и

(27.15)

в точности напоминает уравнение (27.6). (Перестановкой со­множителей в векторном произведении мы добиваемся правиль­ного знака.)

Итак, наша программа успешно выполнена. Из выражения для плотности энергии мы видим, что она представляет сумму «электрической» и «магнитной» плотностей энергии, которые в точности равны выражениям, полученным нами в статике, когда мы находили выражение для энергии через поля. Кроме того, мы получили выражение для вектора потока энергии электромагнитного поля. Этот новый вектор S=e₀c²EXB по имени своего первооткрывателя называется «вектором Пойнтинга». Он говорит нам о скорости, с которой энергия движется в пространстве. Энергия, протекающая в секунду через малую поверхность da, равна S•nda, где n — вектор, перпендикуляр­ный к поверхности da. (Теперь, когда у нас есть формулы для u и S, можете, если хотите, забыть все выкладки.)

Не нашли, что искали? Воспользуйтесь поиском по сайту: