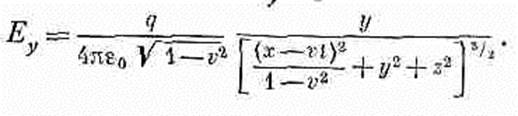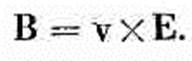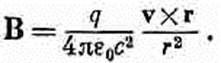Поля точечного заряда, движущегося с постоянной скоростью

Итак, мы нашли потенциалы точечного заряда, движущегося с постоянной скоростью. Для практических целей нам нужно найти поля. Равномерно движущиеся заряды попадаются бук­вально на каждом шагу, скажем проходящие через камеру Вильсона космические лучи или даже медленно движущиеся электроны в проводнике. Так что давайте хотя бы посмотрим, как выглядят эти поля для любых скоростей заряда, даже для скоростей, близких к скорости света, но предположим при этом, что ускорение вообще отсутствует. Это очень интересный вопрос.

Поля мы будем находить по обычным правилам, исходя из потенциалов

Возьмем сначала E_z:

Но компонента A_z равна нулю, а дифференцирование выра­жения (26.1) для j дает

(26.2)

Аналогичная процедура для Е_у приводит к

(26.3)

Немного больше работы с x-компонентой. Производная от j более сложна, да и А_х не равна нулю. Давайте сначала вычислим —дj/дх:

(26.4)

А затем продифференцируем А_х по t:

(26.5)

И, наконец, складывая их, получаем

(26.6)

Бросим на минуту заниматься полем Е, а сначала найдем В. Для его z-компоненты мы имеем

Но, поскольку А_y равна нулю, у нас остается только одна производная. Заметьте, однако, что А_х просто равна vj, а производная (d/dy)vjравна —vE_y . Так что

(26.7)

Аналогично,

или

(26.8)

Наконец, компонента В_х равна нулю, поскольку равны нулю и А_у и А_г. Таким образом, магнитное поле можно запи­сать в виде

(26.9)

Теперь посмотрим, как выглядят наши поля. Мы попытаемся нарисовать картину поля вокруг положения заряда в настоящий момент. Конечно, влияние заряда в каком-то смысле происхо­дит из запаздывающего положения, но, поскольку мы имеем дело со строго заданным движением, запаздывающее положение однозначно определяется положением в настоящий момент. При постоянной скорости заряда поля лучше связывать с теку­щими координатами, ибо компоненты поля в точке х, у, z за­висят только от (х-vt), у и z, которые являются компонентами вектора перемещения r_p из постоянного положения заряда в точку (х, у, z) (фиг. 26.3).

Фиг. 26.3. Электрическое поле заряда, движущегося с постоянной скоростью, направ­лено по радиусу от истинного положения заряда.

Рассмотрим сначала точки, для которых z= 0. Поле Е в этих точках имеет только х- и y-компоненты. Из уравнений (26.3) и (26.6) видно, что отношение этих компонент как раз равно отно­шению х- и y-компонент вектора перемещения. Это означает, что направление Е совпадает с направлением r_p, как это пока­зано на фиг. 26.3. Тот же результат остается справедливым и для трех измерений, поскольку E_z пропорционально z. Короче говоря, электрическое поле заряда радиально и силовые линии расходятся от заряда так же, как и в стационарном случае. Конечно, вследствие наличия дополнительного фактора (1-v²) поле не будет тем же самым, что в стационарном случае. Но здесь мы можем увидеть нечто очень интересное. Дело обстоит так, как будто вы пишете закон Кулона в особой системе коорди­нат, «сжатой» вдоль оси x множителем Ö(1-v²) Если вы сделаете это, то силовые линии впереди и позади заряда разойдутся, а по бокам сгустятся (фиг. 26.4).

Если мы связываем обычным образом напряженность поля Е с плотностью силовых линий, то видим, что поле впереди и по­зади заряда ослабевает, но зато по бокам становится сильнее, т. е. как раз то, о чем говорит нам уравнение. Когда вы изме­ряете напряженность поля под прямыми углами к линии дви­жения, т. е. при (x-vt) = 0, расстояние от заряда будет равно y²+z², а полная напряженность Ö(E²_x+E²_y) в этих точках равна

(26.10)

Она, как и в случае кулонова поля, пропорциональна квад­рату расстояния, но еще усиливается постоянным множителем 1/Ö(1-v²), который всегда больше единицы. Таким образом, по бокам движущегося заряда электрическое поле сильнее, чем это следует из закона Кулона. Фактически увеличение по срав­нению с кулоновым потенциалом равно отношению энергии частицы к ее массе покоя.

Впереди заряда (или позади него) у и z равны нулю, а поэ­тому

(26.11)

Снова поле обратно пропорционально расстоянию от заряда, но теперь оно зарезается множителем (1-v²), что согласуется с картиной силовых линий. Если v/c мало, то v²/c² еще меньше, и действие (1-v²) почти незаметно, поэтому мы снова возвра­щаемся к закону Кулона. Но если частица движется со скоро­стью, близкой к скорости света, то поле перед частицей сильно уменьшается, а поле сбоку чудовищно возрастает.

Наш результат, относящийся к электрическому полю заря­да, можно представить и так. Предположим, что вы на клочке бумаги нарисовали силовые линии покоящегося заряда, а за­тем эту картину запустили со скоростью v₂. Тогда благодаря лоренцеву сокращению рисунок сожмется, т. е. частички гра­фита на бумаге будут казаться нам расположенными в других местах. Но чудо состоит в том, что в результате на про­летающем мимо листочке вы увидите точную картину си­ловых линий точечного дви­жущегося заряда. Лоренцево сокращение сблизит их по бокам, раздвинет перед заря­дом и позади него как раз настолько, чтобы получить нужную плотность. Мы уже отмечали, что силовые ли­нии — это не реальность, а лишь способ представить себе электрическое поле. Однако здесь они ведут себя как самые настоящие реальные линии. В этом частном случае, если вы и сделали ошибку, рассматривая силовые ли­нии как нечто реальное и преобразуя их как реальные линии в пространстве, поле в результате все равно получилось бы пра­вильным.

Фиг.26.4. Электрическое поле заряда.

а — неподвижного, б — летящего с по­стоянной скоростью v=0,9 с.

Однако от этого силовые линии не станут более реаль­ными. Вспомните об электрическом поле, создаваемом зарядом вместе с магнитом; когда магнит движется, он создает новое электрическое поле и разрушает всю нашу прекрасную кар­тину. Так что простая идея сокращающейся картинки, вообще говоря, не годится. Но все же это очень удобный способ запом­нить, как выглядит поле быстро движущегося заряда.

Магнитное поле [из уравнения (26.9)] равно vXE. Когда вы векторно помножите скорость на радиальное поле Е, то полу­чите поле В, силовые линии которого представляют окружности вокруг линии движения (фиг. 26.5). Если же теперь мы подста­вим обратно все с, то вы убедитесь, что результат получился тот же, что и для медленно движущихся зарядов. Хороший способ установить, куда должны войти с, — это вспомнить фор­мулу для силы:

Вы видите, что произведение скорости на магнитное поле имеет ту же размерность, что и электрическое поле, так что в правой части (26.9) должен стоять множитель 1/с², т. е.

(26.12)

Для медленно движущегося заряда (v << с) поле можно считать кулоновым, и тогда

(26.13)

Эта формула в точности соответствует магнитному полю тока, которое было найдено в гл. 14 (вып. 5).

Попутно мне хотелось бы отметить кое-что весьма интерес­ное просто для того, чтобы вы об этом подумали. (К обсуждению этого мы еще вернемся, но несколько позже.) Представьте себе два электрона, скорости которых перпендикулярны, так что пути их пересекаются, однако электроны не сталкиваются; один из них успевает проскочить перед другим. В какой-то момент их относительное положение будет таким, как изображено на фиг. 26.6, а.

Фиг. 26.5. Магнитное поле вблизи движущегося заряда равно vXE (ср. с фиг. 26.4).

Фиг. 26.6. Силы между двумя движущимися заря­дами не всегда равны и противоположны. «Действие», оказывается, не равно «противодействию».

Рассмотрим теперь силы, с которыми q₂ дей­ствует на q₁, и наоборот. На q₂ со стороны q₁ действует только электрическая сила, ибо q₁на линии своего движения не соз­дает магнитного поля. Однако на q₁кроме электрического поля, действует еще и магнитное, так что он движется и в магнитном поле, создаваемом зарядом q₂. Все эти силы показаны на фиг. 26.6, б. Электрические силы, действующие на q₁и q₂, равны по величине и противоположны по направлению. Однако на q₁еще действует и боковая (магнитная) сила, которой и в помине нет у q₂. Равно ли здесь действие противодействию? Поломайте голову над этим вопросом.

Не нашли, что искали? Воспользуйтесь поиском по сайту: