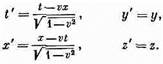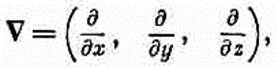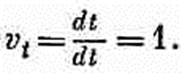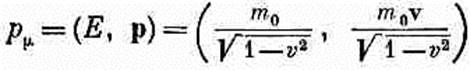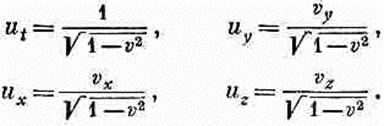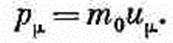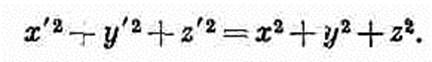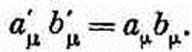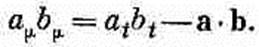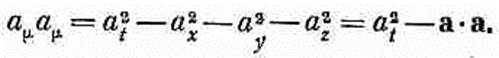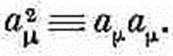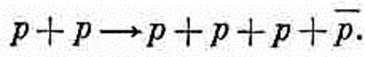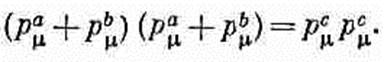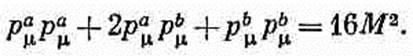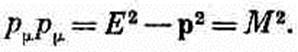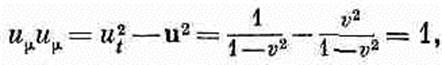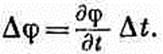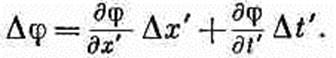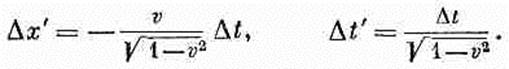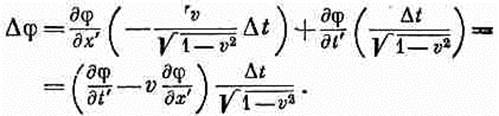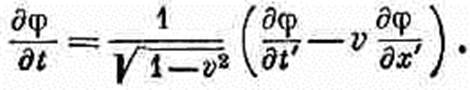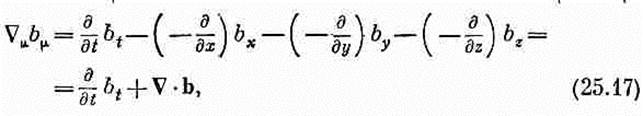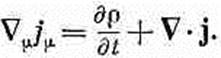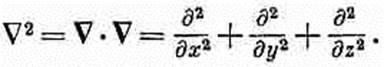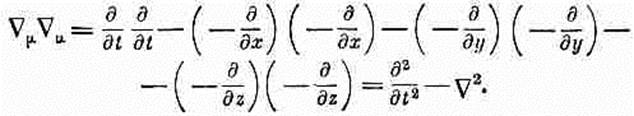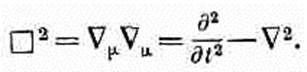В РЕЛЯТИВИСТСКИХ ОБОЗНАЧЕНИЯХ

Четырехвекторы

Скалярное произведение

Четырехмерный градиент

Электродинамика в четырехмерных обозначениях

Четырехмерный потенциал движущегося заряда

§ 6. Инвариантность уравнений электродинамики

В этой главе с=1

Повторить: гл. 15 (вып. 2) «Специ­альная теория от­носительности» ; гл. 16 (вып. 2) «Релятивистская энергия и им­пульс»;

гл. 17 (вып. 2} «Пространство - время»; гл. 13 (вып. 5) «Магнитостатика»

Четырехвекторы

В этой главе мы рассмотрим применение спе­циальной теории относительности к электроди­намике. Мы изучали теорию относительности довольно давно (гл. 15—17, вып. 2), поэтому я здесь коротко напомню основные идеи.

Экспериментально установлено, что законы физики при равномерном движении не изме­няются. Если вы находитесь внутри звездо­лета, летящего с постоянной скоростью по пря­мой линии, то не можете установить самого фак­та движения корабля: для этого надо выглянуть наружу или по крайней мере провести какие-то наблюдения, связанные с внешним миром. Лю­бой написанный нами истинный закон физики должен быть сформулирован так, чтобы этот факт природы был «встроен» в него.

Соотношение между пространством и време­нем в двух системах координат (одна из которых 6" равномерно движется относительно другой 5 в направлении оси х со скоростью v) опреде­ляется преобразованиями Лоренца

(25.1)

Законы физики должны быть таковы, чтобы после преобразований Лоренца они в новой фор­ме выглядели абсолютно так же, как и раньше. Это в точности напоминает принцип независи­мости законов физики от ориентации нашей системы координат. В гл. 11 (вып. 1) мы видели, что способом математического описания этой инвариантности относительно вращения являет­ся запись уравнений в векторном виде.

Там мы обнаружили, что если, скажем, взять два вектора

то комбинация

при повороте системы координат не меняется. Таким образом, если с обеих сторон уравнения мы видим скалярное произведе­ние, подобное А•В, то уравнение будет иметь в точности ту же форму в любой повернутой системе координат. Кроме того, мы открыли оператор (см. гл. 2)

который, будучи применен к скалярной функции, дает три вели­чины, преобразующиеся в точности как вектор. С помощью это­го оператора был определен градиент, а в комбинации с дру­гими векторами — дивергенция и лапласиан. И, наконец, мы обнаружили, что, составляя суммы некоторых попарных произ­ведений компонент двух векторов, можно получить три вели­чины, которые ведут себя подобно новому вектору. Мы назвали это векторным произведением двух векторов. Используя затем векторное произведение с оператором V, мы определили ротор вектора. В дальнейшем нам часто придется ссылаться на то, что было нами сделано в векторном анализе, поэтому все важнейшие векторные операции в трехмерном пространстве, которые использовались в прошлом, мы собрали в табл. 25.1.

Пользуясь ею, можно так записать любое уравнение физики, что обе его части преобразуются при вращениях одинаковым образом. Если одна его часть — вектор, то вектором должна быть и другая часть, и обе они при вращении системы коор­динат изменяются в точности одинаково. Аналогично, если одна часть скаляр, то скаляром должна быть и другая часть, так что ни та, ни другая не изменяется при вращении системы координат и т. д.

В теории относительности пространство и время неразде­лимо связаны друг с другом, поэтому то же самое придется про­делать и для четырех измерений. Мы хотим, чтобы наши уравне­ния оставались неизменными не только при вращениях, но и при переходе в любую инерциальную систему. Это означает, что наши уравнения должны быть инвариантными относительно преобразований Лоренца (25.1). Цель настоящей главы — пока­зать, как этого можно добиться. Но прежде чем начать, примем соглашение, которое значительно облегчит нашу ра­боту (и к тому же поможет избежать путаницы). Заключается оно в таком выборе единиц измерения длины и времени, чтобы скорость света с оказалась равной единице. Вы можете считать, например, что в качестве единицы времени взят интервал, за который свет проходит отрезок в один метр (это составляет около 3•10^-9 сек). Можно даже так и назвать эту единицу вре­мени: «один световой метр». Использование этой единицы еще ярче оттеняет симметрию пространства и времени. Кроме того, из наших релятивистских уравнений исчезнут все с. (Если это почему-либо вас смущает, то вы можете в любом уравнении вос­становить их или заменить каждое t на ct, а еще лучше вставить с повсюду, где это необходимо для правильной размерности уравнения.) Теперь, после такой подготовки, мы можем дви­нуться дальше.

Наша программа состоит в том, чтобы повторить в четырех­мерном пространстве-времени все то, что мы делали с векто­рами в трех измерениях. Дело это нехитрое — мы просто будем действовать аналогично. Единственное затруднение встретится только при обозначениях (символ вектора у нас уже занят трех­мерными векторами), и несколько изменятся знаки в скалярном произведении.

Прежде всего, по аналогии с векторами в трехмерном про­странстве, введем четырехвектор как набор четырех величин a_t, а_х, а_у и а_z, которые при переходе в движущуюся систему коор­динат преобразуются подобно t, x, у и z. Для обозначения четырехвектора используется несколько различных способов. Мы же будем писать просто а_m, понимая под этим группу четырех ве­личин (a_t, a_x, a_y, a_z); другими словами, значок m принимает ка­кое-либо из четырех «значений»: t, x, у и г. Иногда нам будет удобно обозначать три пространственные компоненты в виде трехмерного вектора, т. е. писать a_m=(a_t , а).

Мы уже сталкивались с одним таким четырехвектором, со­стоящим из энергии и импульса частицы (см. гл. 17, вып. 2). В наших новых обозначениях он запишется так:

p_m=(Е, p), (25.2)

т. е. четырехвектор p_mсостоит из энергии Е и трех компонент трехмерного импульса частицы р.

Похоже, что игра действительно оказывается нехитрой: единственное, что мы должны сделать,— это найти для каждого трехмерного вектора недостающую компоненту и получить четырехвектор. Однако все же эта задача потруднее, чем кажется на первый взгляд. Возьмем, например, вектор скорости с компонентами

Что будет его временной компонентой? Инстинкт подсказывает нам, что поскольку четырехвектор подобен t, x, у, z, то времен­ной компонентой как будто должно быть

Но это неверно. Дело в том, что время t в каждом знаменателе не инвариантно при преобразованиях Лоренца. Числитель имеет правильное поведение, a dt в знаменателе портит все дело: оно не одинаково в двух различных системах.

Оказывается, что четыре компоненты «скорости», которые нам нужно выписать, превратятся в компоненты четырехвектора, если мы попросту поделим их на Ö(1-v²). В правильности этого можно убедиться, взяв
четырехвектор импульса

(25.3)

и поделив его на массу покоя, которая в четырехмерном прост­ранстве является скаляром. Мы получим при этом

(25.4)

что по-прежнему должно быть четырехвектором. (Деление на скаляр не изменяет трансформационных свойств.) Так что четырехвектор скорости v_m можно определить так:

(25.5)

Это очень полезная величина; мы можем теперь написать, например,

(25.6)

Таков типичный вид, который должен иметь правильное реляти­вистское уравнение: каждая сторона его должна быть четырехвектором. (В правой части стоит произведение инварианта на четырехвектор, которое по-прежнему есть четырехвектор.)

Скалярное произведение

То, что расстояние от некоторой точки до начала координат не изменяется при повороте, если хотите,— счастливая случай­ность. Математически это означает, что r²=x²+y²+z² является инвариантом. Другими словами, после поворота r'²=r² или

Возникает вопрос: существует ли подобная величина, которая инвариантна при преобразованиях Лоренца? Да, существует. Из (25.1) вы видите, что

Она была бы всем хороша, если бы только не зависела от наше­го выбора оси х. Но этот недостаток легко исправить вычита­нием y/² и z². Тогда преобразование Лоренца плюс вращение оставляют ее неизменной. Таким образом, роль величины, ана­логичной трехмерному r² в четырехмерном пространстве, играет комбинация

Она является инвариантом так называемой «полной группы Лоренца», которая включает как перемещения с постоянной скоростью, так и повороты.

Далее, поскольку эта инвариантность представляет собой алгебраическое свойство, зависящее только от правил преобра­зования (25.1) плюс вращение, то она справедлива для любого четырехвектора. (Все они, по определению, преобразуются оди­наковым образом.) Так что для любого четырехвектора а_m

Эту величину мы будем называть квадратом «длины» четырехвектора а_м. (Будьте внимательны! Иногда берут обратные зна­ки у всех слагаемых и квадратом длины называют число a²_x+a²_y+a²_z -a²_t)

Если теперь у нас есть два вектора а_m и b_m, то их одноименные компоненты преобразуются одинаково, поэтому комбинация

также будет инвариантной (скалярной) величиной. (Фактически мы доказали это уже в гл. 17, вып. 2.) Получилась величина, совершенно аналогичная скалярному произведению векторов. Мы так и будем называть ее скалярным произведением двух четырехвекторов. Логично, казалось бы, и записывать его а_m•b_m, чтобы оно даже выглядело похожим на скалярное произведение. Но обычно, к сожалению, так не делают и пишут его без точки.

И мы тоже будем придерживаться этого порядка и записывать скалярное произведение просто a_mb_m . Итак, по определению,

(25.7)

Помните, что повсюду, где вы видите два одинаковых значка (вместо m мы иногда будем пользоваться v или другими бук­вами), необходимо взять четыре произведения и сложить их, не забывая при этом о знаке минус перед произведениями про­странственных компонент. С учетом такого соглашения инва­риантность скалярного произведения при преобразованиях Ло­ренца можно записать как

Поскольку последние три слагаемых в формуле (25.7) пред­ставляют просто трехмерное скалярное произведение, то часто удобнее принять такую запись:

Очевидно, что введенную выше четырехмерную длину можно записать как а_mа_m:

(25.8)

Но иногда удобно эту величину записать как а²_m:

Продемонстрируем теперь плодотворность четырехмерного скалярного произведения. Антипротоны (р') получают на боль­ших ускорителях из реакции

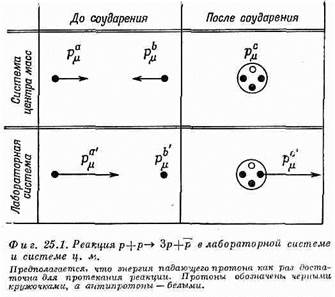
Иначе говоря, высокоэнергетический протон сталкивается с по­коящимся протоном (например, с помещенной в пучок водород­ной мишенью), и если падающий протон обладает достаточной энергией, то вдобавок к двум первоначальным протонам может родиться пара протон—антипротон.

Какой энергией должен обладать падающий протон, чтобы эта реакция стала энергетически возможной?

Ответ легче всего получить, рассмотрев эту реакцию в систе­ме центра масс (ц. м.) (фиг. 25.1). Назовем падающий протон протоном а, а его четырехимпульс обозначим через р^a_m. Анало­гично, протон мишени назовем b, а его четырехимпульс обозна­чим через р^b_m. Если энергии падающего протона как раз достаточ­но для реакции, то в конечном состоянии (т. е. в состоянии после соударения) образуется система, содержащая три протона и ан­типротон, покоящиеся в системе ц. м. Если энергия падающего протона будет несколько выше, то частицы в конечном состоя­нии вылетят с некоторой кинетической энергией и будут разле­таться в стороны; если же она немного ниже, то ее будет недо­статочно для образования четырех частиц.

Пусть р^с_m — полный четырехимпульс всей системы в конеч­ном состоянии, тогда, согласно закону сохранения энергии и

а комбинируя эти два выражения, можно написать

(25.9)

Теперь еще одно важное обстоятельство: поскольку мы по­лучили уравнение для четырехвекторов, то оно должно выпол­няться в любой инерциальной системе. Этим фактом можно вос­пользоваться для упрощения вычислений. Напишем длины каждой из частей (25.9), которые, разумеется, тоже должны быть равны друг другу, т. е.

(25.10)

Так как р^с_m р^с_m — инвариант, то можно вычислить его в ка­кой-то одной системе координат. В системе ц. м. временная компонента р^с_m равна энергии покоя четырех протонов, т. е. 4М, а пространственная часть р равна нулю, так что р^с_m=(4М, 0). При этом мы воспользовались равенством масс протона и антипротона, обозначив их одной буквой М.

Таким образом, уравнение (25.10) принимает вид

(25.11)

Произведения р^а_mр^а_m и p^b_mp^b_m, вычисляются очень быстро: «дли­на» четырехвектора импульса любой частицы равна просто квадрату ее массы:

Это можно доказать прямыми вычислениями или, несколько бо­лее эффектно, простым замечанием, что в системе покоя ча­стицы р_m=(М, 0), а следовательно, р_mр_m=М². А так как это инвариант, то он равен М² в любой системе отсчета. Подставляя результаты в уравнение (25.11), мы получаем

или

(25.12)

Теперь можно вычислить р^а_mр^b_mв лабораторной системе. В этой системе четырехвектор р^а_м = (Е^а, р^а), а р^b_m=(М, 0), ибо он описывает покоящийся протон. Итак, р^а_mр^b_mдолжно быть рав­но МЕ^а, а мы знаем, что скалярное произведение — это инвари­ант, поэтому оно должно быть равно значению, найденному нами в (25.12). В результате получается

Полная энергия падающего протона должна быть по мень­шей мере равна 1М (что составляет около 6,6 Гэв, так как М=938 Мэв) или после вычитания массы покоя М получаем, что кинетическая энергия должна быть равна по меньшей мере 6М (около 5,6 Гэв). Именно с тем, чтобы иметь возможность производить антипротоны, бетатрон в Беркли проектировался на кинетическую энергию ускоренных протонов около 6.2 Гэв.

Скалярное произведение — инвариант, поэтому полезно знать его величину. Что, например, можно сказать о «длине» четырехвектора скорости u_mu_m?

т. е. u_m — единичный четырехвектор.

Четырехмерный градиент

Следующей величиной, которую нам следует обсудить, яв­ляется четырехмерный аналог градиента. Напомним (см. гл. 14, вып. 1), что три оператора дифференцирования д/дх, д/ду, d/dz преобразуются подобно трехмерному вектору и назы­ваются градиентом. Та же схема должна работать и в четырех измерениях; по простоте вы можете подумать, что четырехмер­ным градиентом должны быть (d/dt, д/дх, д/ду d/dz), но это неверно.

Чтобы обнаружить ошибку, рассмотрим скалярную функ­цию, которая зависит только от х и t. Приращение j при малом изменении t на Dt и постоянном х равно

(25.13)

С другой стороны, с точки зрения движущегося наблюда­теля

Используя уравнение (25.1), мы можем выразить Dх' и Dt' через Dt. Вспоминая теперь, что величина х постоянна, так

что Dx=0, мы пишем

Таким образом,

Сравнивая этот результат с (25.13), мы узнаем, что

(25.14)

Аналогичные вычисления дают

(25.15)

Теперь вы видите, что градиент получился довольно странным. Выражения для х и t через х' и t' [полученные решением уравнений (25.1)] имеют вид

Именно так должен преобразовываться четырехвектор. Но в уравнениях (25.14) и (25.15) знаки получились неправильными! Выход в том, что надо заменить неправильное определение четырехмерного оператора градиента (d/dt,Ñ) правильным:

Мы его обозначим Ñ_m . Для такого Ñ_m трудности исчезают, и он ведет себя так, как подобает настоящему четырехвектору. (Ужасно неприятно наличие минусов, но так уж устроено в мире.) Разумеется, говоря, что Ñ_m «ведет себя как четырехвектор», мы подразумеваем, что четырехмерный градиент ска­лярной функции есть четырехвектор. Если j — настоящее ска­лярное (лоренц-инвариантное) поле, то Ñ_mj будет четырехвекторным полем.

Итак, все уладилось. Теперь у нас есть векторы, градиенты и скалярное произведение. Следующий на очереди — инвари­ант, аналогичный дивергенции в трехмерном векторном ана­лизе. Ясно, что аналогом его должно быть выражение Ñ_mb_m, где b_m — векторное поле, компоненты которого являются функ­циями пространства и времени. Мы определим дивергенцию четырехвектора b_m=(b_t , b) как скалярное произведение Ñ_m на b_m:

где Ñ•b — обычная трехмерная дивергенция вектора b. Не забы­вайте внимательно следить за знаками. Один знак минус свя­зан с определением скалярного произведения [формула (25.7)1, а другой возникает от пространственных компонент Ñ_m [форму­ла (25.16)]. Дивергенция, определяемая формулой (25.7), есть инвариант, и для всех систем координат, отличающихся друг от друга преобразованием Лоренца, применение ее приводит к одинаковой величине.

Остановимся теперь на физическом примере, в котором появ­ляется четырехмерная дивергенция. Ею можно воспользоваться при решении задачи о полях вокруг движущегося проводника. Мы уже видели (гл. 13, § 7, вып. 5), что плотность электрического заряда r и плотность тока j образуют четырехвектор j_m=(p, j). Если незаряженный провод переносит ток j_x, то в системе от­счета, движущейся относительно него со скоростью v (вдоль оси х), в проводнике наряду с током появится и заряд [который возникает согласно закону
преобразований Лоренца (25.1)1:

Но это как раз то, что мы нашли в гл. 13. Теперь нужно под­ставить эти источники в уравнение Максвелла в движущейся системе и найти поля.

Закон сохранения заряда в четырехмерных обозначениях тоже принимает очень простой вид. Рассмотрим четырехмерную дивергенцию вектора j_m :

(25.18)

Закон сохранения заряда утверждает, что утекание тока из еди­ницы объема должно быть равно отрицательной скорости уве­личения плотности заряда. Иными словами,

Подставляя это в (25.18), получаем очень простую форму за­кона сохранения заряда:

(25.19)

Благодаря тому, что Ñ_mj_m — инвариант, равенство его нулю в одной системе отсчета означает равенство нулю и во всех дру­гих. Таким образом, если заряд сохраняется в одной системе, он будет сохраняться и во всех других системах координат, дви­жущихся относительно нее с постоянной скоростью.

В качестве последнего примера рассмотрим скалярное про­изведение оператора градиента Ñ_m на себя. В трехмерном про­странстве такое произведение дает лапласиан

Что получится для четырех измерений? Вычислить это очень просто. Следуя нашему правилу скалярного произведения, на­ходим

Этот оператор, представляющий аналог трехмерного лапласиа­на, называется даламбертианом и обозначается специальным

символом

(25.20)

По построению он является скалярным оператором, т. е., если подействовать им, скажем, на четырехвекторное поле, возникает новое четырехвекторное поле. [Иногда даламбертиан определяется с противоположным по отношению к (25.20) зна­ком, так что при чтении литературы будьте внимательны!]

Итак, для большинства величин, перечисленных нами в табл. 25.1, мы нашли их четырехмерные эквиваленты. (У нас еще нет эквивалента векторного произведения, но его нахождение мы оставим до следующей главы.) А теперь соберем в одно место все важнейшие результаты и определения и составим еще одну таблицу (табл. 25.2); она поможет вам лучше запомнить, что во что переходит.

Не нашли, что искали? Воспользуйтесь поиском по сайту: