
|
|
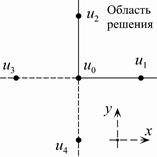
Конечно-разностная аппроксимация для граничных узловРассматриваемый метод позволяет решать задачи для неоднородных сред и со сложной геометрией области. В частности, узлы сетки могут располагаться на границе раздела сред, на краях, в различных углах и т.д. (например, рис. 4.4). Конечно-разностные уравнения для таких узлов отличаются от внутренних. Узлы на границе раздела сред встречаются при исследовании полосковых и микрополосковых линий передачи, частично заполненных волноводов и т.д. На рис. 4.4а показана граница раздела двух сред с параметрами
Поток (4.25) вычисляется по четырём участкам. Потоки
Аналогично потоки
Рис. 4.4. Конечно-разностная аппроксимация для граничных узлов.
Соответственно полный поток (4.25) равен
Перепишем (4.28) в форме основного разностного уравнения
Уравнение (4.39) является основным уравнением центрально-разностной аппроксимации при наличии узлов, расположенных на границе раздела сред. При Задания Задание 4.4 Вычислить методом конечных разностей и нарисовать распределение скалярного потенциала электростатического поля u между двумя бесконечными плоскостями при заданных значениях
a. б. в. г. д. е. ж.
Решение (стр.204, пример 4.9) Краевая задача формулируется как одномерная задача Дирихле (4.9), которая дискретизируется в форме ячеек, содержащих конечное число узлов (три в данном случае), так, что уравнение (4.22) может быть записано для любого узла
которое удобно записать в виде системы относительно
представимая в следующей матричной форме
Используя MATLAB, решаем (4), что с учётом граничных условий даёт Далее по формуле (4.2) теорииможно найти и вектор напряжённости электростатического поля.
clear; clf;
sz=3; h=1/(sz+1); x=0:h:1;
% Полученные матрицы для решения системы уравнений a = [1, -0.5, 0; 0.5, -1, 0.5; 0, -0.5, 1]; b = [0, 0, 1.5]';
v = a \ b;
% По краям матрицы добавляем данные из граничных условий v_final = [0, v', 3];
plot(x,v_final,'o-'); grid; xlabel('x'); ylabel('V');
Задание 4.5 Найти методом конечных разностей и нарисовать распределение скалярного потенциала электростатического поля между двумя поверхностями, если
a. б. в. г. д. е. ж. з. и. к. л. м.
Решение (стр.205, пример 4.10) Краевая задача формулируется как одномерная неоднородная задача Дирихле (4.9), которая дискретизируется в форме ячеек, содержащих конечное число узлов (три в данном случае). Уравнение (4.23) может быть записано для любого узла
Используя (1), ориентируясь на рис. 4.3, выбрав шаг дискретизации
которое удобно записать в виде системы относительно
представимая в следующей матричной форме
Используя MATLAB, решаем (4), что с учётом граничных условий даёт clear; clf;
h=0.25; x=0:h:1;
% Полученные матрицы для решения системы уравнений a = [1, -0.5, 0; -0.5, 1, -0.5; 0, -0.5, 1]; b = [-0.125, -0.125, 1.375]';
v = a \ b;
% По краям матрицы добавляем данные из граничных условий v_final = [0, v', 3];
plot(x,v_final,'o-'); grid; xlabel('x'); ylabel('V');
Задание 4.6 Найти методом конечных разностей вычислить и нарисовать распределение скалярного потенциала электростатического поля u между двумя бесконечными плоскостями при заданных значениях Вычислить методом конечных разностей и нарисовать распределение скалярного потенциала электростатического поля u в бесконечной металлической трубе (двумерная задача), изолированной на углах рис. 4.5. На поверхностях S1 и S2 заданы uS1 = 0 и uS2 = V0. Внутри трубы вводится прямоугольная сетка с шагом Использовать MATLAB для решения системы уравнений. а. uS1 = 0 В, uS2 = V0 = 1 В б. uS1 = 0 В, uS2 = V0 = 2 В в. uS1 = 0 В, uS2 = V0 = 3 В г. uS1 = 0 В, uS2 = V0 = 4 В д. uS1 = 0 В, uS2 = V0 = 5 В е. uS1 = 0 В, uS2 = V0 = 6 В ж. uS1 = 0 В, uS2 = V0 = 7 В
Рис. Геометрия задачи.
Решение Внутри трубы вводится прямоугольная сетка с шагом
которую можно представить в следующей матричной форме
Решив (3) найдём соответствующие значения потенциалов
clear;
a = [4, -1, -1, 0, 0, 0; -2, 4, 0, -1, 0, 0; -1, 0, 4, -1, -1, 0; 0, -1, -2, 4, 0, -1; 0, 0, -1, 0, 4, -1; 0, 0, 0, -1, -2, 4];
v = [1, 1, 0, 0, 0, 0]';
u = a \ v
Результат: u = 0.4286 0.5268 0.1875 0.2500 0.0714 0.0982
Литература К разделу 1 1. Ануфриев И.Е., Смирнов А.Б., Смирнова Е.Н. MATLAB 7. Наиболее полное руководство в подлиннике. БХВ-Петербург, 2005, 1104 с. 2. Дьяконов В. П. MATLAB и SIMULINK для радиоинженеров. — М.: «ДМК-Пресс», 2011, 976 с.
К разделу 2 Основная: 3. Никольский В.В., Никольская Т.И. Электродинамика и распространение радиоволн: Учебн. пособие для вузов.–М.: Наука , 1989. –544 с. 4. Пименов Ю.В., Вольман В.И., Муравцев А.Д. Техническая электродинамика: Учебн. пособие для вузов.–М.: Радио и связь, 2000.–536 с. 5. Баскаков С.И. Электродинамика и распространение радиоволн: Учебн. пособие для вузов.–М.: Высшая школа, 1992.–416 с. 6. Гринев А.Ю., Гиголо А.И. Численное моделирование распространения электромагнитных волн в однородных средах. Учебн. Пособие.–Изд. МАИ, 2012, 42 с. 7. Гринев А.Ю. Численные методы решения прикладных задач электродинамики. М.: Изд. Радиотехника, 2012, 336 с. Дополнительная: 8. Петров Б.М. Электродинамика и распространение радиоволн: Учебник для для вузов.– М.: Горячая линия-Телеком, 2007.–558 с. 9. Неганов В.А., Осипов О.В., Раевский С.Б., Яровой Г.П. Электродинамика и распространение радиоволн: Учебн. пособие для вузов.–М.: Радио и связь, 2005.–648 с.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
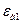 и
и  . Получим конечно-разностное уравнение для центрального узла с потенциалом
. Получим конечно-разностное уравнение для центрального узла с потенциалом  . Полагая, что на границе отсутствуют электрические заряды, воспользуемся уравнением (2.2г) в Теме II, применив его к пунктирной ячейке (задача двумерная) на рис. 4.4а, ограниченной контуром C
. Полагая, что на границе отсутствуют электрические заряды, воспользуемся уравнением (2.2г) в Теме II, применив его к пунктирной ячейке (задача двумерная) на рис. 4.4а, ограниченной контуром C , (4.24)
, (4.24) – нормаль к контуру C;при этом мы воспользовались формулой (4.2):
– нормаль к контуру C;при этом мы воспользовались формулой (4.2):  . Формулу (4.24) можно переписать в виде
. Формулу (4.24) можно переписать в виде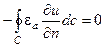 . (4.25)
. (4.25)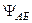 и
и  соответственно равны
соответственно равны . (4.26)
. (4.26) и
и 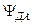 соответственно равны
соответственно равны . (4.27)
. (4.27)


 . (4.28)
. (4.28) . (4.29)
. (4.29) уравнение (4.29) переходит для уравнения Лапласа в (4.22). Заметим, что запись (4.39) очевидным образом следует из (4.22), если брать среднее значение диэлектрических проницаемостей сред
уравнение (4.29) переходит для уравнения Лапласа в (4.22). Заметим, что запись (4.39) очевидным образом следует из (4.22), если брать среднее значение диэлектрических проницаемостей сред  для узлов
для узлов  , расположенных на границе раздела.
, расположенных на границе раздела. на них. Электрические заряды в пространстве между указанными поверхностями отсутствуют. Сравнить с аналитическим решением.
на них. Электрические заряды в пространстве между указанными поверхностями отсутствуют. Сравнить с аналитическим решением.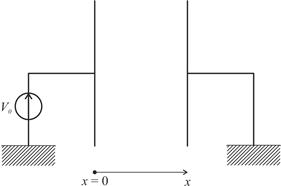
 =0 В,
=0 В,  =3 В, шаг дискретизации по оси x = 0.25 м;
=3 В, шаг дискретизации по оси x = 0.25 м; =0 В,
=0 В,  =3, шаг дискретизации по оси x = 0.2 м;
=3, шаг дискретизации по оси x = 0.2 м; =2 В, шаг дискретизации по оси x = 0.5 м;
=2 В, шаг дискретизации по оси x = 0.5 м; =4 В, шаг дискретизации по оси x = 0.25 м;
=4 В, шаг дискретизации по оси x = 0.25 м;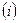 анализируемой области как
анализируемой области как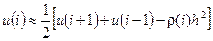 . (1)
. (1) Поскольку
Поскольку  , то, используя (1), ориентируясь на рис. 4.3 и выбрав шаг дискретизации
, то, используя (1), ориентируясь на рис. 4.3 и выбрав шаг дискретизации  для узлов
для узлов  , последовательно имеем представление
, последовательно имеем представление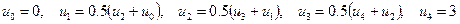 , (2)
, (2)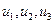
 (3)
(3) . (4)
. (4) , и строим распределение скалярного потенциала электростатического поля между поверхностями. Заметим, что матрица в (4) является разряженной с доминантной главной диагональю.
, и строим распределение скалярного потенциала электростатического поля между поверхностями. Заметим, что матрица в (4) является разряженной с доминантной главной диагональю.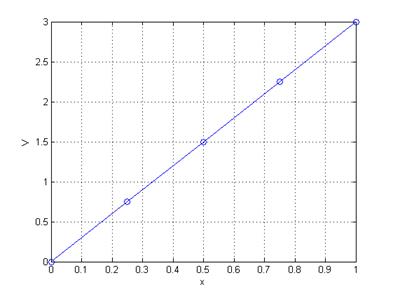
 . Электрические заряды в пространстве
. Электрические заряды в пространстве 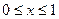 между указанными поверхностями распределены равномерно с плотностью
между указанными поверхностями распределены равномерно с плотностью  . Сравнить с аналитическим решением.
. Сравнить с аналитическим решением.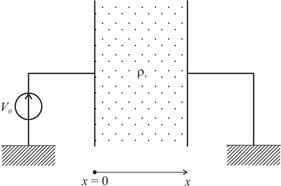
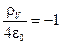 ;
;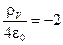 ;
;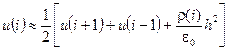 . (1)
. (1) последовательно имеем представление
последовательно имеем представление (2)
(2) (3)
(3) . (4)
. (4) , и строим распределение скалярного потенциала электростатического поля между поверхностями. Заметим, что матрица в (4) является разряженной с доминантной главной диагональю. Далее по формуле (4.2) можно найти и вектор
, и строим распределение скалярного потенциала электростатического поля между поверхностями. Заметим, что матрица в (4) является разряженной с доминантной главной диагональю. Далее по формуле (4.2) можно найти и вектор  напряжённости электростатического поля.
напряжённости электростатического поля.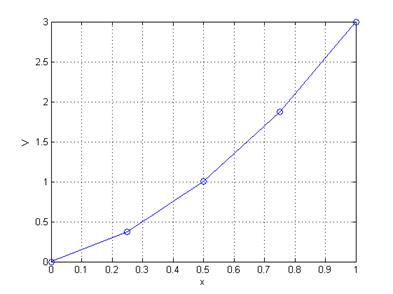
 : 14 фиксированных узлов на поверхности и 9 свободных узлов внутри.
: 14 фиксированных узлов на поверхности и 9 свободных узлов внутри.
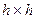 : 14 фиксированных узлов на поверхности (потенциал их задан) и 9 свободных узлов внутри. Поскольку
: 14 фиксированных узлов на поверхности (потенциал их задан) и 9 свободных узлов внутри. Поскольку  внутри трубы, то распределение потенциала находится из решения двумерной однородной задача Дирихле (4.9), и последующим использованием формулы (4.2) для нахождения электростатического поля. Используем разностную форму (4.23) для узлов и значений потенциала на границе в соответствии с рис. 4.3, 4.5 и учтём, что из-за симметрии области относительно оси y
внутри трубы, то распределение потенциала находится из решения двумерной однородной задача Дирихле (4.9), и последующим использованием формулы (4.2) для нахождения электростатического поля. Используем разностную форму (4.23) для узлов и значений потенциала на границе в соответствии с рис. 4.3, 4.5 и учтём, что из-за симметрии области относительно оси y  и
и  . В результате получаем систему
. В результате получаем систему (1)
(1) . (2)
. (2) , а по формуле (4.2) и вектор напряжённости электростатического поля. Заметим, что матрица в (2) является разряженной с доминантной главной диагональю.
, а по формуле (4.2) и вектор напряжённости электростатического поля. Заметим, что матрица в (2) является разряженной с доминантной главной диагональю.