Построение трехмерных графиков

Предыдущая 1 2 3 4 567 8 9 10 11 12 13 14 Следующая

В предыдущих разделах строились графики функции одной переменной (y = f(x)), этот раздел построению трехмерных графиков функции двух переменных (z = f(x, y)). Одним из способов представления таких функций является построение трехмерной поверхности в декартовой системе координат XYZ. При этом параметры функции (x, y) откладываются вдоль соответствующих осей, а значение функции в соответствующих точках откладывается по оси Z.

Для того, чтобы построить график функции двух переменных, предварительно нужно создать сетку, которая задает, в каких точках на плоскости XOY будут рассчитываться значения функции, для этого можно воспользоваться функцией meshgrid со следующим синтаксисом:

[X,Y] = meshgrid(xgv, ygv)

Здесь в качестве входных параметров xgv и ygv задаются одномерные матрицы, определяющие интервалы и шаги сетки вдоль осей X и Y соответственно. Допустим, нужно создать двумерную сетку со следующими параметрами:

· интервал изменения параметра по оси X: [-5; 5] с шагом 1;

· интервал изменения параметра по оси Y: [-12; 12] с шагом 3.

В этом случае создание сетки будет выглядеть следующим образом:

>> meshx = -5: 1: 5;

>> meshy = -12: 3: 12;

>> [X, Y] = meshgrid (meshx, meshy)

X =

-5 -4 -3 -2 -1 0 1 2 3 4 5

Y =

-12 -12 -12 -12 -12 -12 -12 -12 -12 -12 -12

-9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9

-6 -6 -6 -6 -6 -6 -6 -6 -6 -6 -6

-3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3

0 0 0 0 0 0 0 0 0 0 0

3 3 3 3 3 3 3 3 3 3 3

6 6 6 6 6 6 6 6 6 6 6

9 9 9 9 9 9 9 9 9 9 9

12 12 12 12 12 12 12 12 12 12 12

Теперь матрицы X и Y описывают точки, в которых нужно рассчитать значение функции от двух переменных (с использованием поэлементных операций над матрицами). Например, если нужно построить график функции z = x² + y², то нужно выполнить команду:

>> Z = X .^ 2 + Y .^ 2

Z =

169 160 153 148 145 144 145 148 153 160 169

106 97 90 85 82 81 82 85 90 97 106

61 52 45 40 37 36 37 40 45 52 61

34 25 18 13 10 9 10 13 18 25 34

25 16 9 4 1 0 1 4 9 16 25

34 25 18 13 10 9 10 13 18 25 34

61 52 45 40 37 36 37 40 45 52 61

106 97 90 85 82 81 82 85 90 97 106

169 160 153 148 145 144 145 148 153 160 169

Теперь можно построить трехмерный график в виде поверхности. Для этого используется функция surf.

>> surf (X, Y, Z)

В результате будет открыто окно с трехмерной поверхностью (Рис. 2.16).

Рис. 2.16.

Следующий пример демонстрирует построение более сложной функции на интервале [-500; 500] по осям X и Y.

>> meshx = -500: 10: 500;

>> meshy = -500: 10: 500;

>> [X, Y] = meshgrid (meshx, meshy);

>> Z = X .* sin ( sqrt ( abs (X) ) ) + Y .* sin ( sqrt ( abs (Y) ) );

>> surf (X, Y, Z)

В результате будет построен трехмерный график, показанный на рисунке 2.17.

Рис. 2.17.

Подобным образом работает и функция mesh. С той лишь разницей, что при отображении поверхности с помощью функции surf, цветом раскрашивается поверхность (промежутки между линиями сетки), а сетка отображается черными линиями (по умолчанию), а функция mesh строит подобный график, но цветом раскрашивается сетка без закраски самой поверхности. Если изменить предыдущий пример с использованием функции mesh, то будет выведен результат, показанный на рисунке 2.18:

>> meshx = -500: 10: 500;

>> meshy = -500: 10: 500;

>> [X, Y] = meshgrid (meshx, meshy);

>> Z = X .* sin ( sqrt ( abs (X) ) ) + Y .* sin ( sqrt ( abs (Y) ) );

>> mesh (X, Y, Z)

Рис. 2.18.

Для оформления трехмерных графиков также можно использовать функции:

· xlim, ylim, zlim для изменения интервалов, отображаемых по осям;

· xlabel, ylabel, zlabel для добавления подписей к осям;

· title для добавления заголовка к графику;

· text для добавления текстовых надписей

и другие.

Следующий пример демонстрирует использования некоторых из упомянутых выше функций для оформления внешнего вида трехмерных графиков. Результат показан на рисунке 2.19.

>> meshx = -500: 10: 500;

>> meshy = -500: 10: 500;

>> [X, Y] = meshgrid (meshx, meshy);

>> Z = X .* sin ( sqrt ( abs (X) ) ) + Y .* sin ( sqrt ( abs (Y) ) );

>> surf (X, Y, Z)

>> xlabel ('X');

>> ylabel ('Y');

>> zlabel ('Z = f (X, Y)');

>> title ('График функции Швефеля')

>> text (420, 420, 900, 'Max')

Рис. 2.19.

С помощью команды axis off можно отключить отображение осей. Рисунок 2.20 показывает результат вызова этой команды применительно к предыдущему примеру. Для того чтобы показать оси, используется команда axis on.

Рис. 2.20.

Для того чтобы отобразить шкалу цветов, которая показывает, какому значению функции соответствует каждый цвет, предназначена команда colorbar. В результате вызова этой команды после выполнения предыдущего примера окно с графиком примет вид, показанный на рисунке 2.21.

Рис. 2.21.

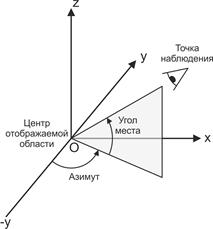
После нажатия кнопки "Rotate 3D" на панели инструментов ( ) или после выбора пункта меню "Tools - Rotate 3D" с помощью мышки можно вращать нарисованный график. Также график можно вращать программно с помощью функции view. Один из вариантов использования функции view заключается в том, что ей передают параметры, описывающие координаты положения "наблюдателя". Координаты могут быть заданы в виде пары азимут – угол места (Рис. 2.22) или в декартовой системе координат.

Рис. 2.22.

Если задавать положение наблюдателя с помощью азимута и угла места, то в функцию view эти углы передаются в виде двух параметров (первый параметр – азимут, второй – угол места). По умолчанию при создании трехмерного графика азимут "наблюдателя" равен -37.5°, а угол места – 30°. Следующий пример строит трехмерную поверхность и изменяет положение точки наблюдения с помощью функции view. Результат показан на рисунке 2.23.

>> meshx = -500: 10: 500;

>> meshy = -500: 10: 500;

>> [X, Y] = meshgrid (meshx, meshy);

>> Z = X .* sin ( sqrt ( abs (X) ) ) + Y .* sin ( sqrt ( abs (Y) ) );

>> surf (X, Y, Z)

>> view (45, 60)

Рис. 2.23.

В качестве альтернативы, вызов функции view может выглядеть следующим образом:

view ([45, 60])

Вызов функции view без входных параметров, но с двумя выходными параметрами возвращает текущее положение "наблюдателя" в системе координатам азимут – угол места:

>> [azimuth, elevation] = view

azimuth =

elevation =

Координаты наблюдателя можно задавать в декартовой системе координат, в этом случае координаты по осям X, Y, Z нужно объединять в матрицу из трех:

>> meshx = -500: 10: 500;

>> meshy = -500: 10: 500;

>> [X, Y] = meshgrid (meshx, meshy);

>> Z = X .* sin ( sqrt ( abs (X) ) ) + Y .* sin ( sqrt ( abs (Y) ) );

>> surf (X, Y, Z)

>> xlabel ('X')

>> ylabel ('Y')

>> view ([-200 500 600])

Результат показан на рисунке 2.24.

Рис. 2.24.

Чтобы вернуть положение "наблюдателя" к значению по умолчанию (азимут равен -37.5°, а угол места – 30°), нужно вызвать функцию view в виде:

>> view (3)

Если функцию view вызвать в виде view(2), то график будет повернут таким образом, чтобы смотреть на него строго вертикально (азимут будет равен 0°, а угол места будет равен 90°). Это продемонстрировано в следующем примере и на рисунке 2.25.

>> meshx = -500: 10: 500;

>> meshy = -500: 10: 500;

>> [X, Y] = meshgrid (meshx, meshy);

>> Z = X .* sin ( sqrt ( abs (X) ) ) + Y .* sin ( sqrt ( abs (Y) ) );

>> surf (X, Y, Z)

>> xlabel ('X')

>> ylabel ('Y')

>> view(2)

Рис. 2.25.

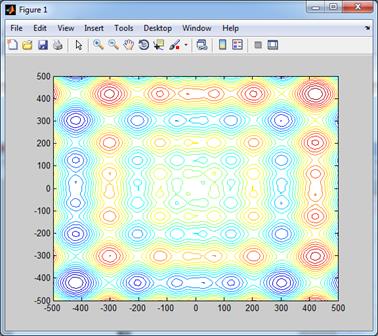
Построение линий уровня

Построение линий уровня очень похоже на построение трехмерных графиков. Для этого сначала также необходимо создать двумерную сетку, в узлах которой будут рассчитываться значения функций, а затем для построения линий уровня используется функция contour, параметры которой во многом напоминают параметры функций surf и mesh, описанных в предыдущем разделе. Следующий пример строит линии уровня функции Швефеля, результат показан на рисунке 2.26.

>> meshx = -500: 10: 500;

>> meshy = -500: 10: 500;

>> [X, Y] = meshgrid (meshx, meshy);

>> Z = X .* sin ( sqrt ( abs (X) ) ) + Y .* sin ( sqrt ( abs (Y) ) );

>> contour (X, Y, Z)

Рис. 2.26.

Функцию contour можно использовать с дополнительным параметром: contour (X, Y, Z, n), где n – целое положительное число, которое задает количество выделяемых уровней на графике. Если в предыдущем примере заменить последнюю команду на contour (X, Y, Z, 20), то график примет вид, показанный на рисунке 2.27.

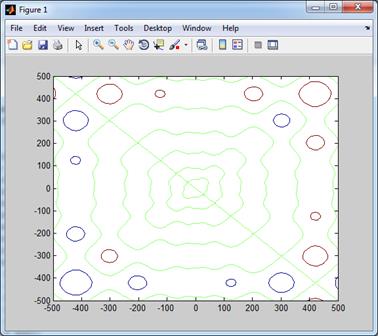
Рис. 2.27.

Кроме того, вместо последнего параметра можно использовать вектор, элементы которого определяют уровни, для которых надо построить линии. Следующий пример рисует три уровня для Z = -500; 0 и 500 (результат показан на рисунке 2.28).

>> meshx = -500: 10: 500;

>> meshy = -500: 10: 500;

>> [X, Y] = meshgrid (meshx, meshy);

>> Z = X .* sin ( sqrt ( abs (X) ) ) + Y .* sin ( sqrt ( abs (Y) ) );

>> contour (X, Y, Z, [-500 0 500])

Рис. 2.28.

Так как матрица размером 1x1 MATLAB воспринимает как число, то для того, чтобы построить одну линию уровня для определенного значения Z, в качестве последнего параметра функции contour нужно передать матрицу размером 2x1, где оба элемента матрицы будут одинаковыми, то есть должны определять один и тот же отображаемый уровень. Например: contour (X, Y, Z, [0, 0]).

Предыдущая 1 2 3 4 567 8 9 10 11 12 13 14 Следующая

Не нашли, что искали? Воспользуйтесь поиском по сайту: