
|
|
Явление дисперсии и групповая скоростьДля случая распространения плоской волны в среде без потерь фазовая скорость не зависит от частоты
Напомним, что зависимость фазовой скорости от частоты называется дисперсией. В этом случае (например, в средах с потерями; в металлических волноводах) при распространении сигнала с конечной полосой частот фазовая скорость не определена и вводится понятие групповой скорости. Существование дисперсии необходимо учитывать, оценивая распространение электромагнитных сигналов – волновых процессов переносящих информацию. Сигналы, как известно, всегда обладают некоторым спектром частот. В дисперсионной среде скорости распространения каждой из гармоник частотного спектра различны (1.36). Поэтому, преодолев некоторое расстояние, эти гармонические составляющие приобретут различные фазовые запаздывания. Сложение этих гармоник с новыми фазовыми сдвигами обязательно приведет к искажению сигнала (формы импульса). Помимо этого, в среде с потерями амплитуда каждой из гармоник затухает по-разному, что также приводит к дополнительным искажениям. Рассмотренное явление обусловлено характеристиками среды, поэтому назовем его материальной дисперсией. Для иллюстрации характеристики групповой скорости рассмотрим распространение двух гармонических сигналов в дисперсионной среде
где величина
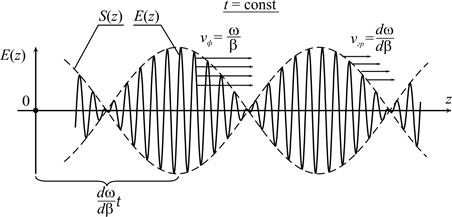
Рис. 3.1. К понятию групповой скорости.
Сигнал (3.2) представлен в виде произведения двух сомножителей – несущей и огибающей, что отражено на рис. 3.1. Скорость распространения огибающей
Групповая скорость совпадает со скоростью распространения энергии, определяемой средним значением вектора Пойнтинга
где для свободного пространства Задания Задание 3.1 Плоская электромагнитная волна с амплитудой
а. f=300 МГц, б. f=300 МГц, в. f=300 МГц, г. f=300 МГц, д. f=500 МГц, е. f=500 МГц, ж. f=500 МГц, з. f=500 МГц, и. f=300 МГц, к. f=300 МГц, л. f=300 МГц, м. f=300 МГц, н. f=500 МГц, о. f=500 МГц, п. f=500 МГц, р. f=500 МГц,
Записать полное пространственно-временное представление для действительного вектора напряжённости электрического поля, предварительно вычислив коэффициенты затухания Решение 3.1а [стр.330, пример(6.15)– (6.16)]
где введены обозначения
Далее
Используем MATLAB и строим зависимости (4) фазовой
clear; clf;
epsr = 9; mur = 1; sigma = 10;
mu0 = 4 * pi * 1e-7; eps0 = 1e-9 / (36 * pi); c = 3e8;
mu = mu0 * mur; eps = eps0 * epsr;
f = 30e6: 10e6: 3e9; omega = 2 .* pi .* f;
v0 = sqrt(1 / (mu * eps)); soe = (sigma ./ (omega * eps)) .^ 2; gct = sqrt(1 + soe); fct = sqrt(1 + gct);
vp = v0 .* sqrt(2) ./ fct; vg = v0 .* sqrt(2) .* fct .* gct ./ (fct .* fct .* gct - 0.5 .* soe);
plot(f / 1e9, vp / c, '-', f / 1e9, vg / c, '--'); grid on; xlabel('f, ГГц'); ylabel('v/c'); legend ('Фазовая скорость', 'Групповая скорость', 2)
Полезно проанализировать два случая 1. Высокочастотная аппроксимация – В этом случае
2. Низкочастотная аппроксимация – В этом случае
Задание 3.2
б. в. г. д. е. ж. з. и. к. л. м.
Рассчитать скин слой для заданной удельной проводимости Решение 3.2а [стр.333, пример(6.17)– (6.18)]
Волна затухает в
При вычислении коэффициенты затухания
В этом случае
Используем MATLAB и строим зависимость (2).
clear; clf;
mu0 = 4 * pi * 1e-7; Ey0 = 10; f = 3e9 sigma = 5.8e7 % Cu delta = 1 / sqrt(pi * f * mu0 * sigma) alpha = 1 / delta; beta = alpha; lambda = 2 * pi / beta z = 0: 0.2e-6: 12e-6; Ey = Ey0 .* exp(-alpha .* z) .* cos(beta .* z);
plot(1e5 * z, Ey); grid on; xlabel('z, мкм'); ylabel('E_x, В/м'); axis ([0 1 -2 10])

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
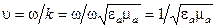 . (3.1)
. (3.1) или
или , (3.2)
, (3.2) играет в сущности ту же роль, что и вещественное k в случае волны в среде без потерь,
играет в сущности ту же роль, что и вещественное k в случае волны в среде без потерь,  –фазовая константа на частоте
–фазовая константа на частоте  .
.
 по аналогии с (3.1) равна
по аналогии с (3.1) равна 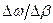 . В пределе
. В пределе  эта скорость распространения огибающей, называемая групповой, равна
эта скорость распространения огибающей, называемая групповой, равна . (3.3)
. (3.3) , (3.4)
, (3.4) ,
, 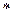 - знак сопряжения.
- знак сопряжения. и частотой f распространяется в положительном направлении оси z в бесконечной среде. Электрическое поле поляризовано по оси x. Параметры среды
и частотой f распространяется в положительном направлении оси z в бесконечной среде. Электрическое поле поляризовано по оси x. Параметры среды 
 :
:

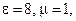



 и фазы
и фазы  . Используя MATLAB, построить зависимости фазовой
. Используя MATLAB, построить зависимости фазовой  и групповой
и групповой  скоростей от частоты в диапазоне 30 < f < 3000 МГц.
скоростей от частоты в диапазоне 30 < f < 3000 МГц. , (1)
, (1) (2)
(2) – тангенс угла диэлектрических потерь,
– тангенс угла диэлектрических потерь, 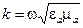 – постоянная распространения среды без потерь,
– постоянная распространения среды без потерь, 
 ;
;  .
. , соответственно
, соответственно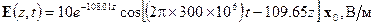 . (3)
. (3) – фазовая скорость;
– фазовая скорость;  – групповая скорость. (4)
– групповая скорость. (4) . (5)
. (5)
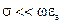 .
. , соответственно
, соответственно . (6)
. (6) .
. , соответственно
, соответственно . (7)
. (7)
 ,
, ; f=3 ГГц
; f=3 ГГц ; f=3 ГГц
; f=3 ГГц f=3 ГГц
f=3 ГГц f=3 ГГц
f=3 ГГц f=3 ГГц
f=3 ГГц f=3 ГГц
f=3 ГГц . Записать пространственное представление для действительной амплитуды
. Записать пространственное представление для действительной амплитуды  электрического поля плоской волны, распространяющейся в заданной среде в момент времени t=0, предварительно вычислив коэффициенты затухания
электрического поля плоской волны, распространяющейся в заданной среде в момент времени t=0, предварительно вычислив коэффициенты затухания  .
. (м)=1.21 мкм. (1)
(м)=1.21 мкм. (1) раз от начальной амплитуды на расстоянии скин-слоя
раз от начальной амплитуды на расстоянии скин-слоя  .
.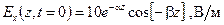 . (2)
. (2) .
.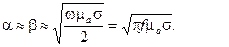 (3)
(3)