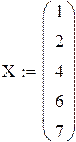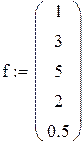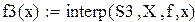|
|
Одной независимой переменнойВ практике вычислений часто требуется определить значение функции f(x), определенной своими значениями f(x0), f(x1), …, f(xn) на определенном наборе точек (узлов)
С помощью этой формулы можно выполнить интерполяцию одной из ветвей входной (например, для Uce = 5 В) или выходной (например, для Ib= 0,3 мА) ВАХ.
Ib, мА Uce = 0В 5В 25В Ic, мА
0,8 40 0,7 мА
0 0,1 0,2 0,3 0,4 0,5 0,6 Ube, В 0 5 10 15 20 25 Uce, В а) б) Рис. 4.1. Входная – а) и выходная – б) ВАХ транзистора типа КТ312Б
Интерполяция таблично заданной функции Двух независимых переменных Предположим, что на некотором наборе узлов на плоскости таблично задана функция двух независимых переменных f(x,y),определенная своими значениями f(x0, y0), f(x1, y1), f(x2, y2)…, f(xn, yn).Примерами функций двух переменных могут служить, представленные на рис. 4.1, зависимости Ib(Uce,Ube)иIc(Uce,Ib). Построение функции F(x,y), позволяющей вычислить значение функции f(x,y)в точках, не совпадающих с заданным набором узлов, называется задачей интерполяции функции двух переменных. При этом f(x,y) называют интерполируемой, а F(x,y) – интерполирующей функциями. Для интерполяции таблично заданной на прямоугольной (k+1)*(m+1) сетке узлов функции двух независимых переменных можно использовать, например, интерполяционную формулу Лагранжа. Однако, при применении интерполяционных полиномов для выполнения интерполяции возможно появление явления волнистости, при котором значение интерполирующей функции между узлами сколь угодно сильно отличается (осциллирует) от значений интерполируемой функции в близлежащих узлах. Это является свойством степенного полинома. Так как явление волнистости не проявляется для полиномов степени три и менее, то для его преодоления используют линейную, квадратичную или кубическую сплайн-интерполяцию.
Сплайн-интерполяция
Функция одной переменной S(x), заданная на отрезке [a, b], называется сплайном порядка p, если она: 1. На каждом из частичных отрезков 2. р-1 раз непрерывно дифференцируема на [a, b].При сплайн-интерполяции интерполируемая функция представляется набором полиномов первой, второй или третьей степени соответственно – своим для каждого из внутренних подотрезков Для реализации одномерной и двумерной сплайн-интерполяции в пакете Mathcad имеются следующие функции: · interp(vs,Mx,My,x) – возвращает значение, найденное сплайн-интерполяцией для заданных параметров vs, Mx, My и x, где Mxи My −матрицы входных данных; vs −выходной вектор функций cspline, pspline или lspline; x − вектор размерности n · cspline(Mx,My) –возвращает вектор вторых производных (первый из аргументов в функции interp(vs,Mx,My,x)) по исходным данным Mx (матрица размерности n · pspline(Mx,My) -возвращает вектор вторых производных (первый из аргументов в функции interp(vs,Mx,My,x)) по исходным данным Mx (матрица размерности n · lspline(Mx,My) -возвращает вектор вторых производных (первый из аргументов в функции interp(vs,Mx,My,x)) по исходным данным Mx (матрица размерности n На рис. 4.2 для случая функции одной независимой переменной f(x) показана программа для Mathcad, реализующая кубическую сплайн-интерполяцию, а на рис. 4.3 − соответствующая программа для Mathcad, реализующая кубическую сплайн-интерполяцию для функции двух переменных.
Рис. 4.2. Реализация кубической сплайн-интерполяция функции одной переменной в пакете Mathcad 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
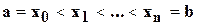 , в некоторой промежуточной точке
, в некоторой промежуточной точке 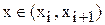 , где i=0, 1, … , n-1. Построение функции F(x), позволяющей вычислить значение функции f(x)в точках, не совпадающих с заданным набором узлов, называется задачей интерполяции функции одной переменной. При этом f(x) называют интерполируемой, а F(x) – интерполирующей функциями. Определение значения функции f(x) для x<a или x>b, называется задачей экстраполяции. При решении этих двух задач часто используются интерполяционная формула Лагранжа для неравноотстоящих узлов, приведенная ниже
, где i=0, 1, … , n-1. Построение функции F(x), позволяющей вычислить значение функции f(x)в точках, не совпадающих с заданным набором узлов, называется задачей интерполяции функции одной переменной. При этом f(x) называют интерполируемой, а F(x) – интерполирующей функциями. Определение значения функции f(x) для x<a или x>b, называется задачей экстраполяции. При решении этих двух задач часто используются интерполяционная формула Лагранжа для неравноотстоящих узлов, приведенная ниже .
.






 Ib=
Ib=
 0,6 мА
0,6 мА



 0,6 30 0,5 мА
0,6 30 0,5 мА
 0,4 мА
0,4 мА

 0,2 мА
0,2 мА

 0,2 10 0,1 мА
0,2 10 0,1 мА

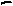
 , i = 0, 1, …, n-1 заданной степени
, i = 0, 1, …, n-1 заданной степени  , то есть может быть записана как
, то есть может быть записана как  .
.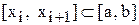 .
. 1.
1.