|
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Выполнить анализ нелинейной цепи (рис. 3.4). Искомыми являются напряжения на резисторе и диоде. Исходные данные и тип интерполяционного полинома в соответствии с вариантом.
Исходные данные и тип интерполяционного полинома
для анализа нелинейной цепи (не для печати)
| N вар.
| Векторы значений
| Тип полинома
| E,
В
| R, Ом
| | напряжения
| тока
| |
| [0.2, 0.4, 0.5]-1
| [0, 0.01, 0.04]-1
| степенной
|
|
| |
| [0.35, 0.5]-1
| [0.04, 0.6]-1
| экспоненциальный
|
|
| |
| [0.4, 0.6, 0.8]-1
| [0.002, 0.007, 0.017]-1
| степенной
|
|
| |
| [0.5, 0.7]-1
| [0.01, 5]-1
| экспоненциальный
|
|
| |
| [0.2, 0.4, 0.6]-1
| [0.0, 0.1, 0.26]-1
| степенной
|
|
| |
| [0.4, 0.6]-1
| [0.02, 0.065]-1
| экспоненциальный
|
|
| |
| [0.4, 0.6, 0.8]-1
| [0.02, 0.06, 0.14]-1
| степенной
|
|
| |
| [0.4, 0.8]-1
| [0.01, 0.06]-1
| экспоненциальный
| 1.5
|
| |
| [0.3, 0.4, 0.5]-1
| [0.003, 0.01, 0.04]-1
| степенной
|
|
| |
| [0.2, 0.4]-1
| [0.0005, 0.0035]-1
| экспоненциальный
|
|
| | a
| [0.2, 0.5]-1
| [0.01, 0.04]-1
| экспоненциальный
|
|
| | b
| [0.35, 0.5]-1
| [0.04, 0.6]-1
| степенной
|
|
| | c
| [0.4, 0.8]-1
| [0.002, 0.017]-1
| экспоненциальный
|
|
| | d
| [0.5, 0.6, 0.7]-1
| [0.01, 1, 5]-1
| степенной
|
|
| | e
| [0.2, 0.6]-1
| [0.01, 0.26]-1
| экспоненциальный
|
|
| | f
| [0.4, 0.5, 0.6]-1
| [0.02, 0.04, 0.065]-1
| степенной
|
|
|
2. Найти численное решение задачи Коши для дифференциального уравнения 1-го порядка на отрезке [x0, x0+1].
Условия задачи Коши для дифференциального уравнения 1-го порядка
(не дл печати)
| N вар.
| y’=f(x,y), y(x0)=y0
| N вар.
| y’=f(x,y), y(x0)=y0
| |
| y’=y2+x2, y(0)=0.5
|
| y’=y-x, y(0)=1
| |
| y’=cos(x+y), y(0)=0
|
| y’=1+x-y2, y(0)=1
| |
| y’=e-y+x2, y(1)=0
| a
| y’=x3+y2, y(0)=0.5
| |
| y’=x ln(y), y(1)=1
| b
| y’=2.x+cos(y), y(0)=0
| |
| y’=x.y+8, y(0)=0
| c
| y’=ex-y2, y(0)=0
| |
|  , y(1)=e , y(1)=e
| d
|  , , 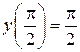
| |
| 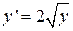 , y(0)=1 , y(0)=1
| e
|  , y(0)=1 , y(0)=1
| |
|  , , 
| f
|  , , 
|
3. Найти решение задачи Коши для системы дифференциальных уравнений 1-го порядка
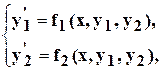  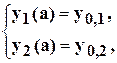
на отрезке [a, b] с постоянным шагом h=0.1. Изобразить график найденного решения.
Условия задачи Коши для системы
дифференциальных уравнений 1-го порядка (не для печати)
| N вар.
| f1(x,y1,y2)
| f2(x,y1,y2)
| y1(a)
| y2(a)
| a
| b
| |
| 
| 
| 0.5
| 1.5
|
|
| |
| 
| 
| -1
|
|
|
| |
| 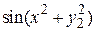
| 
|
|
|
|
| |
| 
| 
| -0.6
|
|
|
| |
| 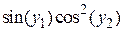
| 
|
|
| -1
|
| |
| 
| 
|
|
|
|
| |
| 
| 
|
|
|
|
| |
| 
| 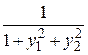
|
|
|
|
| |
| 
| 
|
|
| -2
|
| |
| 
| 
| -1
|
|
|
| | a
| 
| 
|
|
|
|
| | b
| 
| 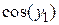
| 0.5
| -0.5
| -1
|
| | c
| 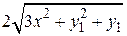
| 
| 0.5
| 1.2
|
|
| | d
| 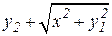
| 
| 0.8
| 3.5
|
|
| | e
| 
| 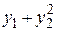
| -2
| -1
|
|
| | f
| 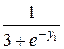
| 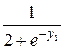
|
| -3
|
|
|
4. Выполнить анализ (в данном случае это поиск 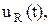  ) или ) или 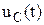 во временном диапазоне от 0 и до Т области одной из схем рис. 3.8 (для нечётных вариантов − схема рис. 3.8,а, для чётных − схема рис. 3.8,б). Для задания начальных условий следует использовать знания, полученные при изучении физики. При составлении выражения для вычисления функции во временном диапазоне от 0 и до Т области одной из схем рис. 3.8 (для нечётных вариантов − схема рис. 3.8,а, для чётных − схема рис. 3.8,б). Для задания начальных условий следует использовать знания, полученные при изучении физики. При составлении выражения для вычисления функции  рекомендуется использовать, известное из аналитической геометрии уравнение прямой линии, проходящей через две заданные точки. рекомендуется использовать, известное из аналитической геометрии уравнение прямой линии, проходящей через две заданные точки.
Вид входных сигналов при анализе переходных процессов (не для печати)
Вид 
| Параметры
| Вид 
| Параметры
| Вариант 0
 
    10 10
 3 3
  0 t
0 0 t
0   Т Т
|  =10 мкс =10 мкс
 =20 мкс
Т=30 мкс
R=50 Ом
L=0,1 мГн
C=12 нФ =20 мкс
Т=30 мкс
R=50 Ом
L=0,1 мГн
C=12 нФ
| Вариант 8
 
    2 2
 0 t 0 t
  T T
  -2 -2
|  =1 мс =1 мс
 =2 мс
Т=3,5 мс
R=200 Ом
L=20 мГн
C=800 нФ =2 мс
Т=3,5 мс
R=200 Ом
L=20 мГн
C=800 нФ
| Вариант 1
 
   5
0 5
0  t
0 t
0   T T
|  =5 мс =5 мс
 =20 мс
Т=40 мс
R=150 Ом
L=0,2 Гн
C=20 мкФ =20 мс
Т=40 мс
R=150 Ом
L=0,2 Гн
C=20 мкФ
| Вариант 9
 
   5 5
 0 t
0 0 t
0   T T
|  =5 мс =5 мс
 =20 мс
Т=40 мс
R=150 Ом
L=0,2 Гн
C=20 мкФ =20 мс
Т=40 мс
R=150 Ом
L=0,2 Гн
C=20 мкФ
| Вариант 2
 
  20 20
   7 7
  0 t
0 0 t
0   Т Т
|  =6 нс =6 нс
 =15 нс
Т=35 нс
R=1 кОм
L=1 мкГн
C=3 пФ =15 нс
Т=35 нс
R=1 кОм
L=1 мкГн
C=3 пФ
| Вариант a
  0
0    t t
  T
-15 T
-15
 
|  =100 нс =100 нс
 =200 нс
Т=650 нс
R=5 Ом
L=600 нГн
C=12 нФ =200 нс
Т=650 нс
R=5 Ом
L=600 нГн
C=12 нФ
| Вариант 3
 
   0 t 0 t
 -5 -5   Т Т
-20

|  =6 нс =6 нс
 =15 нс
Т=40 нс
R=150 Ом
L=1 мкГн
C=30 пФ =15 нс
Т=40 нс
R=150 Ом
L=1 мкГн
C=30 пФ
| Вариант b
 
   0 t 0 t
  -25 -25   T T

 -50 -50
|  =0,1 мс =0,1 мс
 =0,2 мс
Т=0,35 мс
R=20 Ом
L=0,4 мГн
C=400 нФ =0,2 мс
Т=0,35 мс
R=20 Ом
L=0,4 мГн
C=400 нФ
| Вариант 4
 
   20 20
  0 t
0 0 t
0   Т Т
|  =15 мкс =15 мкс
 =20 мкс
Т=50 мкс
R=25 Ом
L=80 мкГн
C=100 нФ =20 мкс
Т=50 мкс
R=25 Ом
L=80 мкГн
C=100 нФ
| Вариант c
  1
1
   0 t 0 t
  T T
 -25 -25
|  =15 мкс =15 мкс
 =40 мкс
Т=250 мкс
R=250 Ом
L=9 мГн
C=100 нФ =40 мкс
Т=250 мкс
R=250 Ом
L=9 мГн
C=100 нФ
| Вариант 5
 
 20 20

  7 7
  0 t
0 0 t
0   Т Т
|  =6 нс =6 нс
 =15 нс
Т=35 нс
R=1 кОм
L=1 мкГн
C=3 пФ =15 нс
Т=35 нс
R=1 кОм
L=1 мкГн
C=3 пФ
| Вариант d
  2
2     t t
  T
-15 T
-15
 
|  =100 нс =100 нс
 =200 нс
Т=650 нс
R=5 Ом
L=600 нГн
C=12 нФ =200 нс
Т=650 нс
R=5 Ом
L=600 нГн
C=12 нФ
| Вариант 6
 
   0 t
-5 0 t
-5   Т Т
 -20
-20

|  =6 нс =6 нс
 =15 нс
Т=40 нс
R=150 Ом
L=1 мкГн
C=30 пФ =15 нс
Т=40 нс
R=150 Ом
L=1 мкГн
C=30 пФ
| Вариант e
 
   0 t 0 t
  -25 -25   T T
 -50 -50
|  =0,1 мс =0,1 мс
 =0,2 мс
Т=0,35 мс
R=20 Ом
L=0,4 мГн
C=400 нФ =0,2 мс
Т=0,35 мс
R=20 Ом
L=0,4 мГн
C=400 нФ
| Вариант 7
 
   20 20
   0 t
0 0 t
0   Т Т
|  =15 мкс =15 мкс
 =20 мкс
Т=50 мкс
R=25 Ом
L=80 мкГн
C=100 нФ =20 мкс
Т=50 мкс
R=25 Ом
L=80 мкГн
C=100 нФ
| Вариант f
  3
3
   0 t 0 t
  T T
 -25 -25
|  =15 мкс =15 мкс
 =40 мкс
Т=250 мкс
R=250 Ом
L=9 мГн
C=100 нФ =40 мкс
Т=250 мкс
R=250 Ом
L=9 мГн
C=100 нФ
|
5. Выполнить анализ во временном диапазоне от 0 и до Т области одной из схем рис. 3.13 (для чётных вариантов − схема рис. 3.13,а, для нечётных − схема рис. 3.13,б).
???
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Сформулируйте задачу Коши для ОДУ 1-го и n-ого порядков, а также для системы ОДУ 1-го порядка.
2. Как решается в системе MatLab ОДУ n-ого порядка?
3. Изобразите простейшие электронные цепи, анализ которых может быть выполнен с использованием ОДУ 1-го порядка. Запишите уравнения, описывающие эти цепи.
4. Изобразите простые электронные цепи, анализ которых может быть выполнен с использованием ОДУ 2-го порядка. Запишите уравнения, описывающие эти цепи.
ЛАБОРАТОРНАЯ РАБОТА № 4
Применение интерполяционных методов
Для приближения ВАХ транзистора
ЦЕЛЬ РАБОТЫ
Ознакомление с особенностями выполнения интерполяции и сплайн-интерполяции с использованием пакета Mathcad.
ПОЯСНЕНИЯ К РАБОТЕ
Введение
Базовыми при проектировании многих радиотехнических устройств на транзисторах являются его входная Ib(Ube, Uce) и выходная Ic(Uce, Ib) вольт-амперные характеристики (ВАХ), показанные на рис. 4.1, где Ib –ток базы, Ube –напряжение база-эммитер,Uce – напряжение коллектор-эммитер, Ic– ток коллектора. Поэтому вопросы приближения этих характеристик являются весьма актуальными в инженерной практике.
Интерполяция таблично заданной функции
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , y(1)=e
, y(1)=e
 ,
, 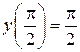
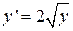 , y(0)=1
, y(0)=1
 , y(0)=1
, y(0)=1
 ,
, 
 ,
, 
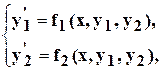

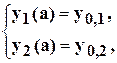




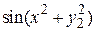



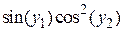






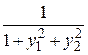







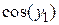
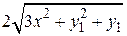

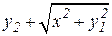


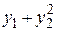
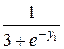
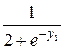
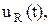
 ) или
) или 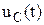 во временном диапазоне от 0 и до Т области одной из схем рис. 3.8 (для нечётных вариантов − схема рис. 3.8,а, для чётных − схема рис. 3.8,б). Для задания начальных условий следует использовать знания, полученные при изучении физики. При составлении выражения для вычисления функции
во временном диапазоне от 0 и до Т области одной из схем рис. 3.8 (для нечётных вариантов − схема рис. 3.8,а, для чётных − схема рис. 3.8,б). Для задания начальных условий следует использовать знания, полученные при изучении физики. При составлении выражения для вычисления функции  рекомендуется использовать, известное из аналитической геометрии уравнение прямой линии, проходящей через две заданные точки.
рекомендуется использовать, известное из аналитической геометрии уравнение прямой линии, проходящей через две заданные точки.



 10
10
 3
3

 0 t
0
0 t
0 
 Т
Т





 2
2
 0 t
0 t

 -2
-2






 0 t
0
0 t
0 

 20
20


 7
7

 0 t
0
0 t
0 


 t
t




 0 t
0 t




 0 t
0 t


 -50
-50


 20
20




 0 t
0 t -25
-25 20
20





 -20
-20



 -25
-25