|
|
Некоторые из основных приемов работы В MatLABПервое знакомство с Математическим Пакетом Matlab
ЦЕЛЬ РАБОТЫ Ознакомление с программным пакетом для математических расчетов MatLab R2007bи получение первоначальных навыков его использования.
1.1. ПОЯСНЕНИЯ К РАБОТЕ
Введение
MatLab – это мощное и универсальное программное средство решения задач, возникающих в различных областях человеческой деятельности. Его можно использовать при: матричном анализе, обработке сигналов и изображений, решении задач математической физики и оптимизационных задач, обработке и визуализации данных, работе с картографическими изображениями и многом другим.
Пользовательский интерфейс Запуск MatLab R2007bпроизводится стандартным для Windows способом. Типичный вид экрана монитора при работе с MatLab R2007b показан на рис. 1.1. Для установки вида окна, принятого по умолчанию, следует ЛКМ выбрать меню Desktop
  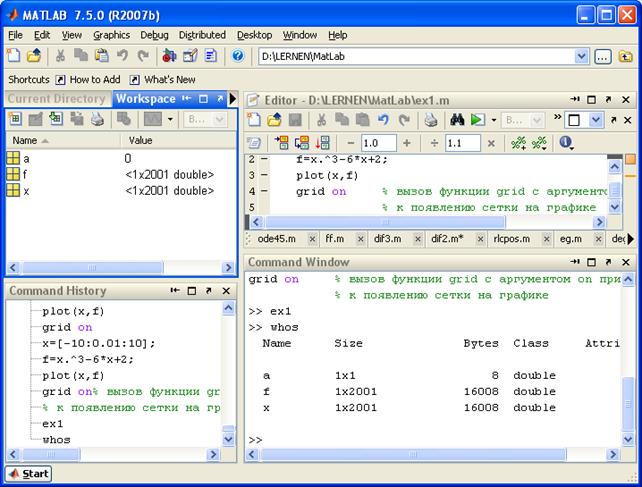
Рис. 1.1. Рабочее окно MatLab R2007b
Ограничимся рассмотрением только тех пунктов меню, которые не являются стандартными для Windows и представляют наибольший интерес при выполнении (в рамках настоящих методических указаний) математического моделирования радиотехнических цепей и процессов в них. Меню File Пункты Clear Command Window, Clear Command History и Clear Workspace в меню Edit позволяют очистить соответственно командное окно, окно истории команд и окно переменных. Окно переменных позволяет быстро и просто получить информацию не только о доступных переменных, но и проконтролировать их значения (двойным щелчком ЛКМ). Окно История команд удобно тем, что позволяет быстро найти, вызвать, скопировать или удалить ранее уже набранную команду. В Окне команд содержится перечень последних поданных команд, результаты их выполнения и служебные сообщения. ???????
Некоторые из основных приемов работы В MatLAB
В MatLab используются все буквы латинского алфавита и арабские цифры от 0 до 9. Как и в С++, большие и малые буквы различаются. Кроме букв латинского алфавита используются все специальные символы клавиатуры компьютера. Все символы после символа ‘%’ до конца текущей строки в MatLab рассматриваются как комментарии. Выполнение арифметических вычислений.Используются символы: `+`, `-`, `*`, `/` и `^` (возведение в степень). Для установления приоритета выполнения действий следует использовать круглые скобки `()`, а для подавления печати результата вычислений необходимо применять символ `;`. Пусть необходимо вычислить следующее выражение Щёлкнем ЛКМ в командной строке (там после этого должен появиться мигающий курсор) и наберем следующую последовательность символов 2^3.2/4.7-4*5.6 и нажмите на клавишу <<Enter>>. В рабочем окне появится запись
>> 2^3.2/4.7-4*5.6
ans =
-20.4448
>>
− к конце которой будет расположен мигающий курсор. Если набрать следующую последовательность символов 2^3.2/4.7-4*5.6; и тоже нажать на клавишу <<Enter>>, то в рабочем окне появится другая запись
>> 2^3.2/4.7-4*5.6; >>
− с мигающим курсором в конце. Печать результата вычислений здесь подавлена символом `;`. Он хранится в переменной с именем ans и для его получения следует в командной строке набрать ans<<Enter>>. Кроме того в дальнейших вычислениях имя этой переменной (ans) можно подставлять вместо результата вычислений. Если имеется необходимость повторно вызвать ранее уже введённую запись, то это легче всего сделать, используя клавиши << Вообще говоря, имя переменной может состоять из букв латинского алфавита, знака подчёркивания и цифр, и обязательно должно начинаться с буквы. Для того чтобы проверить занято ли уже какое-либо имя следует набрать в командной строке exist(‘имя переменной’). Нулевой ответ при выполнении этой команды (вызова функции exist) говорит, что имя свободно. Пример.
>> exist('a6')
ans =
Для изменения формата выводимых числовых данных можно поступить двумя способами. Первый состоит в вызове в командной строке функции format с одним из её аргументов: short, short e, long, long e, bank, compact, loose. Пример
>> format short
Второй способ состоит в вызове (ЛКМ через меню File
Рис. 1.2. Окно Preferences
Массивы и работа с ними.Все данные MatLab представляет в виде массивов. Простое число в MatLab представляется в виде двумерного массива размером один на один. Массив − это упорядоченная, пронумерованная совокупность однородных данных, имеющая имя. Массивы бывают одномерными (вектор-столбцы и вектор-строки), двумерные и многомерные. В MatLabнумерация элементов массивов начинается с единицы. Ввод вектор-строки осуществляется в квадратных скобках. При этом элементы следует отделять друг от друга пробелом или запятой. Пример
>> a=[0.8 2.3 9.1] a = 8.0000e-001 2.3000e+000 9.1000e+000
Ввод вектор-столбца также осуществляется в квадратных скобках, но при этом элементы отделяются друг от друга точкой с запятой. Пример
>> b=[-2.2;5.9;0.7] b = -2.2000e+000 5.9000e+000 7.0000e-001
Над векторами определены следующие операции: вычисления его длины, транспонирования, сложения, вычитания, умножения на число, скалярное и векторное (только для трёхэлементных векторов) произведения, как показано ниже
>> L=length(a) % вычисление длины вектора L = >> ar=a' % транспонирование вектора ar = 0.8000 2.3000 9.1000 >> c=[0.2 0.7 0.9]; >> d=a+c % вычисление суммы векторов d = 1 3 10 >> g=a-c % вычисление разности векторов g = 0.6000 1.6000 8.2000 >> z=a*2 % умножение вектора на число z = 1.6000 4.6000 18.2000 >> u=dot(a,c) % скалярное умножение векторов u = 9.9600 >> y=cross(a,c) % векторное умножение векторов y = -4.3000 1.1000 0.1000
Векторы могут быть элементами при определении новых векторов, например
>> ac=[a,c] ac = 0.8000 2.3000 9.1000 0.2000 0.7000 0.9000 >> act=[ar;c'] act = 0.8000 2.3000 9.1000 0.2000 0.7000 0.9000
Для доступа к элементу массива следует после имени массива в круглых скобках указать его индекс, например
>> act(3)+y(1) ans = 4.8000
При работе с индексами удобна индексация при помощи символа ‘:’. Примеры
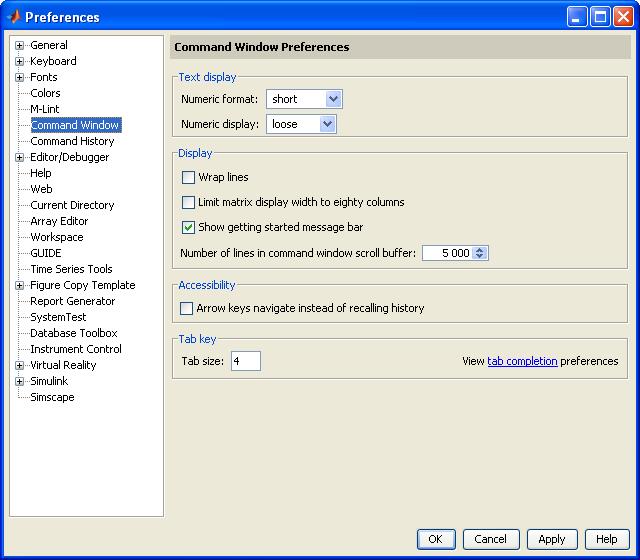
>> act(2:5)=0 act = 0.8000 0.9000 >> x=0:2*pi/9:2*pi % начальное значение 0, шаг − x = Columns 1 through 9 0 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 4.8869 5.5851 Column 10 6.2832
Над векторами возможны так называемые поэлементные операции (поэлементные умножение, деление и возведение в степень), как показано ниже
>> v=a.*c % поэлементное умножение v = 0.1600 1.6100 8.1900 >> z=a./c % поэлементное деление z = 4.0000 3.2857 10.1111 >> s=a.^c % поэлементное возведение в степень s = 0.9564 1.7915 7.2969
В системе MatLab не определены поэлементное сложение и вычитание. Ввод двумерных массивов (прямоугольных матриц) осуществляется по строкам. Пусть, например, необходимо ввести матрицу
Это можно сделать тремя способами:
>> A=[0.4 -4.5 8.3;6.8 0.9 1.1; -6.3 3.5 4.7] % отделяем строки символом ‘;’ A = 0.4000 -4.5000 8.3000 6.8000 0.9000 1.1000 -6.3000 3.5000 4.7000 B=[ 1.3 5.2 -8.1<<Enter>> % отделяем строки нажатием -1.7 2.4 0.3<<Enter>> % на клавишу <<Enter>> 6.6 -7.1 1.0]<<Enter>> B = 1.3000 5.2000 -8.1000 -1.7000 2.4000 0.3000 6.6000 -7.1000 1.0000 >> D=[[3;4] [-1;3] [6;0]] % элементами строки являются столбцы D = 3 -1 6 4 3 0
Над матрицами определены следующие операции: вычисление размера матрицы, вычисление числа элементов матрицы, транспонирование, сложение и вычитание матриц (как для векторов), умножение на число (также как и для векторов), а также матричное произведение и возведение в степень (для квадратных матриц), как показано ниже
>> C=[4.4 0.7 -0.6; 2.8 -0.1 5.6] % ввод матрицы C = 4.4000 0.7000 -0.6000 2.8000 -0.1000 5.6000 >> s=size(C) % вычисление размера матрицы s = 2 3 >> C1=C.' % транспонирование матрицы C1 = 4.4000 2.8000 0.7000 -0.1000 -0.6000 5.6000 >> n=numel(A) % вычисление числа элементов в матрице n = >> P=A*B % матричное произведение P = 62.9500 -67.6500 3.7100 14.5700 29.7100 -53.7100 16.8800 -57.7300 56.7800 >> PP=A^2 % возведение в степень PP = -82.7300 23.2000 37.3800 1.9100 -25.9400 62.6000 -8.3300 47.9500 -26.3500
Обращение к элементам матрицы выполняется аналогично обращению к элементам вектора, но с использованием запятой, например
>> C(2,2)=-10 % элементу присваивается значение C = 4.4000 0.7000 -0.6000 2.8000 -10.0000 5.6000 >> c121=C(1:2,1) % выделяются элементы С(1,1) и С(2,1) c121 = 4.4000 2.8000 >> PP(:,2)=[] % удаляется второй столбец PP = -82.7300 37.3800 1.9100 62.6000 -8.3300 -26.3500 >> PP(:,3)=[1 2 3] % добавляется третий столбец PP = -82.7300 37.3800 1.0000 1.9100 62.6000 2.0000 -8.3300 -26.3500 3.0000
Для матриц, как и для векторов, определены следующие поэлементные операции: A.*B − поэлементные умножения; A./B − поэлементные деления; A.^p − поэлементное возведение в степень (p − число); A.^B − возведение элементов матрицы A в степени, равные соответствующим элементам матрицы B. Элементарные функции системы MatLab. MatLab включает в себя огромный набор функций. Для знакомства с ними и выбора необходимой следует воспользоваться справочной службой системы через меню Help
Рис. 1.3. Окно справочной системы
Построение таблицы значений функции пользователя.Пусть необходимо построить таблицу значений функции 1. Создаётся вектор-строка х, которая содержит координаты требуемых точек. 2. Для каждого элемента вектора х вычисляется значение функции y(x) и полученное значение записывается в вектор-строку − как показано ниже (операции умножения, деления и возведения в степень в выражении для функции должны выполняться поэлементно!)
>> x=[0.1:0.3:2.5] x = 0.1000 0.4000 0.7000 1.0000 1.3000 1.6000 1.9000 2.2000 2.5000 >> y=sin(x).^3./(1-0.5*cos(x))+exp(-x).*log10(x) y = -0.9029 -0.1573 0.3560 0.8164 1.0638 1.0256 0.7712 0.4463 0.1857
Построение графика функции.Если в следующей строке командного окна вызвать функцию plot(x,y), то откроется окно, показанное на рис. 1.4, с искомым графиком.
Рис. 1.4. Окно графика
Для того, чтобы на одной координатной плоскости построить графики двух функций (например, y(x) и sin(3x)) следует вызвать функцию plot со следующим списком аргументов
>> plot(x,y,x,sin(3*x))
После выполнения сказанного вид окна графика приобретёт вид, представленный на рис. 1.5. Если желательно, чтобы графики кривых не выглядели ломанными, то необходимо при определении вектора х выбрать меньший шаг.
Рис. 1.5. Окно графика
Функция plot позволяет пользователю достаточно гибко управлять процессом визуализации результатов вычислений. Один из возможных её синтаксисов plot(X1,Y1,LineSpec1,X2,Y2,LineSpec2,...), где Х1, Х2, … − имена векторов оси абсцисс; Y1, Y2, … − имена векторов оси ординат; LineSpec1, LineSpec2, … − спецификации 1-ой, 2-ой и т. д. линий, записываемы в апострофах (см. таблицу 1.1). Пример
>> x1=[0:0.01:2:pi]; >> t3=[-pi:0.05:pi]; >> r1=exp(-x1).*sin(x1); >> w4=t3.^2.*cos(t3); >> plot(x1,r1,'r*',t3,w4,'k--')
Записанное выше приведёт к построению графика, показанного на рис. 1.6. Таблица 1.1
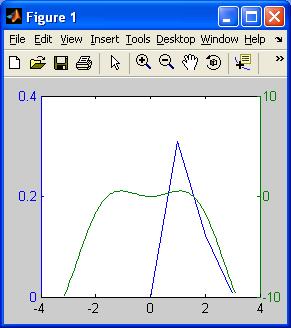
>> plotyy(x1,r1,t3,w4)
Рис. 1.6. Окно графика Из рассмотрения этого рисунка видно, что значения двух функций сильно отличаются по величине и для них желательно иметь несколько отличающиеся оси ординат. Последнее достигается использованием функции (результат − на рис. 1.7)
Рис. 1.7. Окно графика
М-файл функции.Работа из командной строки MatLab вызывает затруднения, если требуется вводить много команд и часто их изменять. Пусть, например, необходимо так задать в MatLab функцию
Рис. 1.8. Окно редактора М-файлов с функцией
Теперь имеется возможность вызывать функцию f, указывая конкретное значение её параметра, например
>> f(7) ans =
Если имеется необходимость повторно вызвать функцию f, то это целесообразно сделать, используя клавиши << Построим график приведенной выше функции f(x) в декартовых координатах для промежутка изменения аргумента [-0.2, 2] с шагом 0.2. Будем исходить из того, что М-файл для f(x)уже сохранён на диске. Подадим в командной строке две простые команды
>> x=[-0.2:0.2:2]; >> plot(x,f(x))
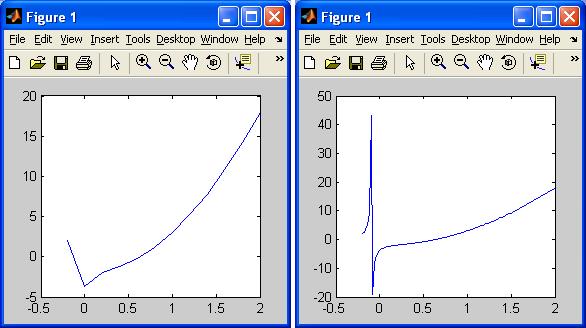
Результатом этих действий будет график, представленный на рис. 1.9,а. Если же подать следующие две команды
>> x=[-0.2:0.02:2]; >> plot(x,f(x))
то результат окажется несколько иным (см. рис. 1.9,б).
а) б) Рис. 1.9. Окна графика функции f(x)
Решение системы линейных алгебраических уравнений (СЛАУ). Постановка задачи. Общий вид у СЛАУ следующий:
В матричном виде эта СЛАУ может быть записана в виде:
называется матрицей системы, Справедливо следующее утверждение. Если определитель Рассмотрим порядок решения СЛАУ в MatLab на конкретном примере. Найти решение СЛАУ вида
Процесс решения будет выглядеть следующим образом
>> A=[7.9 5.6 5.7 -7.2;8.5 -4.8 0.8 3.5;4.3 4.2 -3.2 9.3;3.2 -1.4 -8.9 3.3] A = 7.9000 5.6000 5.7000 -7.2000 8.5000 -4.8000 0.8000 3.5000 4.3000 4.2000 -3.2000 9.3000 3.2000 -1.4000 -8.9000 3.3000 >> det(A) ans = -1.0178e+004 % det А не равен нулю − решение единственное >> b=[6.68;9.95;8.6;1] b = 6.6800 9.9500 8.6000 1.0000 >> x=A\b x = 0.9671 0.1248 0.4263 0.5679 >> A*x-b % вычисление невязки ans = 1.0e-014 * -0.0888 0.1776 0.1776 0.0444
Символ ‘\’ является оператором решения систем линейных уравнений. Решение нелинейного уравнения.Нелинейным уравнением называется выражение вида Функция К численным методам решения нелинейных уравнений приходиться обращаться в случае отсутствия у них аналитических выражений для решений или же если выполнение вычислений по ним является крайне трудоёмким делом. Приближенное нахождение изолированных действительных корней обычно складывается из двух этапов: 1. отделение корней, т. е. нахождение возможно узких промежутков 2. уточнение приближенных корней, т. е. нахождение их положения с заданной степени абсолютной точности Для отделения корней полезна известная теорема существования корней нелинейного уравнения из математического анализа. Теорема. Если непрерывная функция Корень Пример 1. Отделить корни уравнения Решение.
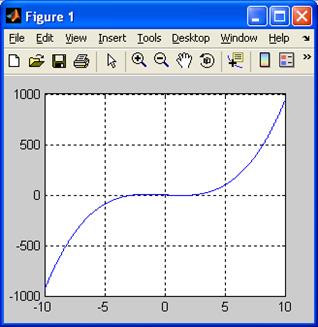
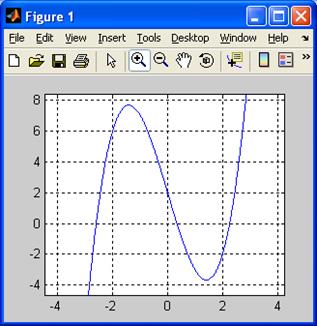
>> x=[-10:0.01:10]; >> f=x.^3-6*x+2; >> plot(x,f) >> grid on % вызов функции grid с аргументом on приводит % к появлению сетки на графике Результат представлен на рис. 1.10,а. На нём видно, что у уравнения действительно имеется хотя бы один корень, но для более чёткого отделения корней желательно увеличить ту часть рисунка, что прилегает к оси абсцисс. Для этой цели следует использовать инструменты
а) б) Рис. 1.10. Отделение корней нелинейного уравнения
Для реализации второго этапа решения нелинейного уравнения вида − fzero(‘fun’,x) − возвращает уточнённое значение для х, при котором достигается нуль функции fun − имя М-файла, представленной строкой. х, стоящее вторым аргументом при вызове fzero, является начальным приближением к искомому корню. Примеры
>> fzero('cos',1) ans = 1.5708
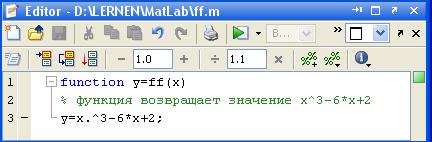
>> fzero('ff',-3) ans = -2.6017
В втором примере ff − это имя функции пользователя, которая должна быть оформлена в виде М-файла (см. рис. 1.11).
Рис. 1.11. Окно редактора М-файлов с функцией ff
− fzero(‘fun’,[x1 x2]) − возвращает уточнённое значение для х, находящееся внутри интервала (х1, х2). Должно выполняться условие fun(x1)×fun(x2) < 0. Примеры
>> fzero('ff',[-3 -2]) ans = -2.6017 >> fzero('ff',[0,1]) ans = 0.3399
− fzero(‘fun’,x,tol), fzero(‘fun’,[x1 x2], tol) − выполняют те же действия, что и ранее, но с заданной относительной точностью tol. Примеры
>> format long >> fzero('ff',-3,1e-15) ans = -2.601679131883155 >> fzero('ff',[0,1],1e-10) ans = 0.339876886623182
В зависимости от используемой формы функции fzero, MatLab реализует следующие методы поиска корня уравнения: метод дихотомии, метод секущих или метод обратной квадратичной интерполяции.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Desktop Layout
Desktop Layout 


 Preferences… предоставляет возможность пользователю устанавливать параметры рабочей среды. Меню File
Preferences… предоставляет возможность пользователю устанавливать параметры рабочей среды. Меню File 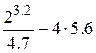 .
.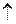 >> и <<
>> и <<  >>.
>>.
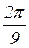 , конечное −
, конечное − 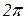
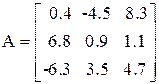 .
.
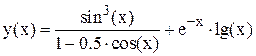 для значений переменной х от 0.1 и до 2.5 с шагом 0.3. Требуемое выполняется в два этапа.
для значений переменной х от 0.1 и до 2.5 с шагом 0.3. Требуемое выполняется в два этапа.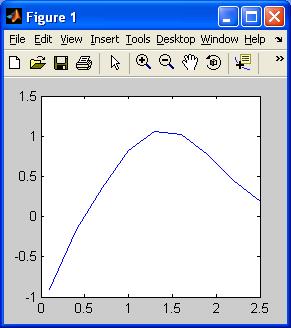


 , чтобы в дальнейшем её значение для, например, х = 7, можно было бы получить простым вызовом f(7) в командной строке − также как и для элементарных функций. Для этого в MatLab имеется простой механизм, называемый М-файл функция. Это, в сущности, аналог функций языков программирования. Сначала М-файл функцию надо создать. Для этого необходимо выполним щелчёк ЛКМ по иконке
, чтобы в дальнейшем её значение для, например, х = 7, можно было бы получить простым вызовом f(7) в командной строке − также как и для элементарных функций. Для этого в MatLab имеется простой механизм, называемый М-файл функция. Это, в сущности, аналог функций языков программирования. Сначала М-файл функцию надо создать. Для этого необходимо выполним щелчёк ЛКМ по иконке  (New M-File − новый М-файл), находящейся в панели ярлыков (то же самое можно сделать выбрав меню File
(New M-File − новый М-файл), находящейся в панели ярлыков (то же самое можно сделать выбрав меню File 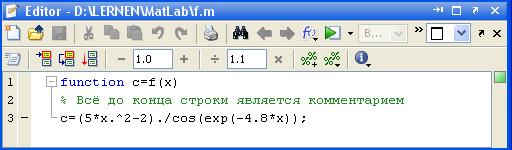

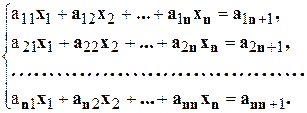 .
. , где
, где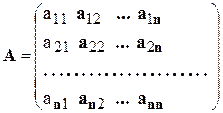
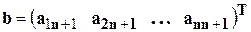 − вектор-столбцом свободных членов или правых частей системы, а
− вектор-столбцом свободных членов или правых частей системы, а 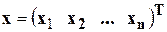 − искомым вектор-столбцом неизвестных системы. Решением СЛАУ является всякий вектор-столбец x, обращающий все уравнения системы в тождества.
− искомым вектор-столбцом неизвестных системы. Решением СЛАУ является всякий вектор-столбец x, обращающий все уравнения системы в тождества.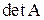 основной матрицы СЛАУ
основной матрицы СЛАУ 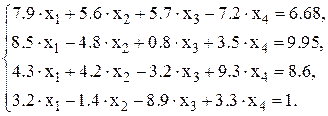
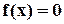 , где
, где 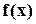 - некоторая нелинейная функция. Корнем или решением уравнения называется всякое значение
- некоторая нелинейная функция. Корнем или решением уравнения называется всякое значение  , обращающее уравнение в тождество, т. е.
, обращающее уравнение в тождество, т. е.  . В дальнейшем ограничимся рассмотрением лишь нелинейных уравнений с изолированными корнями, т. е. случая, когда для каждого корня уравнения существует окрестность, не содержащая других корней этого уравнения.
. В дальнейшем ограничимся рассмотрением лишь нелинейных уравнений с изолированными корнями, т. е. случая, когда для каждого корня уравнения существует окрестность, не содержащая других корней этого уравнения.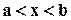 , называется алгебраической, если она имеет вид
, называется алгебраической, если она имеет вид 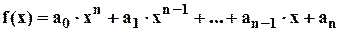 , где
, где 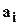 - некоторые действительные или комплексные числа. К трансцендентным уравнениям относятся неалгебраические нелинейные уравнения.
- некоторые действительные или комплексные числа. К трансцендентным уравнениям относятся неалгебраические нелинейные уравнения.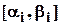 , в которых содержится один и только один корень уравнения
, в которых содержится один и только один корень уравнения  , i=1, 2, …;
, i=1, 2, …;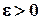 . Под этим может пониматься выполнение одного из двух условий:
. Под этим может пониматься выполнение одного из двух условий: 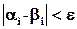
 или
или 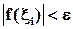 .
.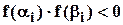 , то найдётся хотя бы одно число
, то найдётся хотя бы одно число  .
.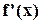 существует и сохраняет постоянный знак внутри интервала
существует и сохраняет постоянный знак внутри интервала  , т. е. если
, т. е. если 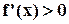 (или
(или 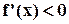 ) при
) при  .
. на отрезке [-10, +10].
на отрезке [-10, +10]. (Zoom In) и
(Zoom In) и  (Zoom Out), расположенные в графическом окне. В итоге получаем более удобное графическое представление (см. рис. 1.10,б), из которого следует, что корни уравнения находятся внутри отрезков [-3, -2], [0, 1] и [2, 3].
(Zoom Out), расположенные в графическом окне. В итоге получаем более удобное графическое представление (см. рис. 1.10,б), из которого следует, что корни уравнения находятся внутри отрезков [-3, -2], [0, 1] и [2, 3].