
|
|
Другим оператором ветвления является switch. У него следующий синтаксисswitch выражение case значение выражения1 операторы1 case {значение выражения2, значение выражения3, ...} операторы2. . . . . . . . . . . . . . . . . otherwise операторыNend Работает оператор switch следующим образом. 1. Находится значение выражения. 2. Если оно совпадает со значением выражения1, то выполняются опрераторы1. 3. Если оно совпадает с одним из результатов списка {значение выражения2, значение выражения3, ...}, то выполняются операторы2. 4. Если оно не совпадает ни с одним из значений выражений, то выполняется операторыN. Пример. Рассмотренный выше пример с использованием оператора switch будет иметь вид, показанный на рис. 2.5, а результат её вызова показан ниже
>> switchdemo(2) А равно двум или трём
Рис. 2.5. Окно редактора М-файла с функцией switchdemo(a)
Для конструирования условных выражений в MatLab используются следующие операции сравнения: == − равно, ~= − не равно, > − больше, < − меньше, >= − больше или равно, <= − меньше или равно. К логическим операциям относятся: A&B В MatLab установлен следующий приоритет (порядок выполнения) операций: 1. ~ (логическое НЕТ); 2. .’ (транспонирование), ^ (возведение в степень, в том числе поэлементно), унарный плюс и унарный минус; 3. * (умножение, в том числе поэлементное), / (деление, в том числе поэлементное); 4. + (сложение), - (вычитание); 5. == (равно), ~= (не равно), > (больше), < (меньше), >= (больше или равно), <= (меньше или равно); 6. A&B Для изменения порядка выполнения операций следует применять круглые скобки.
Циклические алгоритмы Для многократного выполнения некоторой последовательности операторов MatLab располагает двумя видами циклов: - for – его целесообразно использовать, если заранее известно число итераций в цикле; - while – его следует использовать, если цикл должен завершиться при выполнении некоторого условия и число итераций заранее не известно. Синтаксис оператора for следующий:
for count=start:step:final Операторы end
Здесь count − переменная цикла; start − её начальное значение; final − её конечное значение; шаг изменения переменной цикла. Цикл завершается как только count становится больше final. Значения параметров start, step и final могут быть как целыми так и вещественными. У оператора while следующий синтаксис:
while условие Операторы end
Если условие истинно, то выполняются операторы, в противном случае выполнение оператора while завершается. На рис. 2.6 представлено окно редактора М-файла с функцией count(x,n), результатом выполнения которой являются два числа F и W − значения суммы
вычисляемые с использованием циклов for и while соответственно. Результат вызова упомянутой функции показан ниже
>> [F W]=count(1,6) F = 23.5071 W = 23.5071
В MatLab имеются ещё два оператора, используемые вместе с рассмотренными операторами цикла. Первый из них (break) прерывает выполнение операторов цикла, а второй (continue) − влечёт за собой прекращение выполнения операторовтекущей итерации и переход на следующую (т.е или на проверку условия, если у нас оператор while, или на выполнение count=start:step:final − если у нас оператор for).
Рис. 2.6. Окно редактора М-файла с функцией count(x,n)
Разложение функций в ряд Фурье чрезвычайно широко используется в радиотехнике. Периодическая с периодом
Коэффициенты тригонометрического ряда Фурье вычисляют по формулам Эйлера-Фурье:
Справедливо следующее утверждение. Если функция f(x) кусочно-гладкая на отрезке
называется n-ой частичной суммой ряда Фурье. При этом Пример. Построим графики
Справа от графика функции f(x) записано её аналитическое выражение. Порядок выполнения задания следующий: 1. Формируем М-файл функцию fz(x) − см. рис. 2.7.
Рис. 2.7. Окно редактора М-файла с функцией fz(x)
2. Формируем две М-файл функции a(k) и b(k), вычисляющие соответственно значения коэффициентов
Рис. 2.8. Окно редактора М-файла с функциями a(k) и b(k)
2. Определяем функцию f(x). Для этого следует ввести клавиатуры символы f(x), нажать комбинацию клавиш <Shift>+<:>, затем следует щелкнуть по кнопке панели программирования. В открывшейся панели следует щелкнуть по кнопке Add Line , после чего, используя кнопки if этой же панели, кнопку |x| панели “калькулятор”, а также кнопки 3. 4. Определяем ak, bk и S(x,n). Здесь следует использовать панель “операций математического анализа”, а для ввода в рабочий документ, например, выражения ak:= следует нажать клавиши: a[k и комбинацию клавиш <Shift>+<:>. 5. В заключении строим график функции S(x,n), что также было рассмотрено ранее. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 and(A,B) − логическое И, A|B
and(A,B) − логическое И, A|B  ,
,
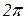 на отрезке
на отрезке  функция
функция  , где n − любое целое число, называется абсолютно интегрируемой на отрезке
, где n − любое целое число, называется абсолютно интегрируемой на отрезке  , если существует интеграл
, если существует интеграл  . Каждой абсолютно интегрируемой на отрезке
. Каждой абсолютно интегрируемой на отрезке 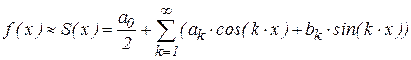 .
. .
.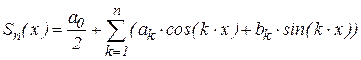
 , если f(x) непрерывна в точке
, если f(x) непрерывна в точке 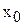 и
и  , если f(x) терпит разрыв первого рода (скачок) в точке
, если f(x) терпит разрыв первого рода (скачок) в точке  при n=12 для периодической с периодом
при n=12 для периодической с периодом  функции f(x), заданной следующим графиком на
функции f(x), заданной следующим графиком на 
 f(x)
f(x)




 0
0 -
-  -
- 
 и
и 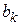 − см. рис. 2.8.
− см. рис. 2.8.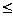 и > панели равенств и отношений строится определение функции f(x).
и > панели равенств и отношений строится определение функции f(x).



 Задаем диапазон изменения k (аналогично тому, как это делалось выше при построении таблицы функции).
Задаем диапазон изменения k (аналогично тому, как это делалось выше при построении таблицы функции).