|
|
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ1. Вычислить в соответствии с номером варианта выражение. Вычисления выполнить с использованием условного оператора и обоих операторов цикла. По результатам вычислений построить два графика на одной координатной плоскости. Процесс вычислений выполнить с использованием М-файл функций М-файл программы.
Аналитические выражения (не для печати)
2. Построить график частичной суммы ряда Фурье для заданного варианта функции f(x) при количестве слагаемых 5, 10 и 20. По результатам вычислений построить четыре графика на одной координатной плоскости и один график − на второй. Процесс вычислений выполнить с использованием М-файл функций и М-файл программы. Здесь при составлении подпрограммы вычисления функции следует применить, известное из аналитической геометрии уравнение прямой линии, проходящей через две заданные точки.
Варианты функции f(x) (не для печати)
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Поясните чем М-файл программа отличается от М-файл функции. 2. Запишите синтаксисы операторов if и switch. Объясните порядок их работы и особенности использования. 3. Запишите синтаксисы операторов for и while. Объясните порядок их работы и особенности использования. 4. Запишите установленный В MatLab приоритет операций. 5. Каковы сущность и порядок разложения функции в ряд Фурье?
Лабораторная работа № 3 Применение системы Matlab для исследования Электрических цепей
ЦЕЛЬ РАБОТЫ Ознакомление с особенностями использования системы MatLab для анализа нелинейных цепей, а также решения дифференциальных уравнений и системи получение первоначальных навыков её использования для анализа переходных процессов в электрических цепях.
3.1. ПОЯСНЕНИЯ К РАБОТЕ В радиотехнике решение нелинейных уравнений требуется, в частности, для анализа цепей, содержащих нелинейные элементы, например, полупроводниковые диоды, как в простейшем случае показано на рис. 3.1. Для приближения зависимости тока через диод как функции падения напряжения на нём
>> plot(x,f7(x)) >> grid on >> u=0.32; >> fzero('f7',u) ans = 0.3212
Рис. 3.1. Цепь, содержащая полупроводниковый диод
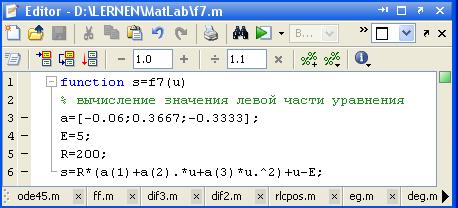
Рис. 3.2. Окно редактора М-файла с функцией
Рис. 3.3. Окно выходного графика
На рис. 3.5 не показан процесс определения коэффициентов степенного интерполяционного полинома, которые являются решением СЛАУ вида
где
Решение задачи Коши для дифференциальных уравнений и системы дифференциальных уравнений 1-го порядка. Если обыкновенное дифференциальное уравнение (ОДУ) 1-го порядка
Если обыкновенное дифференциальное уравнение (ОДУ) 2-го порядка
Численное решение нормальной системы дифференциальных уравнений 1-го порядка с системой начальных условий
состоит в построении таблицы приближенных значений В системе MatLab решение дифференциальных уравнений сводится к решению системы дифференциальных уравнений (пусть и состоящей из одного уравнения), поэтому вначале разберём порядок поиска решения для системы, а затем вернёмся к процедуре решения дифференциальных уравнений. Пример а. Найдем на отрезке [0, 3] приближенное решение задачи Коши для системы дифференциальных уравнений
и построим графики для найденного решения. На первом этапе построим специальную М-файл функцию для вычисления правых частей системы. Она должна иметь два входных аргумента: независимую переменную, по которой производится дифференцирование (в нашем случае, очевидно, ею является х − даже если х явно не входит в систему), и вектор искомых функций (в нашем случае, очевидно, вектор-столбец y с тремя элементами). Выходным аргументом М-файл функции является вектор правой части системы − как показано на рис. 3.4.
Рис. 3.4. Окно редактора М-файлов с функцией dif3
На втором этапе вызывается один из семи солверов (решателей) системы MatLab − мы ограничимся использованием лишь одного из них − ode45, который реализует рассмотренный выше одношаговый метод Рунге-Кутта четвёртого порядка. Он рекомендуется разработчиками MatLab в качестве первого для использования. Решение находится в виде таблица численных значений искомых функций До вызова солвера необходимо сформировать вектор-столбец начальных условий, например, как показано ниже
>> Y0=[1; 0; 1];
Синтаксис вызова солвера − один из трёх следующих: [X,Y]=ode45(‘fun’,[x0 xE],y0) [X,Y]=ode45(‘fun’,[x0:step:xE],y0) [X,Y]=ode45(‘fun’,[x0,x1,x2,…,xE],y0) , где Х − вектор-столбец значений независимой переменной с начальным значением х0 и конечным значением хЕ; step − шаг изменения этой независимой переменной; x0,x1,x2,…,xE − конкретная возрастающая или убывающая числовая последовательность, для которой необходимо найти искомое решение; fun − имя М-файла (в нашем случае dif3); y0 − имя вектора начальных условий. Пример
>> [T,Y]=ode45('dif3',[0:0.5:3],Y0) T = 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000 Y = 1.0000 0 1.0000 0.9324 0.4826 0.2211 0.5914 0.7973 -0.1700 0.0321 0.8621 -0.2202 -0.5190 0.9069 -0.0249 -0.8896 1.1735 0.2751 -1.1528 1.6915 0.5705
Значения искомых функций (в нашем случае это На последнем, третьем этапе, по значениям вектора-столбца X и столбцам матрицы Y можно, очевидно, построить графики (см. ниже).
>> plot(T,Y(:,1),'k-o',T,Y(:,2),'b-s',T,Y(:,3),'r-v') >> grid on
Рис. 3.5. Окно выходного графика
Пример b. Найдем на отрезке Вид М-файла с функцией dif1 представлен на рис. 3.6, график искомой функции − на рис. 3.7, а в командном окне необходимо, например, подать следующие команды
>> Y0=[1]; >> [T,Y]=ode45('dif1',[0:0.4:pi],Y0); >> plot(T,Y(:,1),'k-o') >> grid on
Рис. 3.6. Окно редактора М-файлов с функцией dif1
Рис. 3.7. Окно выходного графика
В радиотехнике ОДУ 1-го порядка применяются для анализа простейших электронных цепей во временной области, например, показанных на рис. 3.8. Там же приведены аналитические выражения, описывающие их. Искомыми при решении задачи анализа могут быть следующие параметры:
а) б) Рис. 3.8. Простейшие электронные цепи и описывающие их уравнения
Для составления дифференциальных уравнений, описывающих электронные цепи, используют законы Кирхгофа, известные из курса физики. При этом напряжения и токи на резисторе R, индуктивности L и ёмкости C, связаны соответственно следующими выражениями: Пример с. Для цепи рис. 3.8,а построить зависимости
>> Y0=[0]; >> [T,Y]=ode45('rl',[0:120e-6/100:120e-6],Y0); >> UR=5*Y; % напряжение на резисторе for t=0:120e-6/100:120e-6 if t<=5e-6 E=0; else E=1; end end >> UL=E-UR; % напряжение на индуктивности >> plot(T,Y(:,1),'k--',T,UR(:,1),'r-.',T,UL(:,1),'b-') >> grid on
Рис. 3.9. Окно редактора М-файлов с функцией rl
Рис. 3.10. Окно выходного графика
Для того, чтобы в системе MatLab решить задачу Коши для дифференциального уравнения n - ого порядка
с начальными условиями y(x0) = y0, y’(x0) = y1, …, y(n-1)(x0) = ynего приводят, как уже было сказано, к системе из n уравнений первого порядка и далее следуют описанной выше схеме из 3-х этапов. Пример d.Пусть требуется дифференциальное уравнение 2-го порядка вида
Для решения этой системы дифференциальных уравнений следует создать М-файл функцию, показанную на рис. 3.11 и в командном окне набрать следующий код (результат виден из рис. 3.12)
>> Y0=[0;1]; >> [T,Y]=ode45('dif2',[0:0.1:10],Y0); >> plot(T,Y(:,1),'k--',T,Y(:,2),'r-') >> grid on
Рис. 3.11. Окно редактора М-файла с функцией dif2
Рис. 3.12. Окно выходного графика
В радиотехнике ОДУ 2-го порядка применяются для анализа простых электронных цепей во временной области, например, показанных на рис. Х.10. Там же приведены аналитические выражения, описывающие их. Искомыми при решении задачи анализа могут быть следующие параметры:
а)
Рис. 3.13. Простые электронные цепи и описывающие их уравнения
Для составления дифференциальных уравнений, описывающих электронные цепи, используют законы Кирхгофа, известные из курса физики. При этом напряжения и токи на резисторе R, индуктивности L и ёмкости C, связаны соответственно следующими выражениями: Пример с. Для цепи рис. Х.10,а построить зависимости
>> Y0=[0;0]; >> [T,Y]=ode45('rlcpos',[0:0.1e-7:25e-6],Y0); plot(T,5*Y(:,1)) grid on
а)
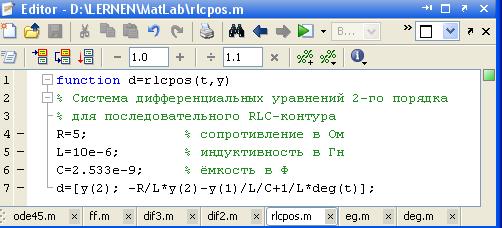
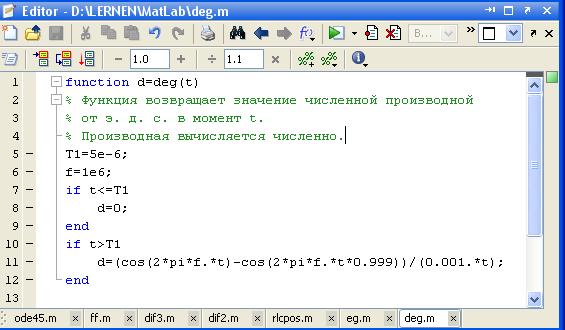
б) Рис. 3.14. Окна редакторов М-файлов с функциями
Рис. 3.15. Окно выходного графика

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


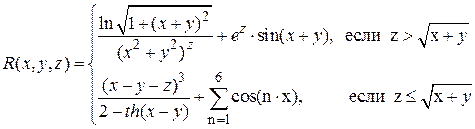
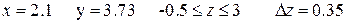
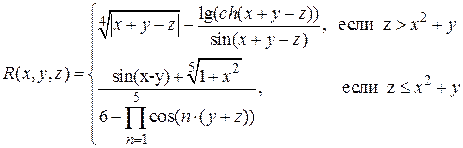

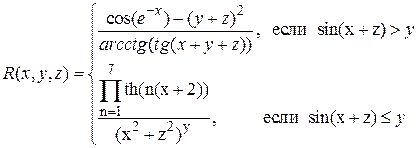


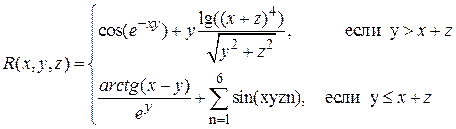

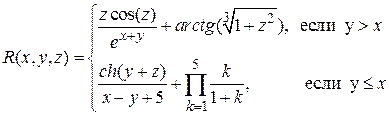



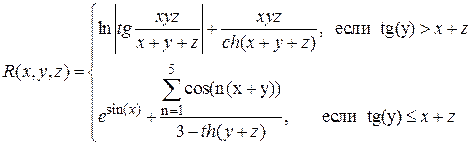





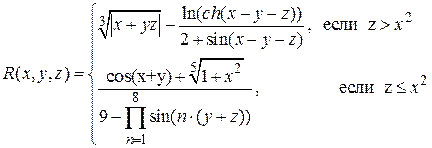





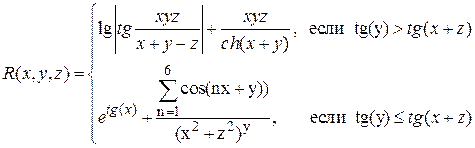










 -
-  -
- 




 -
- 






 1
1



 -1
-1






 -
- 





 -
- 









 -
- 








 -
- 






 чаще всего используют степенной
чаще всего используют степенной  или экспоненциальный
или экспоненциальный  полиномы невысокого порядка. Если эта зависимость определена, то процесс анализа нелинейной цепи с использованием пакета MatLabстановится достаточно простым, что показано ниже и на рис. 3.2, 3.3 (не показана процедура вычисления коэффициентов степенного интерполяционного полинома).
полиномы невысокого порядка. Если эта зависимость определена, то процесс анализа нелинейной цепи с использованием пакета MatLabстановится достаточно простым, что показано ниже и на рис. 3.2, 3.3 (не показана процедура вычисления коэффициентов степенного интерполяционного полинома).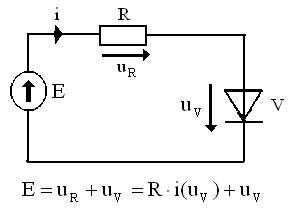

 ,
,
 − соответствующие друг другу векторы-столбцы отсчётов напряжения и тока, определяющих вольт-амперную характеристику диода. Для определения коэффициентов (А и
− соответствующие друг другу векторы-столбцы отсчётов напряжения и тока, определяющих вольт-амперную характеристику диода. Для определения коэффициентов (А и  ) экспоненциального полинома следует решить систему нелинейных уравнений вида
) экспоненциального полинома следует решить систему нелинейных уравнений вида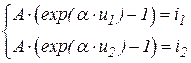 .
.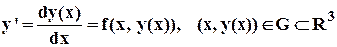 имеет в области G решение, то, вообще говоря, таких решений бесконечно много и они могут быть заданы в виде функций
имеет в области G решение, то, вообще говоря, таких решений бесконечно много и они могут быть заданы в виде функций  , где С - произвольная константа, такая, что
, где С - произвольная константа, такая, что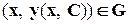 и
и 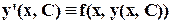 при произвольных значениях С. Если же необходимо найти решение, удовлетворяющее некоторому начальному условию y(x0) = y0, то говорят об отыскании решения задачи Коши.
при произвольных значениях С. Если же необходимо найти решение, удовлетворяющее некоторому начальному условию y(x0) = y0, то говорят об отыскании решения задачи Коши. имеет в области G решение, то, вообще говоря, таких решений бесконечно много и они могут быть заданы в виде функций
имеет в области G решение, то, вообще говоря, таких решений бесконечно много и они могут быть заданы в виде функций  при произвольных значениях С. Если же необходимо найти решение, удовлетворяющее некоторому начальному условиям y(x0) = y0, y’(x0) = y10то говорят об отыскании решения задачи Коши.
при произвольных значениях С. Если же необходимо найти решение, удовлетворяющее некоторому начальному условиям y(x0) = y0, y’(x0) = y10то говорят об отыскании решения задачи Коши.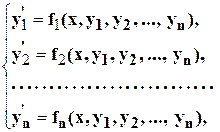


 I = 1, 2, ..., N, решения
I = 1, 2, ..., N, решения  на отрезке
на отрезке  с начальными условиями
с начальными условиями 

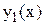 ,
, 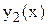 и
и 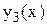 располагаются по столбцам.
располагаются по столбцам.
 приближенное решение ОДУ 1-го порядка y’ = sin(x.y), удовлетворяющее начальным условиям y(0) = 1, и построим график найденного решения. Шаг изменения независимой переменной х − 0.4.
приближенное решение ОДУ 1-го порядка y’ = sin(x.y), удовлетворяющее начальным условиям y(0) = 1, и построим график найденного решения. Шаг изменения независимой переменной х − 0.4.

 . Очевидно, что для решения задачи Коши необходимы также и начальные условия − для цепи рис. 3.8,а их обычно задают в виде
. Очевидно, что для решения задачи Коши необходимы также и начальные условия − для цепи рис. 3.8,а их обычно задают в виде 
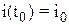 , а для цепи рис. 3.8,б −
, а для цепи рис. 3.8,б −  .
.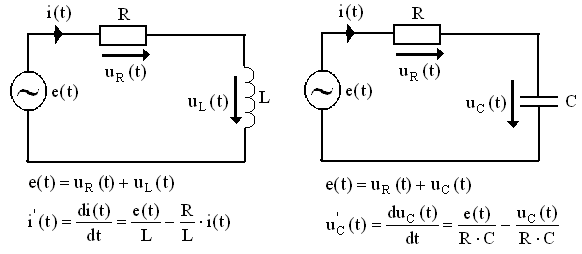
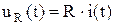 ,
, 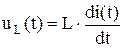 и
и  .
.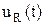 и
и  для диапазона времён
для диапазона времён  при
при  и э. д. с., в виде ступеньки напряжения
и э. д. с., в виде ступеньки напряжения  . Число узлов сетки выбрать равным 100. Очевидно, что при
. Число узлов сетки выбрать равным 100. Очевидно, что при  мы имеем
мы имеем  − это и будут наши начальные условия. Фрагмент соответствующего командного окна, решающего поставленную задачу, а также виды окна М-файла и итогового графического окна, представлен ниже и на рис. 3.9 и 3.10.
− это и будут наши начальные условия. Фрагмент соответствующего командного окна, решающего поставленную задачу, а также виды окна М-файла и итогового графического окна, представлен ниже и на рис. 3.9 и 3.10.
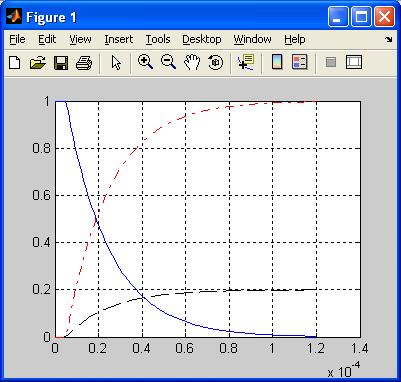

 , при начальных условиях y(0) = 1, y’(0) = 0 на отрезке [0, 10] с шагом 0.1. Для приведения дифференциального уравнения n-ого порядка к системе из n дифференциальных уравнений 1-го порядка вводят n вспомогательных функций. Для нашего случая это выглядит так: y1 = y, y2 = y’. После этого дифференциальное уравнение можно заменить на систему
, при начальных условиях y(0) = 1, y’(0) = 0 на отрезке [0, 10] с шагом 0.1. Для приведения дифференциального уравнения n-ого порядка к системе из n дифференциальных уравнений 1-го порядка вводят n вспомогательных функций. Для нашего случая это выглядит так: y1 = y, y2 = y’. После этого дифференциальное уравнение можно заменить на систему при начальных условиях
при начальных условиях  .
.

 , а для цепи рис. 3.13,б −
, а для цепи рис. 3.13,б −  ,
,  .
.
 б)
б)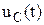 в диапазоне времён
в диапазоне времён  при
при 
 и э. д. с., в виде ступеньки гармонического колебания
и э. д. с., в виде ступеньки гармонического колебания 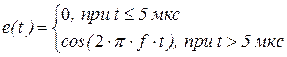 , где
, где  . Шаг сетки времени выбрать равным 10 нсек. Очевидно, что при
. Шаг сетки времени выбрать равным 10 нсек. Очевидно, что при 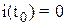 ,
,  − это и будут наши начальные условия. Фрагмент соответствующего командного окна, решающего поставленную задачу, а также виды окон М-файлов и итогового графического окна, представлен ниже и на рис. 3.14 и 3.15.
− это и будут наши начальные условия. Фрагмент соответствующего командного окна, решающего поставленную задачу, а также виды окон М-файлов и итогового графического окна, представлен ниже и на рис. 3.14 и 3.15.