|
|
В задачах 1 - 20 найти общее решение дифференциального уравнения.1. 3. 5. 7. 9. 11. 13. 15. 17. 19.
В задачах 21-40 найти решение задачи Коши.
В задачах 41 – 60 найти общее решение дифференциального уравнения. 41. 43. 45. 47. 49. 51. 53. 55. 57. 59.
В задачах 61 - 80 найти общее решение дифференциального уравнения.
Примеры выполнения тестовых заданий Интернет - экзамена
В настоящее время тестовые методы контроля знаний получили очень широкое распространение. Федеральный интернет-экзамен является одной из общегосударственной форм тестирования. В нем участвует большинство Высших учебных заведений (ВУЗов) России. Результаты этого экзамена являются одним из показателей работы ВУЗа. Целью Федерального интернет-экзамена является оценка степени соответствия содержания и уровня подготовки студентов требованиям Государственного образовательного стандарта (ГОС) Высшего профессионального образования (ВПО). Правила тестирования
Указания: На экране монитора перед каждым ответом из предложенного набора стоит один из знаков: Знак Необходимо отметь щелчком левой клавиши «мышки» знак Знак Сначала, необходимо найти и отметить щелчком левой клавиши «мышки» знак В выбранном квадратике появляется цифра 1. Затем надо отметить квадратик, соответствующий второму варианту ответа – появляется цифра 2 и т.д.
Знак - предполагает введение ответа в рамку.
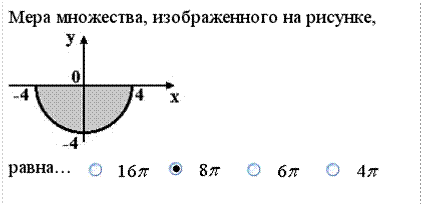
Функции. Множества. Свойства функций Задание 1.
Решение: Мерами закрытых геометрических множеств являются: длина отрезка, площадь плоской фигуры и объем тела. Понятие меры распространяется и на соответствующие полузакрытые и открытые геометрические множества. В данном случае задано закрытое плоское множество (полуокружность). Его мерой является площадь. Задание 2.
Найдем множество значений переменной x, удовлетворяющих неравенству
Значит Множество Множество Множество
Задание 3.
Решение. Окрестностью точки
Задание 4.
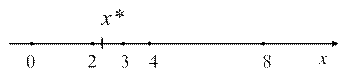
Решение. Найдем сначала приближенное значение корня уравнения, принадлежащее отрезку
По оси ох видно, что Метод половинного деления является одним из итерационных методов приближенного решения алгебраических уравнений. За начальное приближение к искомому корню можно взять одну из границ отрезка локализации корня. Пусть
В данном задании мы знаем приближенное значение корня и соответственно сужаем отрезок локализации (см. рис.): Далее по аналогии:
Итак: Задание 5.
Пояснения. Гармонические колебания определяются одной из периодических функций:
где А – амплитуда колебаний, ω – частота колебаний, φ – начальная фаза колебаний. Задание 6.
Пояснения. Функция В данном случае из графиков видно, что периодически повторяемой является только одна функция. Ее наименьший период: Задание 7.
Решение. Найдем область определения функции (ООФ).
Значит данная, функция имеет только один разрыв (в точке Задание 8.
Решение. ООФ: Воспользуемся методом интервалов:
Таким образом,
Производные функций одной и нескольких переменных Задание 1.
Решение. Воспользуемся формулой
Задание 2.
Решение. Воспользуемся формулой В данном случае Задание 3.
Решение. Воспользуемся формулой для производной произведения двух функций:
Задание 4.
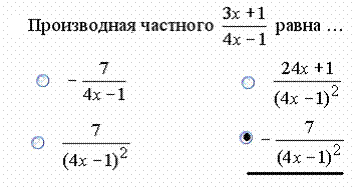
Решение. Воспользуемся формулой для производной частного:
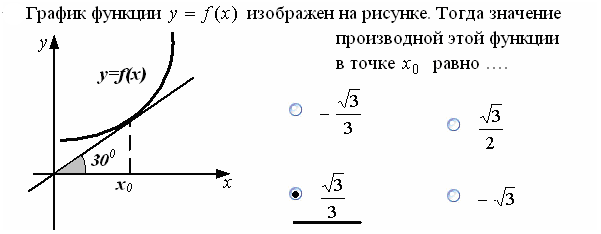
Задание 5.
Решение. Производная функции в точке касания равна тангенсу угла наклона касательной к положительному направлению оси Ох.
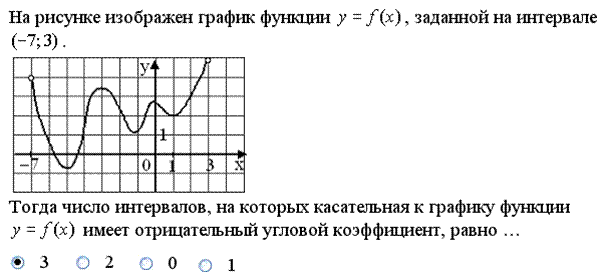
Задание 6.
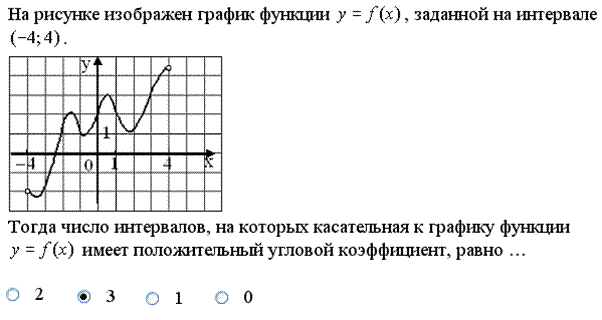
Пояснения. Уравнение касательной к графику функции
Угловой коэффициент прямой определяется формулой В данном случае надо установить число интервалов, на которых производная отрицательна, т.е. функция убывает. Из графика видно, что таких интервалов 3. Задание 7.
Пояснения. Для касательной Задание 8.
Решение. Градиентом функции где Напомним, что при отыскании частных производных используются все те же формулы и правила, что и при отыскании производных функций одной переменной. Однако при дифференцировании по одной из переменных все остальные независимые переменные считаются постоянными, например, при дифференцировании по переменной х переменные В данном случае:
Тогда в точке М(3; -1; 4):
Задание 9.
Решение.
В данном случае:
Тогда в точке М(1; -2; 3): Задание 10.
Решение. Тригонометрическая форма комплексного числа В данном случае по геометрической иллюстрации видно, что Задание 11.
Решение. При дифференцировании функций комплексной переменной В данном случае:
Тогда

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 2.
2. 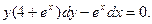
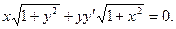 4.
4. 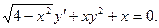
 6.
6. 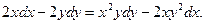
 8.
8. 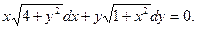
 10.
10. 
 12.
12. 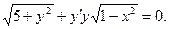
 14.
14. 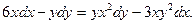
 16.
16. 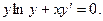
 18.
18. 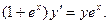
 20.
20. 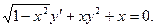
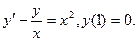




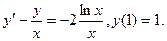



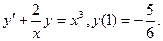

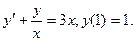



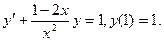


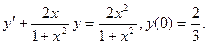

 42.
42. 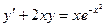
 44.
44. 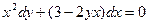
 46.
46. 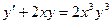
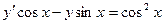 48.
48. 
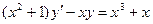 50.
50. 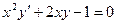
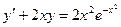 52.
52. 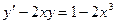
 54.
54. 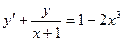
 56.
56. 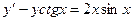
 58.
58. 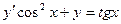
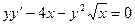 60.
60. 


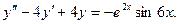




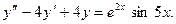

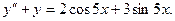
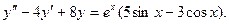
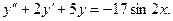







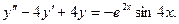

 или
или  .
. Знак
Знак  - предполагает указание одного, двух или более ответов.
- предполагает указание одного, двух или более ответов.
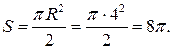
 Решение.
Решение. т.е. решим это неравенство. Воспользуемся методом интервалов.
т.е. решим это неравенство. Воспользуемся методом интервалов.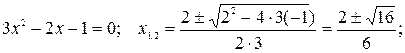
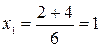 ;
; 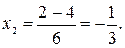
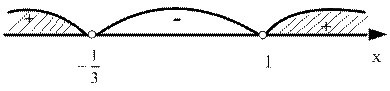

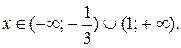
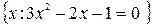 составляют только две точки
составляют только две точки  и
и  , т.е.
, т.е. 
 определяется интервалом
определяется интервалом 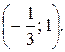
 определяется отрезком
определяется отрезком 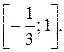


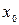 является симметричный интервал, включающий эту точку:
является симметричный интервал, включающий эту точку:  В данном случае
В данном случае  =0,2
=0,2  (8,3; 8,7).
(8,3; 8,7).

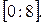

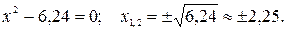
 .
.
 .
.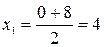 .
. .
.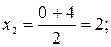
 ;
; 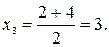
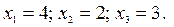


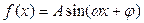 или
или 
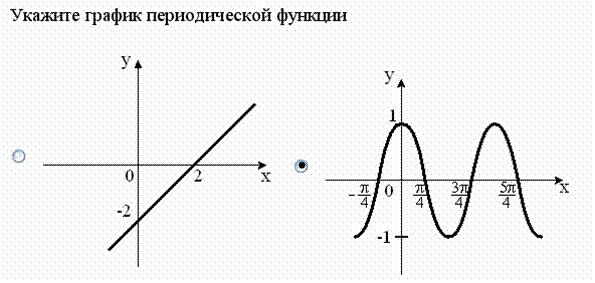
 ,
,
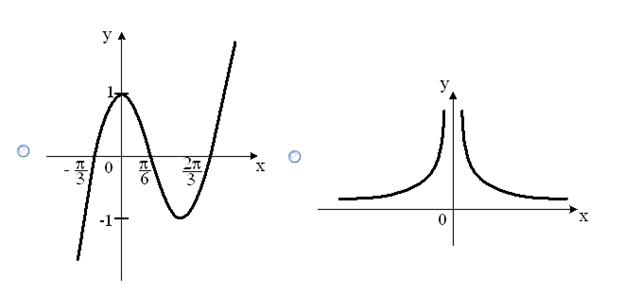
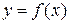 является периодической на множестве Е, если на этом множестве выполняется условие
является периодической на множестве Е, если на этом множестве выполняется условие  , где Т число, называемое периодом этой функции. Например, периодическими являются функции
, где Т число, называемое периодом этой функции. Например, периодическими являются функции  , для этих функций наименьший период
, для этих функций наименьший период  .
. . Очевидно, что уравнение этой функции имеет вид
. Очевидно, что уравнение этой функции имеет вид  .
.

 или
или  , т.е.
, т.е.  .
. ).
).
 ;
;  .
.
 .
.

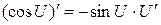 . В данном случае
. В данном случае 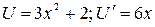 .
. 

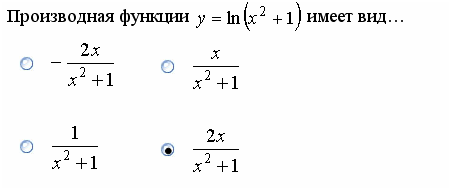
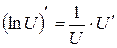 .
.
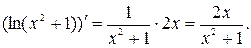

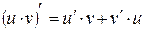 .
.
 :
: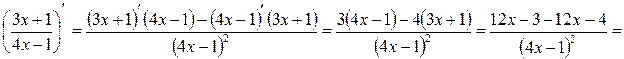
 .
.
 .
.
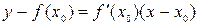 , где
, где  - точка касания.
- точка касания.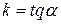 , где α – угол между прямой и осью ох. Для касательной
, где α – угол между прямой и осью ох. Для касательной 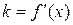 .
.

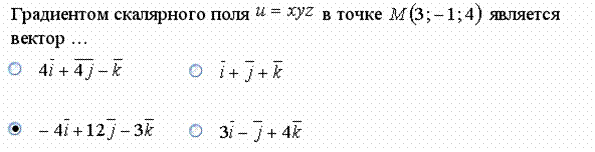
 или градиентом скалярного поля
или градиентом скалярного поля  называется вектор
называется вектор 
 - единичные векторы (орты), направленные по осям координат,
- единичные векторы (орты), направленные по осям координат,  - частные производные функции
- частные производные функции 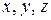 соответственно.
соответственно. считаются постоянными.
считаются постоянными.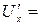
 ;
; 
 ;
;
 .
. 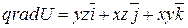 .
.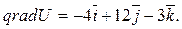

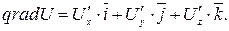
 ;
;  ;
;  ;
;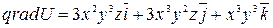 .
.

 имеет вид:
имеет вид:  , где
, где 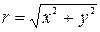 ;
;  .
.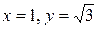 и
и  . Значит
. Значит  и
и 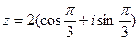 .
.
 используются формулы и правила дифференцирования функций одной действительной переменной.
используются формулы и правила дифференцирования функций одной действительной переменной. ;
; 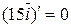 , как производная от комплексного числа
, как производная от комплексного числа  .
.  ;
;