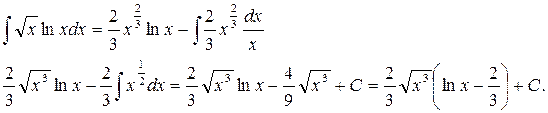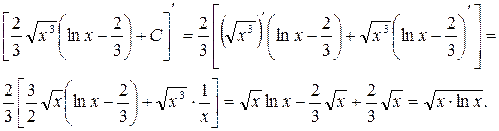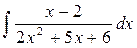|
|
Исследовать функцию и построить ее график1.
4.
7.
10.
13.
16.
19.
Решить оптимизационные задачи:
1. Требуется изготовить цилиндрический сосуд заданного объема V, открытый сверху. Определить его радиус и высоту, чтобы поверхность сосуда была наименьшей. 2. Какие размеры должен иметь цилиндр, поверхность которого равна S, чтобы его объем был наибольшим? 3. Окно имеет форму прямоугольника, завершенного полукругом. Определить размеры окна, при заданном периметре имеющего наибольшую площадь. 4. Боковая сторона равнобочной трапеции конгруэнтна ее меньшему основанию и имеет длину, равную 9 см. Какова должна быть длина большего основания, чтобы площадь трапеции была наибольшей? 5. Из круглого бревна диаметра D вырезать балку прямоугольного сечения, чтобы площадь сечения была наибольшей. 6. В данный шар радиуса R вписать цилиндр наибольшего объема. 7. Одна сторона прямоугольного участка земли примыкает к берегу канала, а три другие огораживаются забором. Каковы должны быть размеры этого участка, чтобы его площадь равнялась 800 м2 , а длина забора была наименьшая? 8. В прямоугольном листе картона длиной 48 см и шириной 30 см вырезаются по углам одинаковые квадраты и из оставшейся части склеивается открытая прямоугольная коробка. Какова должна быть сторона вырезаемых квадратов, чтобы объем коробки был наибольшим? 9. Тело представляет собой круговой цилиндр, завершенный сверху полушаром. При каких линейных размерах это тело будет иметь наименьшую полную поверхность, если объем его равен V? 10. На странице книги печатный текст должен занимать (вместе с промежутками между строками) 192 см2 . Верхнее и нижнее поля должны быть по 4 см, правое и левое поля – по 3 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы? Дифференцирование функций нескольких переменных Литература: [1] гл.15, §1-5, 8-11; [2] гл.12, §1-4, 6-8; [3] гл.9, §43-44,46; [4] гл.11, §1-6, 12; [5] гл.8, §1-2,12. Разберите решение заданий 16,17 Задание 16. Найти: а) частные производные первого порядка z= б) частные производные сложных функций в) частные производные второго порядка Решение. а) Находим частную производную
Находим частную производную
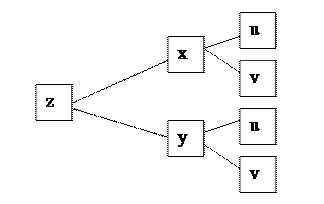
б) частные производные сложной функции z=x2lny, где х =
тогда
Находим частные производные данных функций:
По формуле (1) находим:
По формуле (2) находим:
в)z=ln(x2+y2). Находим первые производные:
Дифференцируя каждое из полученных частных производных по х и по у получим вторые частные производные:
= 2x. (-1)(x2+y2)-2.2y = -
= 2y. (-1)(x2+y2)-2.2x = -
Смешанные частные производные Задание 17. Исследовать на экстремум функцию z=2x3+2y3-36xy+430. Решение. Определение экстремума функции двух независимых переменных следует выполнять в следующей последовательности. 1. Найти частные производные 1-го порядка. 2. Определить стационарные точки, в которых функция может достигать экстремума, для чего необходимо решить систему уравнений: 3.
Определить частные производные 2-го порядка 4.
Вычислить значения частных производных 2-го порядка в каждой стационарной точке, а полученные числа обозначить через А,В,С. 5.
Составить определитель При этом: а) если D>0 , то экстремум в стационарной точке есть: если А>0, то будет минимум, при А<0 – максимум; б) если D<0, то экстремума в рассматриваемой точке нет; в) если D=0, то имеет место сомнительный случай, требуется дополнительное исследование. 1). Находим частные производные 1-го порядка
2). Найдем стационарные точки, решая систему уравнений С помощью подстановки у=х2/6 получим х4/36-6х=0 или х4-216х=0. Решим уравнение. Перепишем его в виде х(х3-216)=0. Разложим на множители х(х-6)(х2+6х+36)=0. Следовательно х1=0; х2=6; остальные два корня комплексные (корни уравнения х2+6х+36=0). Подставляя значения х1 и х2 в уравнение у=х2/6, получим у1=0; у2=6. Получим две стационарные точки М1(0;0) и М2(6;6). Проверим эти точки на экстремум с помощью достаточных условий. Для этого:
3). Найдем частные производные второго порядка 4). Подставляя координаты стационарных точек, получим а) для точки М1 А=(¶2z/¶x2)x=0 = 0; B=(¶2z/¶x¶y)x=0 = -36; C=(¶2z/¶y2)x=0 = 0 y=0 y=0 y=0 5). Вычислим D=А.С-В2=0-(-36)2=-1296<0. Так как D<0, то при х=0 и у=0 функция не имеет экстремума. б) для точки М2 А=(¶2z/¶x2)x=6 = 12.6=72; B=(¶2z/¶x¶y)x=6 = -36; C=(¶2z/¶y2)x=6 = 12.6=72. у=6 y=6 y=6 Тогда D=А.С-В2=72.72-(-36)2= 3888>0. Так как D>0, то при х=6 и у=6 данная функция имеет экстремум. Поскольку А>0 (или С>0), то точка М2 является точкой минимума. Значение функции в этой точке z min=z(6;6)=2.63+2.63-36.6.6+430= - 432+430= -2. Вопросы для самопроверки
1. Дайте определение функции двух независимых переменных. Приведите примеры. 2. Что называется областью определения функции двух независимых переменных? Каково геометрическое изображение функции двух переменных. 3. Дайте определение частного и полного приращения функции двух независимых переменных. 4. Сформулируйте определение предела функции двух переменных. 5. Какая функция называется непрерывной в точке? в области? 6. Дайте определение частных производных первого порядка функции двух переменных. Каков их геометрический смысл ? 7. Что называется полным дифференциалом функции двух переменных? 8. Как найти частные производные второго порядка функции двух переменных? 9. Сформулируйте необходимое условие экстремума функции двух 10. Сформулируйте достаточный признак экстремума функции двух переменных.
Задания для самостоятельного решения а) частные производные первого порядка б) частные производные сложных функций в) частные производные второго порядка
1. a) z=lnSin(x-2y) б) z=arcSin(x-y); x=uv; y= в) z= 2. a) z= б) z=ln(х2-у2); x=uv; y= в) z=
3. a) z=ух4Соs2y б) z=arctg в) z=
4. a) z= б) z=x2y-y2x; x=uCosv; y=uSinv в) z=arctg 5. a) z=ln(x+ б) z= в) z=x2Sin 6. a) z=arctg б) z=х2+y3; x=u2-v2; y=e в) z=exCosy 7. a) z=e б) z=х3+y3; x=ln в) z=Cos(x+ey ) 8. a) z=x2ln(x2+y2) б) z= ln(x-y2); x=u2+v2; y=vu в) z=e 9. a) z=arcSin(x+ey) б) z=ln в) z=ln(y+ 10. a) z=Sinylnx+exlny б) z= в) z=ln(x2-y2)
В задачах11-30 исследовать функцию двух переменных z=f(x;y) 11. z = x3 + y3 – 9xy + 27 12. z = y3 + 15x2 – 30xy + 9y2 + 60x – 51y + 5 13. z = 6y2 – y3 + 3x2 - 6xy – 6x – 6y – 3 14. z = 2y3 + 3x2 – 12xy + 18y2 – 18x + 36y - 1 15. z = 2y3 + 3x2 – 12xy +15y2 + 12y - 6x – 7 16. z = 2y3 – 6x2 + 24xy – 21y2 – 12x + 12y + 3 17. z = 2x3 + 12x2 – 6xy + 3y2 + 6x + 6y - 1 18. z = 2x3 – 24x2 + 12xy – 3y2 – 30x + 5 19. z = x3 – 12x2 + 12xy – 3y2 – 6y – 1 20. z = x3 – 15x2 + 12xy – 3y2 + 12x – 6y – 1 21. z = -2x3 – 12x2 + 12xy – 3y2 + 54x + 3 22. z = 2y3 – 3x2 + 12xy – 15y2 – 6x + 12y – 1 23. z = 4x3 + 24x2 + 36xy + 9y2 – 108x + 36y – 1 24. z= 2x3 – 24x2 + 18xy – 9y2 – 36y – 3 25. z = 2y3 + 3x2 + 6xy – 6y2 – 6x + 6y – 1 26. z = 2x3 + 18x2 – 12xy + 3y2 + 36x – 18y – 1 27. z = 2y3 – 6x2 + 18xy – 6y2 – 12y + 5 28. z = 2y3 + 3x2 + 6xy – 6y2 – 12x + 3 29. z = 9x2 + 2x3 – 12xy + 16y2 – 12y – 1 30. z = -4y3 + 9x2 – 36xy + 24y2 – 36x + 108y – 1
Неопределенный интеграл
Литература: [1] гл.13, §1-8; [2] гл.7, §1-5; [3] гл.7, §29-32; [4] гл.8, §1-7; [5] гл.9, §1-4.Разберите решение заданий 17-21. Задание 17. Вычислить интеграл
Решение. Преобразуем подынтегральную функцию:
Далее представляем интеграл алгебраической суммы в виде суммы интегралов слагаемых, вынося постоянные множители за знаки интегралов, и, пользуясь таблицей интегралов, получим:
Проверка:
Задание 18.Вычислить интеграл Решение. Первый способ. Полагая
Второй способ. Умножая и деля на –2 и замечая, что
Проверка:
Задание 19.Вычислить интеграл Решение. Для вычисления интеграла от функции, содержащей квадратный трехчлен, надо выделить полный квадрат их квадратного трехчлена, заменить переменную, в результате чего получим табличные интегралы. Выделяя полный квадрат в знаменателе, имеем:
Проверка:
Задание 20. Вычислить интеграл Решение. При вычислении этого интеграла надо применить метод интегрирования по частям. Положив
Подставляя в формулу
Проверка:
При интегрировании по частям важен выбор функции u и v. В качестве u выбирается та часть подынтегрального выражения, которая существенно упрощается при дифференцировании. За dv – та часть подынтегрального выражения вместе с dx, которая может быть проинтегрирована.
Задание 21. Найти неопределенный интеграл Решение.
Преобразуем дробь, стоящую под интегралом. Выделим в числителе из (х-2), производную знаменателя, равную (2х2+5х+6)¢=4х+5. Чтобы величина числителя не изменилась, запишем
Поэтому
После выделения в числителе производной знаменателя преобразуем интеграл в разность двух интегралов. Во втором интеграле в знаменателе выделяем полный квадрат. Вопросы для самопроверки
1. Сформулируйте определение первообразной функции. 2. Что называется неопределенным интегралом от данной функции? 3. Перечислите основные свойства неопределенного интеграла. 4. Напишите формулы основных интегралов. 5. В чем сущность метода интегрирования заменой переменной? 6. Напишите формулу интегрирования по частям в неопределенном интеграле. Задания для самостоятельного решения В задачах 1-20 найти неопределенные интегралы и результаты интегрирования проверить дифференцированием.
2.6.
Определенный интеграл
Литература: [1] ч.1, гл.14, §1-8,12; [2] гл.8, §1-4, 7-12; [3] гл.8, §35-41. [4] гл.9, §1-5; [5] гл.10, §1-6.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 2.
2.  3.
3. 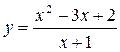
 5.
5.  6.
6. 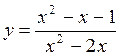
 8.
8.  9.
9. 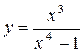
 11.
11.  12.
12. 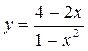
 14.
14.  15.
15. 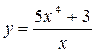
 17.
17.  18.
18. 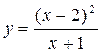
 20.
20. 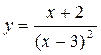
 ,
,  для функции:
для функции: .
. ,
,  для функции z=x2lny, где х =
для функции z=x2lny, где х = 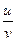 , у =
, у = 
 ,
,  ,
,  ,
,  для функции z=ln(x2+y2). Убедиться, что
для функции z=ln(x2+y2). Убедиться, что  =
=  =
=  = =
= =  =
=  = =
= =  .
. =
=  =
=  =
= =
=  =
=  .
.

 =
=  +
+ 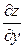 .
.  (1)
(1) =
=  +
+  (2)
(2) = 2xlny;
= 2xlny;  = (х2lny)
= (х2lny)  =
= 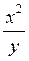
 =
=  =
=  ;
;  =
=  = u(v-1)
= u(v-1)  = -
= - 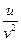
 = (uv)
= (uv)  = v;
= v; 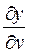 = (uv)
= (uv)  = u
= u = 2
= 2  =
= 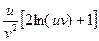
 = -2
= -2 
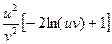
 =
= 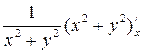 =
= 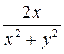 .
.  =
=  =
=  .
. =
=  =
= 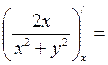

 = =
= =  ;
;
 =
=  2х((х2+у2) -1)
2х((х2+у2) -1)  =
= ;
;
 =
=  2y((х2+у2) -1)
2y((х2+у2) -1)  =
=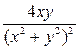 ;
;
 =
= 

 = =
= =  .
. и
и  равны.
равны.

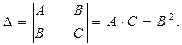



 переменных.
переменных.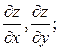

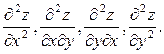
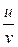
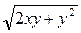
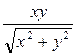
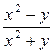
 ; x=uSinv; y=uCosv
; x=uSinv; y=uCosv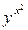
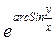

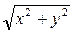 )
) ; x=vlnu; y=ulnv
; x=vlnu; y=ulnv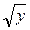

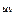
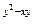
 ; y=arctg
; y=arctg 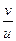
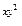
 ; x=Sin
; x=Sin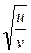
 ; x=ln(u2+v2); y=uv2
; x=ln(u2+v2); y=uv2 .
. .
.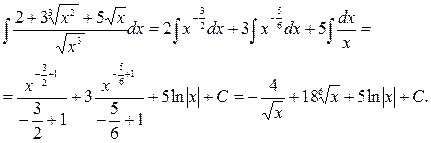
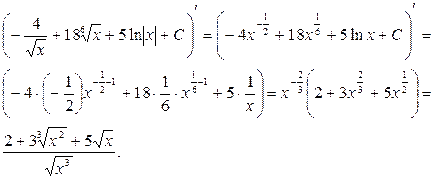
 .
. , получим
, получим .
. .
. , получим
, получим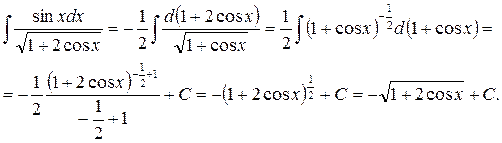
 .
.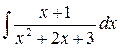 .
. . Далее, заменяя
. Далее, заменяя  ,
,  , получим:
, получим: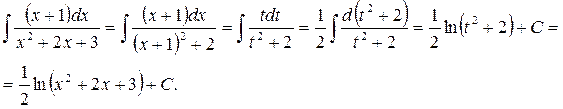
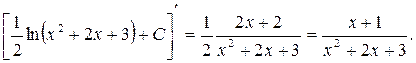
 .
. ,
,  , найдем:
, найдем:
 .
. , получим
, получим