
|
|
В задачах 1 - 20 вычислить двойные интегралы. Сделать чертеж.
7. a) б)
8. a) б)
9. a) б)
10. a) б)
11. a) б)
12. a) б)
13. a) б)
14. a) б)
15. a) б)
16. a) б)
17. a) б)
18. a) б)
19. a) б)
20. a) б)
В задачах 21 – 40 найти площадь области Д, ограниченную линиями:
31. y = 0; y = 4; y = - x; y = 32. y = 33. y = x2; x + y = 6 34. y2 = 2x; y= - x 35. y = 4x - x2; y = 3x2 36. y2 = - x + 4; y2 = 2x - 5 37. y = 38. y = 39. y = lnx; y = x – 1; y = - 1 40. y2 = - x; x = - 4
Дифференциальные уравнения
Литература: [1] гл.22, §1-5, 7-9, 11-13; [2] гл.15, §1-4; [3] ч.2, гл.1, §1-6; [4] гл.12, §1-5, 7-9; [5] ч.2, гл.4, §1-3. Разберите решения заданий 34 - 38. Задание 34. Найти общее решение дифференциального уравнения
Решение.Учитывая, что
Умножим на dx правую и левую части равенства
Полученное уравнение является дифференциальным уравнением с разделяющимися переменными. Разделим переменные, деля обе части равенства на произведение “лишних” членов
После сокращения, получим
Проинтегрируем обе части равенства
После интегрирования получим
Запишем общее решение дифференциального уравнения (1)
Решение дифференциального уравнения может быть записано также относительно х. Для этого перепишем уравнение (1) в следующем виде
В данном случае неопределенная константа С представлена в виде lnC. Преобразуем
Потенцируем полученное равенство: Получаем решение дифференциального уравнения
Заменив 1/C=C1, получим
Общеерешение дифференциального уравнения может быть представлено также относительно С в виде  . .
Задание 35. Найти частное решение дифференциального уравнения удовлетворяющее начальному условию:
Решение. Данное уравнение является уравнением с разделяющимися переменными. Делим обе части уравнения на
Интегрируем обе части уравнения
Интеграл, стоящий в правой части уравнения, найдем, применив замену переменной
Запишем общее решение дифференциального уравнения
Подставляя начальные условия в общее решение, найдем произвольную постоянную С.
Найденное значение С=-2 подставляем в общее решение и получаем частное решение
Задание 36. Найти общее решение дифференциального уравнения
Решение. Приведем данное уравнение к виду
Проверим, является ли 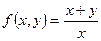 однородной функцией. однородной функцией.
Получили Введем подстановку
Отсюда
Проинтегрируем его
Получим решение уравнения  . .
Заменяя
Окончательно находим общее решение дифференциального уравнения
Задание 37. Найти общее решение дифференциального уравнения
Уравнение вида Решение. Данное уравнение линейное.
Находим решение уравнения в виде произведения двух функций
и данное уравнение примет вид
 . .
Подбираем v таким образом, чтобы
или
Заменив в последнем уравнении
Решим уравнение
Интегрируя это уравнение
получим
Потенцируя последнее уравнение получим
Оставшаяся часть уравнения имеет вид
Подставив в это уравнение
Производя сокращение на (х+1)2 и умножение на dx правой и левой части равенства, получим
Решим уравнение (проинтегрируем)
Найдем интеграл в правой части уравнения
Решение второй части уравнения
Общее решение данного уравнения
Задание 38. Найти общее решение дифференциального уравнения
Решение.Данное уравнение - неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами, общий вид которого Для отыскания общего решения уравнения (1) сначала нужно найти общее решение Y уравнения (2), затем найти какое-либо частное решение
Для отыскания частного решения наиболее часто применяют метод неопределенных коэффициентов. Пусть
где
где Вначале находим решение соответствующего однородного уравнения: Для этого составляем характеристическое уравнение и находим его корни:
Характеристическое уравнение имеет действительный кратный корень. В соответствии с формулой Определяем вид частного решения исходного уравнения по виду правой части:
где Так как число Находим производные функции
Для нахождения коэффициентов А и В подставим выражения
Приведем подобные члены и получим:
Приравнивая коэффициенты при
решением которой являются числа
Следовательно, частное решение определяется формулой
На основании формулы
Вопросы для самопроверки
1. Что называется дифференциальным уравнением? 2. Что называется общим решением дифференциального уравнения? частным решением? 3. Каков геометрический смысл частного решения дифференциального уравнения первого порядка? 4. Приведите примеры дифференциальных уравнений с разделяющимися переменными. 5. Какое дифференциальное уравнение первого порядка называется линейным? уравнением Бернулли? Укажите способ его решения. 6. Какое уравнение называется линейным дифференциальным уравнением второго порядка? 7. Какое уравнение называется характеристическим для однородного дифференциального уравнения второго порядка? 8. Какой вид имеет общее решение однородного дифференциального уравнения второго порядка в зависимости от дискриминанта характеристического уравнения? 9. Как найти общее решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами? 10. Какой вид имеет частное решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами, если его правая часть есть многочлен? показательная функция? тригонометрическая функция?
Задания для самостоятельного решения 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|



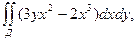




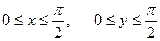





 x = 2
x = 2



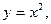


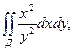
 x = 2
x = 2
 если Д:
если Д: 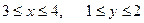
 где Д ограничена линиями
где Д ограничена линиями 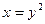
 если Д:
если Д: 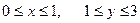
 где Д ограничена линиями
где Д ограничена линиями 
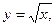
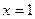
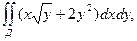 если Д:
если Д: 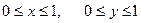
 где Д ограничена линиями
где Д ограничена линиями 


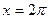
 если Д:
если Д: 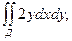 где Д ограничена линиями
где Д ограничена линиями 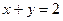
 если Д:
если Д: 
 где Д ограничена линиями:
где Д ограничена линиями: 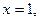

 если Д:
если Д:  где Д ограничена линиями
где Д ограничена линиями 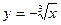
 если Д:
если Д: 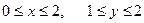
 где Д ограничена линиями
где Д ограничена линиями 
 если Д:
если Д: 

 если Д:
если Д: 
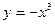
 если Д:
если Д: 
 где Д ограничена линиями
где Д ограничена линиями  если Д:
если Д: 
 где Д ограничена линиями
где Д ограничена линиями 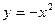
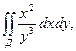 если Д:
если Д: 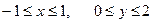
 где Д ограничена линиями
где Д ограничена линиями 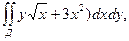 если Д:
если Д:  где Д ограничена линиями
где Д ограничена линиями  если Д:
если Д:  если Д:
если Д:  ; y = 4ex; y = 2; y = 4
; y = 4ex; y = 2; y = 4
 ; y = 2ex; y = 1; y = 2
; y = 2ex; y = 1; y = 2
 ; x = 4
; x = 4
 ; x = - y
; x = - y
 ; x = 1
; x = 1

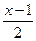
 ; y = x; x = 6
; y = x; x = 6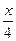 ; y = 2x; x + 3y – 7 = 0
; y = 2x; x + 3y – 7 = 0 ; y = x + 3; 2x + y – 6 = 0
; y = x + 3; 2x + y – 6 = 0
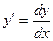 , данное уравнение перепишем в виде
, данное уравнение перепишем в виде или
или  .
. .
. .
.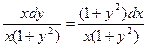


 (1)
(1) .
. .
.

 .
. .
.
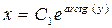

 .
.
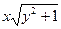


 .
.
 или
или 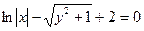 .
. .
. . Разделим обе части уравнения на хdx :
. Разделим обе части уравнения на хdx : .
.
 , т.е. функция
, т.е. функция  – однородная нулевого измерения. Тогда
– однородная нулевого измерения. Тогда 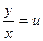 . Отсюда
. Отсюда  . Производная
. Производная  . Подставляем у¢ и u в уравнение
. Подставляем у¢ и u в уравнение  получим
получим или
или  .
. . Заменив
. Заменив 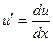 , получим
, получим  или
или  - уравнение с разделяющимися переменными. Делим его на х, получим
- уравнение с разделяющимися переменными. Делим его на х, получим 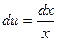 .
.
 в последнем равенстве, получим
в последнем равенстве, получим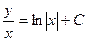 .
. .
.
 называется линейным дифференциальным уравнением первого порядка.
называется линейным дифференциальным уравнением первого порядка. ;
;  .
. , одна из которых выбирается произвольно. Если
, одна из которых выбирается произвольно. Если  , тогда
, тогда
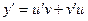


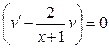
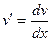
 .
.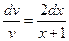

 или
или  .
. .
.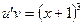 .
. .
. .
.


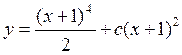
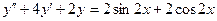
 (1). Оно отличается от соответствующего однородного линейного уравнения
(1). Оно отличается от соответствующего однородного линейного уравнения  (2) наличием в правой части некоторой функции
(2) наличием в правой части некоторой функции  .
. 
 .Их сумма есть общее решение данного неоднородного уравнения (1):
.Их сумма есть общее решение данного неоднородного уравнения (1): .
. (3) - характеристическое уравнение, соответствующее уравнению (2). Тогда если правая часть уравнения (1) имеет вид
(3) - характеристическое уравнение, соответствующее уравнению (2). Тогда если правая часть уравнения (1) имеет вид ,
, и
и  - действительные числа, а
- действительные числа, а  и
и 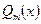 - многочлены соответственно n-й и m-й степени с действительными коэффициентами, то частное решение
- многочлены соответственно n-й и m-й степени с действительными коэффициентами, то частное решение  , (4)
, (4) и
и  - многочлены s-й степени (s– наибольшаяиз степеней n и m) с неопределенными коэффициентами. Здесь
- многочлены s-й степени (s– наибольшаяиз степеней n и m) с неопределенными коэффициентами. Здесь  - кратность корня характеристического уравнения
- кратность корня характеристического уравнения  характеристического уравнения(3). Для нахождения коэффициентов многочленов
характеристического уравнения(3). Для нахождения коэффициентов многочленов  .
.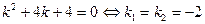 .
. для кратных корней характеристического уравнения записываем общее решение данного дифференциального уравнения:
для кратных корней характеристического уравнения записываем общее решение данного дифференциального уравнения:  .
. ,
, .
. не является корнем характеристического уравнения, то в соответствии с формулой
не является корнем характеристического уравнения, то в соответствии с формулой  частное решение будем искать в виде
частное решение будем искать в виде  , где А и В – неизвестные коэффициенты, которые нужно определить.
, где А и В – неизвестные коэффициенты, которые нужно определить. ;
; .
.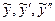 в исходное уравнение:
в исходное уравнение: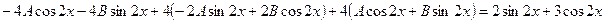
 .
. и
и  в обеих частях равенства, получаем систему
в обеих частях равенства, получаем систему ,
, и
и 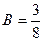 .
. .
. .
.