
|
|
VIII. ГИПОТЕЗЫ (ТЕОРИИ) ПРОЧНОСТИДо сих пор изучались расчеты на прочность, когда материал находился в одноосном напряженном состоянии (растяжение-сжатие), или в простейшем двухосном, когда напряжения в точках равны между собой и противоположны по знаку (сдвиг, кручение). Здесь составление условий прочности не вызывало затруднений: для обеспечения условий прочности требовалось, чтобы наибольшие напряжения (нормальные или касательные) не превосходили допускаемых. При изучении сложных деформаций, например, кручение с изгибом, где возникают нормальные Гипотезы прочности позволяют оценить на основании характеристик материалов, полученных при простейшем растяжении или сжатии, возможность разрушения материалов, находящихся в сложном напряженном состоянии. Напряжение одноосного растяжения, которое равноопасно заданному сложному напряженному состоянию, называют эквивалентным или приведенным ( Существуют 4 классических гипотезы прочности: 1). Первая гипотеза (теория) прочности – теория прочности наибольших нормальных напряжений. Эта теория применима только для хрупких материалов; в практических расчетах ею не пользуются. 2). Вторая гипотеза прочности – теория наибольших линейных деформаций (теория Сен-Венана). Эта теория применима только для хрупких материалов. 3). Третья теория прочности – теория прочности наибольших касательных напряжений (теория Кулона): прочность материала при сложном напряженном состоянии считается обеспеченной, если наибольшее касательное напряжение не превосходит допускаемого, установленного для одноосного напряженного состояния: По третьей теории приведенные напряжения
а приведенный момент: Эту теорию широко применяют для пластичных материалов. 4). Четвертая гипотеза прочности – теория прочности удельной потенциальной энергии изменения формы (энергетическая теория прочности): прочность материала при сложном напряженном состоянии обеспечивается в том случае, если удельная потенциальная энергия деформации не превосходит допускаемой удельной потенциальной энергии, установленной для одноосного напряженного состояния. По четвертой гипотезе (теории) прочности
а приведенный момент: Эта теория нашла наибольшее применение для пластичных материалов.
IX. РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ (продольный изгиб) Из теоретической механики известно, что равновесие абсолютно твердого тела может быть устойчивым, безразличным и неустойчивым. Например шар … .
а) Устойчивое б) Безразличное в) Неустойчивое Аналогичные примеры можно привести для равновесия деформирующихся тел (рис. 19): – так длинный стержень при действии сравнительно небольшой осевой сжимающей силы F находится в состоянии устойчивого равновесия (а); – при значении сжимающей силы F, превосходящей определенное критическое значение, прямолинейная форма равновесия становится неустойчивой и сменяется криволинейной формой равновесия, которая оказывается устойчивой (в); – наименьшее значение сжимающей силы, при котором сжатый стержень теряет способность сохранять прямолинейную форму равновесия, называется критической силой – Чтобы стержень при сжимающей нагрузке находился в прямолинейном состоянии устойчивого равновесия, необходимо, чтобы сжимающая сила была меньше критической. Допускаемая нагрузка
где
Рис. 19 Наименьшее значение критической силы
Влияние способа закрепления концов стержня На критическую силу Сжимаемый стержень может быть закреплен различным образом. Чаще всего концы стержня закрепляют одним из четырех способов (рис. 20):
Рис. 20 Способы закрепления концов стержня учитываются коэффициентом приведения длины стержня И тогда формула Эйлера выглядит так: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и касательные
и касательные 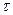 напряжения, решить задачу возможно, применяя, так называемые, гипотезы прочности.
напряжения, решить задачу возможно, применяя, так называемые, гипотезы прочности. ).
). .
.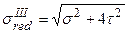 ,
, .
. ,
,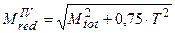 .
.
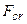 (б).
(б). при этом определяется из условия безопасности:
при этом определяется из условия безопасности: ,
,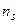 – коэффициент запаса устойчивости, который зависит от материала стержня,
– коэффициент запаса устойчивости, который зависит от материала стержня,  индекс s от stability (англ) – устойчивость
индекс s от stability (англ) – устойчивость  .
.
 .
.
 (коэффициент Ясинского).
(коэффициент Ясинского).  – приведенная длина стержня.
– приведенная длина стержня. .
.