
|
|
Интенсивностью распределённой нагрузкиПроизводная от изгибающего момента М по абсциссе x сечения балки равна поперечной силе Q: Производная от поперечной силы Q по абсциссе x сечения балки равна интенсивности распределённой нагрузки q: Отсюда вытекает, что вторая производная от изгибающего момента М по абсциссе x сечения балки равна интенсивности распределенной нагрузки q: Определение нормальных и касательных напряжений при изгибе В изогнутой балке волокна на выпуклой части растянуты, а на вогнутой – сжаты. Плоскость, в которой лежат не изменяющиеся по длине волокна, называют нейтральным слоем, т.е. в этом слое нормальные напряжения Линия пересечения нейтрального слоя с плоскостью поперечного сечения балки называется нейтральной осью (линией) (рис. 14). По закону Гука
Рис. 14
В общем случае изгиба (при поперечном изгибе) в поперечных сечениях балки наряду с изгибающим моментом М возникает поперечная сила Q. Наличие силы Q связано с возникновением в поперечных сечениях балки касательных напряжений Эти касательные напряжения Наибольшие касательные напряжения Нормальные напряжения
Условия прочности по нормальным напряжениям. Для обеспечения прочности балки необходимо, чтобы наибольшие растягивающие
где
Перемещения при изгибе. Условие жёсткости. Под действием нагрузки балки искривляются. Сечения балки перемещаются перпендикулярно и одновременно поворачиваются (рис. 15). Перемещение центра тяжести сечения по направлению перпендикулярному оси балки называется прогибом –
Рис. 15 Угол Для определения деформации балки пользуются уравнением Прогиб дифференциального уравнения изогнутой оси балки по формуле:
где l – пролет балки (рис. 15). Отсюда условие жесткости:
где В машиностроении норма допускаемого прогиба колеблется в довольно широких пределах, в зависимости от назначения детали:
VII. Кручение Стержень испытывает кручение, если в его поперечных сечениях возникают крутящие моменты Т. Эти крутящие моменты возникают под действием внешних скручивающих моментов
Рис. 16 Вращающиеся и работающие на кручение стержни называют валами. Для определения внутренних крутящих моментов Т в поперечных сечениях вала применяют метод сечений: внутренний крутящий момент Т в поперечном сечении вала численно равен алгебраической сумме внешних скручивающих моментов Для наглядного представления о характере распределения и значения крутящих моментов по длине стержня строят эпюры этих моментов. Их построение аналогично построению эпюр при растяжении или сжатии. Общепринятого правила знаков для крутящих моментов не существует. Примем следующее правило знаков (рис. 16, а):
Рис. 16, а Внутренний крутящий момент Т в сечении а-а считается положительным, когда внешний момент Рассмотрим построение эпюры внутренних крутящих моментов Т на примере рис. 16, б: вал CD, опирающийся на подшипники В и А и находящийся в равновесии под действием приложенных к нему в сечениях E. K и L внешних моментов. Сделав сечение а-а на участке DL и рассмотрев равновесие правой отсеченной части, убедимся, что Т=0.
Рис. 16, б Сделав сечение b-b на участка LK, получим из условия равновесия правой от сечения части Из построенной эпюры внутренних крутящих моментов (эТ) видно, что в местах приложения внешних крутящих моментов При наличии окружных усилий т.е. r – радиус вала. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 – (теорема Журавского).
– (теорема Журавского). .
. .
. равны нулю:
равны нулю:  .
. , т.е. при изгибе нормальные напряжения
, т.е. при изгибе нормальные напряжения  изменяются по высоте поперечного сечения балки пропорционально расстоянию y от нейтрального слоя (здесь
изменяются по высоте поперечного сечения балки пропорционально расстоянию y от нейтрального слоя (здесь  – радиус кривизны нейтрального слоя балки). Наибольшие напряжения
– радиус кривизны нейтрального слоя балки). Наибольшие напряжения  и
и  будут в наружных волокнах балки (см. рис 14).
будут в наружных волокнах балки (см. рис 14).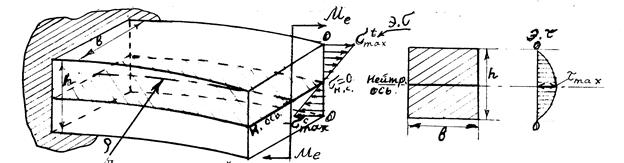
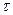 .
. , где Q – поперечная сила;
, где Q – поперечная сила;  – статический момент полуплощади поперечного сечения;
– статический момент полуплощади поперечного сечения;  – осевой момент инерции площади поперечного сечения, b – ширина площади поперечного сечения.
– осевой момент инерции площади поперечного сечения, b – ширина площади поперечного сечения.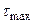 для балки прямоугольного сечения имеют место на уровне нейтральной оси (рис. 14, э
для балки прямоугольного сечения имеют место на уровне нейтральной оси (рис. 14, э  , где y – расстояние от нейтрального слоя до точки расчетного напряжения.
, где y – расстояние от нейтрального слоя до точки расчетного напряжения. напряжения при изгибе в опасном сечении, т.е. в сечении, где М имеет наибольшее по модулю значение, не превосходили допускаемых напряжений
напряжения при изгибе в опасном сечении, т.е. в сечении, где М имеет наибольшее по модулю значение, не превосходили допускаемых напряжений  и
и  :
:
 ;
;  ;
; ;
;  ,
, и
и  – расстояния от нейтрального слоя балки до наружных её волокон зон растяжения (t) и сжатия (cж);
– расстояния от нейтрального слоя балки до наружных её волокон зон растяжения (t) и сжатия (cж); – здесь значения подставляются наибольшие по абсолютному значению;
– здесь значения подставляются наибольшие по абсолютному значению; и
и  – осевые моменты сопротивления.
– осевые моменты сопротивления. .
.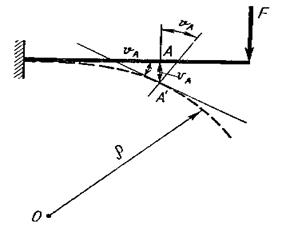
 , на который сечение поворачивается, называется углом поворота сечения.
, на который сечение поворачивается, называется углом поворота сечения. , связывающим кривизну оси балки с изгибающим моментом М и жесткостью сечения балки
, связывающим кривизну оси балки с изгибающим моментом М и жесткостью сечения балки  . Величина
. Величина  представляет собой кривизну нейтрального слоя балки.
представляет собой кривизну нейтрального слоя балки. ,
, ,
, – допускаемый прогиб балки.
– допускаемый прогиб балки. .
. (рис. 16).
(рис. 16).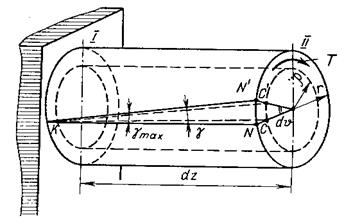
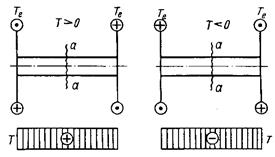
 вращает отсеченную часть против часовой стрелки, если смотреть на отсеченную часть со стороны сечения. Если же внешний момент
вращает отсеченную часть против часовой стрелки, если смотреть на отсеченную часть со стороны сечения. Если же внешний момент 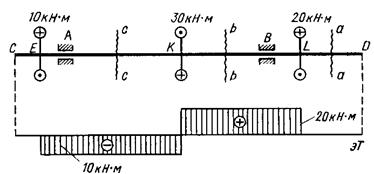
 . И, наконец, сделав сечение с-с на участке КЕ, из условия равновесия правой части получим Т=20–30=–10
. И, наконец, сделав сечение с-с на участке КЕ, из условия равновесия правой части получим Т=20–30=–10  (рис. 16, б).
(рис. 16, б). ординаты эпюры скачкообразно изменяются на величину приложенных внешних моментов.
ординаты эпюры скачкообразно изменяются на величину приложенных внешних моментов. (рис. 17), вызывающих кручение вала, предварительно вычисляют внешние скручивающие моменты
(рис. 17), вызывающих кручение вала, предварительно вычисляют внешние скручивающие моменты  , где r – расстояние от точки приложения силы
, где r – расстояние от точки приложения силы