|
|
Зависимость между моментами инерцииотносительно параллельных осей (теорема Штейнера) Определим момент инерции фигуры А относительно какой-либо оси x (рис. 10). Пусть Первый интеграл дает площадь А сечения. Второй интеграл, представляющий статический момент относительно центральной оси
Рис. 10 Момент инерции относительно центральной оси тральным моментом инерции –
Момент инерции площади сечения А относительно любой оси x равен моменту инерции относительно центральной оси Если отождествить площадь А с массой М системы, а наш центр тяжести С плоской фигуры с центром масс С системы, то наш вывод и есть суть теоремы Штейнера: момент инерции Аналогично рассуждая, момент инерции относительно оси y, параллельной центральной оси Моменты инерции простых фигур 1). Прямоугольник – центральные моменты инерции прямоугольника относительно осей 2). Круг – все центральные осевые моменты инерции площади круга одинаковы и равны:
Рис. 11 Центральный полярный момент инерции круга
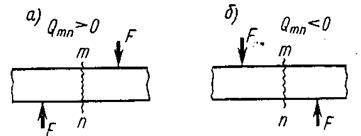
Моменты сопротивления. Основными геометрическими характеристиками, определяющими прочность стержня, являются моменты сопротивления – W. Наибольшие их значения – на наружных волокнах стержня. В расчетах обычно на них и ориентируются: – при изгибе осевой момент сопротивления или моментом сопротивления изгибу – при кручении осевой момент сопротивления Моменты сопротивления простых фигур 1). Прямоугольник – центральные моменты сопротивления прямоугольника при изгибе относительно центральных осей 2). Круг – все центральные осевые моменты сопротивления площади круга при кручении одинаковы и равны: VI. Изгиб Изгиб называется чистым, если изгибающий момент М является единственным внутренним усилием, возникающим в поперечном сечении стержня. В общем случае изгиба наряду с изгибающими моментами М в поперечных сечениях стержня возникают также и поперечные силы Q: такой изгиб называют поперечным. Стержни, работающие на изгиб, называются балками. Определение внутренних усилий при изгибе Для определения внутренних усилий – поперечной силы Q и изгибающего момента М применяют метод сечений: 1) поперечная сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от сечения; 2) изгибающий момент М в поперечном сечении балки численно равен алгебраической сумме внешних моментов Правило знаков для внутренних поперечных сил и изгибающих моментов 1). Внутренняя поперечная сила Q в сечении m-n балки считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа – сверху вниз, (рис. 12, а) и отрицательной – в противном случае (рис. 12, б):
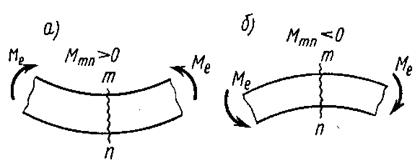
Рис. 12 2). Внутренний изгибающий момент М считается положительным, если в рассматриваемом сечении m-n балка изгибается выпуклостью вниз (рис. 13, а) и отрицательным – если выпуклостью вверх (рис. 13, б):
Рис. 13 Зависимость между изгибающим моментом, поперечной силой и 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
– центральная ось площади сечения А, параллельная оси 
. Момент инерции 
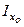относительно оси 
. Следовательно: 
.
.
системы относительно какой-либо оси х равен центральному моменту инерции 
равен: 
, где b – расстояние между параллельными осями.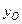
рассчитываются по формулам: 
(см4) ; 
(см4)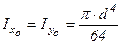
(см4) (рис. 11).
равен сумме двух осевых:
(см4).
площади поперечного сечения балки рассчитывается по формуле: 
, где 
– расстояние от нейтрального слоя балки до наружных её волокон;
, а полярный – 
, где 
– радиус вала; d – диаметр вала.
(см3); 
(см3).
(см3), а полярные – 
.
, действующих по одну сторону от данного сечения.
