
|
|
Условия прочности и жесткости при сдвигеОсновные положения и допущения. Сопротивление материалов – наука, в которой изложены принципы и методы расчета частей сооружений и машин на прочность, жёсткость и устойчивость. Расчет на прочность преследует цель подобрать выгодные размеры элементов конструкций или машин, исключающие возможность их разрушения под действием рабочих нагрузок. Расчет на жесткость связан с определением деформаций элементов конструкций или машин. Жесткость считают обеспеченной, если деформации не превосходят заданных величин, допустимых при эксплуатации конструкции. Под устойчивостью элементов сооружений подразумевают способность сохранять при действии нагрузки свою первоначальную форму. Из-за сложности задач расчета элементов конструкций в сопротивлении материалов принимается ряд допущений, упрощающих расчеты и обеспечивающих в то же время необходимую степень точности. К числу таких допущений относят: 1). Допущение об однородности и непрерывности материала, т.е. принимают, что свойства материала не зависят от формы и размеров тела и одинаковы во всех точках тела. 2). Допущение о малости рассматриваемых деформаций. Предполагают, что деформации тел под нагрузкой настолько малы, что по сравнению с размерами тел ими можно пренебречь. 3). Допущение об идеальной упругости материала. Предполагают, что материал обладает способностью полностью восстанавливать первоначальные размеры и форму после устранения нагрузок. Это допущение справедливо при ограниченных нагрузках, выше которых в материале возникают остаточные деформации, не исчезающие после удаления нагрузок. 4). Допущение называемое принципом независимости действия сил. Согласно этому принципу, результат воздействия на сооружение системы нагрузок, одновременно приложенных, равен сумме результатов воздействия тех же нагрузок, прикладываемых к телу по отдельности. 5). Допущение именуемое гипотезой плоских сечений или гипотезой Бернулли, на основании которой предполагают, что плоские сечения, проведенные в брусе до деформации, остаются плоскими и после деформации. 6). Допущение или принцип Сен-Венана: в точках тела, достаточно удаленных от мест приложения нагрузок, внутренние силы мало зависят от конкретного способа приложения этих нагрузок. Для удобства применения расчетных формул в сопротивлении материалов оговариваются и элементарные (канонические) формы тел: 1. Пластина – тело, ограниченное двумя плоскими поверхностями, т.е. два размера
Осью бруса называют линию, проходящую через центры тяжести всех его последовательно проведенных поперечных сечений. Поперечное сечение получают при рассечении бруса плоскостью перпендикулярной его оси. 4). Массив – тело, у которого все три размера соизмеримы, т.е. одного порядка:
Классификация сил сопротивления. Метод сечений.
Классификация (1). а). Силы поверхностные – силы, действующие на плоскость поверхности тела в). Объемные силы – силы, приложенные к каждой частице тела (силы тяжести, инертные силы). Классификация (2). а). Статические силы – во времени не изменяются или изменяются очень медленно. в). Динамические силы – быстро изменяются во времени.
Классификация (3). а). Силы внешние – от взаимодействия тела с окружающей средой. в). Силы внутренние – силы, вызванные действием одних частей тела на другие (силы упругости). Если на тело не действуют никакие внешние силы, то внутренние силы всё же в нем имеются: они и обеспечивают существование тела как такового. Приложение к телу внешних сил приводит к изменению внутренних сил, т.е. вследствие действия внешних сил в теле возникают дополнительные внутренние силы, вызывающие деформации. Эти силы сопротивляются стремлению внешних сил изменить форму тела, отделить одну его часть от другой. В сопротивлении материалов изучают только дополнительные внутренние силы (силы упругости), возникающие в результате деформации, вызванной внешними силами. Задача их нахождения сводится к определению равнодействующих сил и моментов, к которым приводятся в поперечном сечении эти внутренние силы упругости. Для их нахождения применяют метод сечений: 1). разделить брус на грузовые участки (с равномерной нагрузкой); 2). условно рассечь каждый грузовой участок поперечным сечением; 3). отбросить по сечению одну часть бруса; 4). приложить в сечениях усилия, способные уравновесить внешние силы, действующие на отсеченную (оставленную) часть; 5). найти значения внутренних силовых факторов из уравнения равновесия, составленные для отсеченной части. Пусть на брус действует уравновешенная система внешних сил F1, F2 … F5, расположенных в одной плоскости (рис. 1, а). Мысленно рассечем брус на две части сечением I – I и одну из частей, например, правую – отбросим (рис. 1, в). Оставшаяся левая часть под действием внешних сил окажется неуравновешенной, т.к. до рассечения бруса она уравновешивалась внутренними силами взаимодействия, передававшимися на неё с правой части. Поскольку связь между частями нарушена, необходимо для восстановления равновесия левой оставшейся части приложить по сечению I – I внутренние силы, которые заменят действие отброшенной правой части на левую. Т.к. закон распределения внутренних сил по сечению не известен, то следует воспользоваться правилами статики, т.е. привести систему внутренних сил к центру тяжести С нашего сечения и заменить внутренние силы взаимодействия статически эквивалентными векторами: главным вектором
Рис. 1 екции При пространственном расположении внешних сил (рис. 1, е) получаем шесть внутренних составляющих: три силы Составляющую внутренних сил по нормали к сечению называют нормальной или продольной силой Составляющие Момент Т относительно продольной оси скручивает брус и называется крутящим моментом: он вызывает деформацию кручения. Моменты Для определения этих шести усилий необходимо использовать шесть уравнений равновесия статики: суммы проекций всех внешних и внутренних сил и моментов, действующих на мысленно отсечённую часть бруса, соответственно на оси Деформации и перемещения Все тела под действием приложенных к ним внешних усилий в той или иной степени деформируются, т.е. изменяют свои размеры и форму. Жесткость бруса характеризуется деформацией. Изменение линейных размеров тела называется линейной, а изменение угловых размеров – угловой деформациями. Деформации, как линейные, так и угловые, могут после снятия нагрузки или полностью исчезнуть, или исчезнуть лишь частично. Деформации, исчезающие полностью после разгрузки тела, называются упругими, а свойство тел принимать после разгрузки свою первоначальную форму называется упругостью. Деформации же, сохраняемые телом и после удаления нагрузки, называются остаточными или пластическими, а свойство материалов давать остаточные деформации называется пластичностью. Зная деформации тела, можно определить перемещения всех точек тела: линейные или угловые. Для нормальной эксплуатации сооружений деформации его отдельных элементов должны быть, как правило, упругими, а вызванные ими перемещения не должны превосходить по величине определенных допускаемых значений. Эти условия, выраженные в форме тех или иных уравнений, называются условиями жёсткости. Напряжения Прочность бруса характеризуется напряжением. Чтобы связать внутренние усилия с прочностью бруса и дать оценку нагруженности бруса, необходимо определить внутренние напряжения и деформации.
Рис. 2 Выделим на нашем сечении бруса элементарную площадку Отношение Предел отношения Разлагая силу – нормальное напряжение: – касательное напряжение: Нормальное и касательное напряжения являются составляющими полного напряжения Р: очевидно, что Таким образом нормальные напряжения Напряжения имеют размерность в системе СИ паскаль: 1 Па = II. Сдвиг (срез) Под сдвигом понимают такой вид деформации, когда в поперечных сечениях стержня действует только поперечная (перерезывающая) сила Q, а остальные внутренние силовые факторы отсутствуют. Такое нагружение соответствует действию на стержень двух равных противоположно направленных и бесконечно близко расположенных поперечных сил F, вызывающих срез по плоскости, расположенной между этими силами (ножницы) (рис. 3). Срезу предшествует деформация, которая вызывается касательными напряжениями
Рис. 3 Рис. 4 Угол Закон Гука при сдвиге Экспериментально установлено, что в пределах упругости угловая деформация или угол сдвига
Условия прочности и жесткости при сдвиге Рассмотрим поперечное сечение А (рис. 5) стержня по направлению силы F. В этом сечении действует внутренняя поперечная (перерезывающая) сила Q, равная по величине силе F, но противоположно направленная: Q = F. Принимая, что касательные напряжения Таким образом, условие прочности при сдвиге:
Рис. 5 Многочисленными опытами доказано, что абсолютная величина сдвига a пропорциональна сдвигающей силе F, расстоянию h, на котором происходит сдвиг, и обратно пропорциональна площади поперечного сечения А: Из этой зависимости вытекает условие жесткости при сдвиге: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|



 и главным моментом
и главным моментом  внутренних сил, действующих в рассматриваемом сечении I – I (рис. 1, с).
внутренних сил, действующих в рассматриваемом сечении I – I (рис. 1, с).
 и
и  . Эти две неизвестные силы
. Эти две неизвестные силы 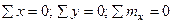 .
.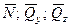 и три момента
и три момента  .
. , которая вызывает деформацию растяжения или сжатия.
, которая вызывает деформацию растяжения или сжатия. и
и  перпендикулярны нормали – их называют поперечными (перерезывающими) силами: они вызывают деформации сдвига (среза).
перпендикулярны нормали – их называют поперечными (перерезывающими) силами: они вызывают деформации сдвига (среза). и
и  изгибают брус в вертикальной и горизонтальной плоскостях и называются изгибающими моментами; они вызывают деформацию чистого изгиба. Чаще всего в поперечном сечении бруса наряду с изгибающими моментами
изгибают брус в вертикальной и горизонтальной плоскостях и называются изгибающими моментами; они вызывают деформацию чистого изгиба. Чаще всего в поперечном сечении бруса наряду с изгибающими моментами  и
и  : тогда имеет место поперечный изгиб.
: тогда имеет место поперечный изгиб. , т.е.
, т.е. , равны нулю.
, равны нулю.
 А (рис. 2), а равнодействующую внутренних сил, действующих по данной площадке, обозначим
А (рис. 2), а равнодействующую внутренних сил, действующих по данной площадке, обозначим  .
. представляет собой среднее напряжение по этой площадке.
представляет собой среднее напряжение по этой площадке. к элементу площадки
к элементу площадки  при безграничном уменьшении
при безграничном уменьшении 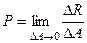 называют полным напряжением в точке по площадке
называют полным напряжением в точке по площадке 
 на составляющие: нормальную
на составляющие: нормальную  к сечению А и касательную
к сечению А и касательную  , можно определить составляющие полного напряжения Р:
, можно определить составляющие полного напряжения Р: или в общем виде
или в общем виде  ;
; и в общем виде
и в общем виде  .
. .
. стремятся сблизить или удалить отдельные частицы бруса по направлению нормали к плоскости поперечного сечения, а касательные напряжения
стремятся сблизить или удалить отдельные частицы бруса по направлению нормали к плоскости поперечного сечения, а касательные напряжения 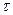 стремятся сдвинуть одни частицы тела относительно других по плоскости поперечного сечения.
стремятся сдвинуть одни частицы тела относительно других по плоскости поперечного сечения. , т.е. напряжения, это внутренняя сила, приходящаяся на единицу площади в данной точке данного сечения.
, т.е. напряжения, это внутренняя сила, приходящаяся на единицу площади в данной точке данного сечения.
 , на который изменяются прямые углы элемента dA (рис. 4) называют углом сдвига, т.е. угловой деформацией.
, на который изменяются прямые углы элемента dA (рис. 4) называют углом сдвига, т.е. угловой деформацией. – эта линейная зависимость выражает закон Гука при сдвиге. Постоянную G называют модулем сдвига или модулем упругости II рода. Он характеризует способность материала сопротивляться деформации сдвига. Единицы измерения – паскаль.
– эта линейная зависимость выражает закон Гука при сдвиге. Постоянную G называют модулем сдвига или модулем упругости II рода. Он характеризует способность материала сопротивляться деформации сдвига. Единицы измерения – паскаль. .
. .
.
 – эта формула выражает закон упругости при сдвиге, где (G·A) – жесткость стержня при сдвиге; G – модуль сдвига или модуль упругости II рода.
– эта формула выражает закон упругости при сдвиге, где (G·A) – жесткость стержня при сдвиге; G – модуль сдвига или модуль упругости II рода. .
.