Полнота интуиционистского исчисления высказываний относительно шкал Крипке
Хорошо. С формулой  справились J. Но с любой ли формулой можно справиться подобным образом? Существует ли формула, невыводимая в интуиционистском исчислении высказываний, истинная во всех мирах всех шкал, невыводимость которой, соответственно, надо доказывать как-то по-другому? Или шкалы Крипке являются окончательным ответом? справились J. Но с любой ли формулой можно справиться подобным образом? Существует ли формула, невыводимая в интуиционистском исчислении высказываний, истинная во всех мирах всех шкал, невыводимость которой, соответственно, надо доказывать как-то по-другому? Или шкалы Крипке являются окончательным ответом?
Теорема 5.4. (Полнота интуиционистского исчисления высказываний относительно шкал Крипке)
Для любой формулы, невыводимой в интуиционистском исчислении высказываний, существует шкала Крипке, в некотором мире которой эта формула ложна.
Доказательствоследует начать с определения предполагаемого стандартного вида миров.
Определение 5.2.(1)Пусть Р и Q – два конечных множества пропозициональных формул. Пару  назовём совместной, если существуют шкала Крипке и мир в ней, в котором все формулы из Р истинны, а все формулы из Q ложны. назовём совместной, если существуют шкала Крипке и мир в ней, в котором все формулы из Р истинны, а все формулы из Q ложны.
(2) Пару  назовём противоречивой, если в интуиционистском исчислении высказываний выводима формула назовём противоречивой, если в интуиционистском исчислении высказываний выводима формула  . .
Замечания.(1)Понятно, что противоречивая пара совместной быть не может. Оказывается, что верно и обратное, причём это «обратное» есть переформулировка обсуждаемой теоремы.
(2) Немного похоже на секвенции, нет?
(3) Эти пары (при одном дополнительном предположении) и будут играть роль миров в конструируемых шкалах.
Аналогом начала доказательства леммы 3.4. для данного случая является следующее утверждение.
Лемма 5.5.Пусть пара  не является противоречивой, r – произвольная формула. Тогда хотя бы одна из пар не является противоречивой, r – произвольная формула. Тогда хотя бы одна из пар  или или  также не является противоречивой. также не является противоречивой.
Доказательство.Введём обозначение (с небольшой коллизией)  , , 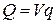 . Если обе пары противоречивы, то в интуиционистском исчислении высказываний выводимы обе импликации: . Если обе пары противоречивы, то в интуиционистском исчислении высказываний выводимы обе импликации: 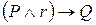 и и  . Достаточно показать, что в этом случае выводима и импликация . Достаточно показать, что в этом случае выводима и импликация  . Для этого достаточно (по лемме о дедукции) . Для этого достаточно (по лемме о дедукции)  . Поскольку, по той же лемме о дедукции, выводимость . Поскольку, по той же лемме о дедукции, выводимость  у нас уже есть, остаётся доказать, что у нас уже есть, остаётся доказать, что  . Для доказательства этого, в свою очередь, достаточно установить, что . Для доказательства этого, в свою очередь, достаточно установить, что  и и  . Первое очевидно, второе – равносильно выводимости . Первое очевидно, второе – равносильно выводимости 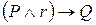 . .
QED
Замечание. Принята такая терминология: лемма 5.5. показывает, что в интуиционистской логике допустимо правило сечения, позволяющее «иссечь» формулу r из импликаций 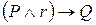 и и  , после чего от них остаётся только , после чего от них остаётся только  . .
Теперь зафиксируем некоторое конечное множество формул F, содержащее вместе с любой формулой и все её подформулы (научно говоря – замкнутое относительно перехода к подформулам).
Определение 5.3.Пусть  . Пару . Пару  будем называть полной, если она не является противоречивой и будем называть полной, если она не является противоречивой и  . .
Следующее утверждение – точный аналог леммы 3.4. очевидно следует из леммы 5.5.
Лемма 5.6. Для любой непротиворечивой пары  существует полная непротиворечивая пара существует полная непротиворечивая пара  , такая, что , такая, что  и и 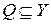 (её естественно называть расширением исходной пары). (её естественно называть расширением исходной пары).
Мирами шкалы Крипке, которую мы будем строить, являются полные непротиворечивые пары  . При этом . При этом  тогда и только тогда, когда тогда и только тогда, когда  . Интуитивный смысл этого понятен: предполагается, что в мире . Интуитивный смысл этого понятен: предполагается, что в мире  формулы множества X истинны, а формулы множества Y ложны. Это нетривиально и это придётся доказывать, но, во всяком случае, позволяет определить, какие переменные в каких мирах истинны: переменная s истинна в тех и только тех мирах, в которых формула s входит в множество X. формулы множества X истинны, а формулы множества Y ложны. Это нетривиально и это придётся доказывать, но, во всяком случае, позволяет определить, какие переменные в каких мирах истинны: переменная s истинна в тех и только тех мирах, в которых формула s входит в множество X.
Лемма 5.7.В построенной шкале в мире  истинны все формулы из X и ложны все формулы из Y. истинны все формулы из X и ложны все формулы из Y.
Доказательствопроводится индукцией по формулам. База уже есть, осталось только провести восемь вариантов индукционного перехода (четыре связки помноженные на две множества из пары).
Случай 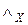 . Пусть формула . Пусть формула  входит в X. Тогда формулы s и t не могут входить в Y (иначе пара противоречива), поэтому они тоже входят в X (так как пара полна), и, по индукционному предположению, в мире входит в X. Тогда формулы s и t не могут входить в Y (иначе пара противоречива), поэтому они тоже входят в X (так как пара полна), и, по индукционному предположению, в мире  они обе истинны. Поэтому в этом мире истинна и формула они обе истинны. Поэтому в этом мире истинна и формула  . .
Случай  . Пусть формула . Пусть формула  входит в Y. Тогда по крайней мере одна из формул s или t не должна входить в X (непротиворечивость), то есть одна из них должна входить в Y (полнота). Пусть, не умаляя общности, входит в Y. Тогда по крайней мере одна из формул s или t не должна входить в X (непротиворечивость), то есть одна из них должна входить в Y (полнота). Пусть, не умаляя общности,  . Тогда она ложна в этом мире и вместе с ней ложна формула . Тогда она ложна в этом мире и вместе с ней ложна формула  . .
Связка  рассматривается аналогично (упражнение). рассматривается аналогично (упражнение).
Случай  . Пусть формула . Пусть формула  входит в X. Проверим, что она истинна в этом мире. Это означает, что в любом мире входит в X. Проверим, что она истинна в этом мире. Это означает, что в любом мире 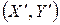 , таком, что , таком, что  , из истинности s следует истинность t. Итак, пусть s истинна в некотором таком мире. По индукционному предположению , из истинности s следует истинность t. Итак, пусть s истинна в некотором таком мире. По индукционному предположению  . С другой стороны, . С другой стороны,  . Если бы в этом случае оказалось, что . Если бы в этом случае оказалось, что 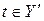 , то пара , то пара 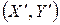 оказалась бы противоречивой, а это не так. Поэтому оказалась бы противоречивой, а это не так. Поэтому  и по индукционному предположению она истинна в мире и по индукционному предположению она истинна в мире 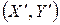 . .
Случай  .Пусть формула .Пусть формула  входит в Y. Требуется доказать, что она ложна в мире входит в Y. Требуется доказать, что она ложна в мире  . Это означает, что найдётся мир . Это означает, что найдётся мир 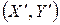 , где , где  , такой, что в нём s истинна, а t ложна, то есть , такой, что в нём s истинна, а t ложна, то есть  и и 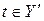 . Соответственно, надо такой мир построить. . Соответственно, надо такой мир построить.
Рассмотрим пару  . Она непротиворечива: в противном случае выводима формула . Она непротиворечива: в противном случае выводима формула  , поэтому, по лемме о дедукции выводима и формула , поэтому, по лемме о дедукции выводима и формула  , но тогда пара , но тогда пара  противоречива. противоречива.
Непротиворечивую пару можно расширить до полной, которая и будет искомым миром.
Отрицание  есть просто импликация есть просто импликация  , поэтому оно рассматривается аналогично (упражнение). , поэтому оно рассматривается аналогично (упражнение).
QED
Завершим доказательство теоремы. Пусть формула р невыводима в интуиционистском исчислении высказываний. Тогда пара  непротиворечива. Возьмём в качестве F множество всех подформул формулы р. Построим соответствующую шкалу Крипке. Полное расширение рассмотренной пары и есть тот мир, в котором будет ложна формула р. непротиворечива. Возьмём в качестве F множество всех подформул формулы р. Построим соответствующую шкалу Крипке. Полное расширение рассмотренной пары и есть тот мир, в котором будет ложна формула р.
QED
Замечание.Множество F известно, поэтому верхняя граница размера шкалы Крипке известна. Поэтому все шкалы можно перебрать, поэтому интуиционистская пропозициональная теория разрешима.
Общая картина
Интуиционистское исчисление высказываний изначально появилось как синтаксическая теория. Подобрав ей подходящую семантику, удалось (ну… практически J…) показать, что она разрешима. Тоже полезное знание J. Синтаксис и семантика – равноправные партнёры.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 справились J. Но с любой ли формулой можно справиться подобным образом? Существует ли формула, невыводимая в интуиционистском исчислении высказываний, истинная во всех мирах всех шкал, невыводимость которой, соответственно, надо доказывать как-то по-другому? Или шкалы Крипке являются окончательным ответом?
справились J. Но с любой ли формулой можно справиться подобным образом? Существует ли формула, невыводимая в интуиционистском исчислении высказываний, истинная во всех мирах всех шкал, невыводимость которой, соответственно, надо доказывать как-то по-другому? Или шкалы Крипке являются окончательным ответом? назовём совместной, если существуют шкала Крипке и мир в ней, в котором все формулы из Р истинны, а все формулы из Q ложны.
назовём совместной, если существуют шкала Крипке и мир в ней, в котором все формулы из Р истинны, а все формулы из Q ложны. .
. или
или  также не является противоречивой.
также не является противоречивой. ,
, 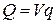 . Если обе пары противоречивы, то в интуиционистском исчислении высказываний выводимы обе импликации:
. Если обе пары противоречивы, то в интуиционистском исчислении высказываний выводимы обе импликации: 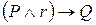 и
и  . Достаточно показать, что в этом случае выводима и импликация
. Достаточно показать, что в этом случае выводима и импликация  . Для этого достаточно (по лемме о дедукции)
. Для этого достаточно (по лемме о дедукции)  . Поскольку, по той же лемме о дедукции, выводимость
. Поскольку, по той же лемме о дедукции, выводимость  у нас уже есть, остаётся доказать, что
у нас уже есть, остаётся доказать, что  . Для доказательства этого, в свою очередь, достаточно установить, что
. Для доказательства этого, в свою очередь, достаточно установить, что  и
и  . Первое очевидно, второе – равносильно выводимости
. Первое очевидно, второе – равносильно выводимости  . Пару
. Пару  будем называть полной, если она не является противоречивой и
будем называть полной, если она не является противоречивой и  .
. и
и 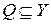 (её естественно называть расширением исходной пары).
(её естественно называть расширением исходной пары). тогда и только тогда, когда
тогда и только тогда, когда  . Интуитивный смысл этого понятен: предполагается, что в мире
. Интуитивный смысл этого понятен: предполагается, что в мире 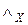 . Пусть формула
. Пусть формула  входит в X. Тогда формулы s и t не могут входить в Y (иначе пара противоречива), поэтому они тоже входят в X (так как пара полна), и, по индукционному предположению, в мире
входит в X. Тогда формулы s и t не могут входить в Y (иначе пара противоречива), поэтому они тоже входят в X (так как пара полна), и, по индукционному предположению, в мире  . Пусть формула
. Пусть формула  . Тогда она ложна в этом мире и вместе с ней ложна формула
. Тогда она ложна в этом мире и вместе с ней ложна формула  рассматривается аналогично (упражнение).
рассматривается аналогично (упражнение). . Пусть формула
. Пусть формула  входит в X. Проверим, что она истинна в этом мире. Это означает, что в любом мире
входит в X. Проверим, что она истинна в этом мире. Это означает, что в любом мире 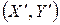 , таком, что
, таком, что  , из истинности s следует истинность t. Итак, пусть s истинна в некотором таком мире. По индукционному предположению
, из истинности s следует истинность t. Итак, пусть s истинна в некотором таком мире. По индукционному предположению  . С другой стороны,
. С другой стороны,  . Если бы в этом случае оказалось, что
. Если бы в этом случае оказалось, что 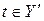 , то пара
, то пара  и по индукционному предположению она истинна в мире
и по индукционному предположению она истинна в мире  .Пусть формула
.Пусть формула  . Она непротиворечива: в противном случае выводима формула
. Она непротиворечива: в противном случае выводима формула  , поэтому, по лемме о дедукции выводима и формула
, поэтому, по лемме о дедукции выводима и формула  , но тогда пара
, но тогда пара  есть просто импликация
есть просто импликация  , поэтому оно рассматривается аналогично (упражнение).
, поэтому оно рассматривается аналогично (упражнение). непротиворечива. Возьмём в качестве F множество всех подформул формулы р. Построим соответствующую шкалу Крипке. Полное расширение рассмотренной пары и есть тот мир, в котором будет ложна формула р.
непротиворечива. Возьмём в качестве F множество всех подформул формулы р. Построим соответствующую шкалу Крипке. Полное расширение рассмотренной пары и есть тот мир, в котором будет ложна формула р.