
|
|
Предварительное обсуждениеПростой алгоритм проверки принадлежности формулы пропозициональной теории, приведённый в §1, хорош не во всех отношениях. Если вспомнить основную цель исследования – изучение человеческого мышления, то недостаток алгоритма становится понятен: люди думают не так. Они используют умозаключения, а не полный перебор различных вариантов (он «несолиден» и обычно нереален из-за высокой трудоёмкости). Формальный аналог умозаключения называется правилом вывода, а система, позволяющая производить последовательные выводы – исчислением. При этом любое умозаключение должно начинаться с какой-то посылки, значит, должны быть некоторые исходные посылки, принимаемые на веру, некритически, с которых всё начинается – аксиомы. Итак, для задания исчисления необходимо и достаточно задать его аксиомы и правила вывода. При этом важно, чтобы относительно любой формулы можно было бы за конечное время определённо выяснить, является ли она аксиомой; другими словами – теория А, состоящая из аксиом (аксиоматика), должна быть разрешимой. Для задания необходимой аксиоматики не то, чтобы потребуется, но – окажется очень удобна – ещё одна логическая связка – импликация. Она, конечно, выражается через уже имеющиеся:
Аксиоматика Определение 2.1. Аксиомой исчисления высказываний называется любая формула, имеющая один из тринадцати видов: (А1) (А2) (А3) (А4) (А5) (А6) (А7) (А8) (А9) (А10) (А11) (А12) (А13) где а, b, с – произвольные формулы. Замечания.(1) Почему приведённая аксиоматика разрешима? Потому что существует алгоритм (обычно именуемый синтаксическим анализом) который позволяет проверить, имеет ли некоторое выражение один из тринадцати приведённых выше видов (для начала посмотрим, начинается ли слово с буквы J или D, затем выделим фрагменты, соответствующие аргументам этой булевой функции и т.д.). (2) Выражения (А1) – (А13) обычно называют схемами аксиом. Их конечное число. Конкретные аксиомы получаются из схем заменой переменных а, b, с на конкретные формулы, поэтому множество всех аксиом бесконечно. Соответственно, и количество аксиом бесконечно. Важно также отметить, что а, b, с – не пропозициональные переменные, они принимают значения не из множества высказываний, а из множества формул. Такие переменные можно назвать формульными. (3) От вхождения «лишнего» символа J можно избавиться, заменив все его вхождения «обратно» на DN. Например, аксиома (А8) превратится при этом в «настоящую» формулу (4) С другой стороны, использование символа J упрощает аксиомы, но ещё не делает их интуитивно понятными (что было бы крайне желательным) L. В этом смысле определение 2.1. представляет собой самый настоящий «персидский компромисс». Для того чтобы радикально повысить их интуитивную очевидность, можно использовать любой естественный символ импликации: (А1) (А2) (А3) (А4) (А5) (А6) (А7) (А8) (А9) (А10) (А11) (А12) (А13) В таком виде аксиомы действительно являются интуитивно очевидными J. (5) Список схем аксиом из определения 2.1. не является единственно возможным для построения исчисления высказываний. Он даже не является минимальным! В действительности можно, основываясь на полном наборе булевых функций, состоящем из импликации и тождественного нуля, построить аксиоматику, основанную всего на трёх схемах аксиом. Определение 2.1'.Аксиомой исчисления высказываний называется любая формула, имеющая один из трёх видов: (В1) (В2) (В3) При этом аксиомы вида (А3) – (А13) станут теоремами (что бы ни означало это слово).
Правило вывода Закончив обсуждение аксиоматики, перейдём к правилам вывода. В исчислении высказываний такое правило всего одно, оно называется modus ponens. Его обычно записывают в форме (МР) Фактически оно является тернарным отношением на множестве формул, но эту формальность можно отдельно не обсуждать, поместив её «внутри» определений формального вывода и теоремы.
Доказательство. Теорема Определение 2.2.(1) Последовательность формул (2) Формула, имеющая доказательство, называется теоремой исчисления высказываний. Пример.Покажем, что для любой формулы p формула ( ( ( ( ( Замечания.(1)В приведённом рассуждении р является формульной переменной. Соответственно, выше написаны гораздо более содержательные вещи, чем просто формулы и доказательство, именно: схемы формул и схема доказательства. Конкретное доказательство формулы (2) Теорема
Вывод. Выводимость В действительности мышление устроено ещё чуть-чуть сложнее. Повседневная практика показывает, что только самые простые теоремы выводятся из одних лишь аксиом. Дальнейшая мыслительная деятельность предполагает возможность получения новых теорем из старых. Другими словами, уже доказанные теоремы можно использовать как новые аксиомы. Определение 2.3.(1)Пусть (2) В описанной ситуации говорят, что формула (3) Формула d является теоремой тогда и только тогда, когда Лемма 2.1.Пусть Доказательство.Вывод тривиально превращается в доказательство: достаточно вместо посылки QED Замечание. Однако вполне возможно, что среди посылок встречаются формулы, не являющиеся ни теоремами, ни даже тавтологиями. Понятие вывода от этого не теряет своей осмысленности. У множества формул, которые можно получить как результат таких «незаконных доказательств», даже есть свой наглядный смысл: в него могут входить только те высказывания, которые получаются, если подставлять вместо пропозициональных переменных не «какие попало» наборы простых высказываний, а только такие, которые не делают ложной ни одну использованную посылку. Можно сказать, что вывод – это «условное» доказательство (в противовес доказательству обычному, «безусловному»), а его результат – «условная тавтология». Сделанное соображение крайне важно, и в дальнейшем будет сильно обобщено, поэтому полезно оформить его в виде определения.
Определение 2.4.Пусть Р – множество формул, q – формула. Если любой набор значений переменных, обращающий все формулы множества Р в истины, обращает в истину и q, то говорят, что q семантически следует из Р и пишут Использование этого определения позволяет уточнить замечание. Теорема 2.2.(оправданность аксиоматизации)
Доказательство.Индукция по длине вывода, т.е. по количеству формул в выводе. Если длина вывода равна 1, то его единственная формула – либо аксиома (которая является тавтологией), либо посылка (которая тривиально истинна на любом наборе значений, на котором истинны все посылки). Поэтому в этом случае утверждение тривиально. Тем самым база доказана. Пусть длина вывода равна n, сам вывод есть QED 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
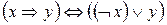 . Соответственно, полезно модифицировать рассматриваемый алфавит, добавив к нему новый символ J, заменяющий буквосочетание DN:
. Соответственно, полезно модифицировать рассматриваемый алфавит, добавив к нему новый символ J, заменяющий буквосочетание DN:  .
. ,
, ,
, ,
, ,
, ,
, ,
,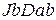 ,
,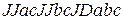 ,
, ,
,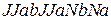 ,
,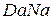 ,
,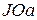 ,
,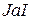 ,
, .
. ,
,  или
или 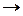 . Все они, так или иначе, используются в метаязыке, так что его использование нарушит одно из используемых соглашений. Кроме того, это исключит возможность использования свойств «польской записи», так что для установления порядка выполнения логических операций придётся использовать скобки (обычным образом). Тем не менее, сделаем это, используя символ
. Все они, так или иначе, используются в метаязыке, так что его использование нарушит одно из используемых соглашений. Кроме того, это исключит возможность использования свойств «польской записи», так что для установления порядка выполнения логических операций придётся использовать скобки (обычным образом). Тем не менее, сделаем это, используя символ 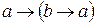 ,
,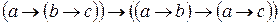 ,
,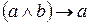 ,
,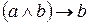 ,
,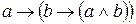 ,
, ,
, ,
,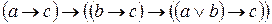 ,
, ,
, ,
,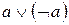 ,
,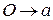 ,
, .
.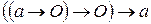 .
. .
.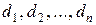 называется доказательством, или, точнее – доказательством формулы
называется доказательством, или, точнее – доказательством формулы  , если
, если  формула
формула  есть либо аксиома, либо формула q, такая, что
есть либо аксиома, либо формула q, такая, что  такие, что
такие, что  ,
,  (это и есть использование правила (МР)).
(это и есть использование правила (МР)). является теоремой. Её доказательством может, например, служить следующая последовательность:
является теоремой. Её доказательством может, например, служить следующая последовательность: )
)  (частный случай аксиомы (А1));
(частный случай аксиомы (А1)); )
) 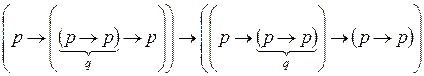 (частный случай аксиомы (А2));
(частный случай аксиомы (А2)); )
)  (следует из
(следует из 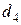 )
) 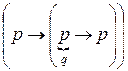 (частный случай аксиомы (А1));
(частный случай аксиомы (А1)); )
)  для каждой данной формулы q получается, если подставить её вместо формульной переменной р в указанную схему.
для каждой данной формулы q получается, если подставить её вместо формульной переменной р в указанную схему. – некоторый набор формул. Элементы множества Р принято называть посылками. Последовательность формул
– некоторый набор формул. Элементы множества Р принято называть посылками. Последовательность формул  .
. . Обычно символ
. Обычно символ 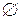 принято опускать и писать более коротко:
принято опускать и писать более коротко:  .
. вставить доказательство теоремы
вставить доказательство теоремы  .
.
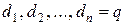 и для любого
и для любого  известно, что
известно, что 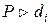 . Если
. Если 
 и
и 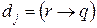 . По индукционному предположению
. По индукционному предположению  и
и  . Соответственно, если на данном наборе аргументов все посылки истинны, то на нём истинны и формулы r и
. Соответственно, если на данном наборе аргументов все посылки истинны, то на нём истинны и формулы r и 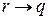 . Следовательно, на этом наборе аргументов истинна и формула q (так как при истинном значении r единственный способ сделать импликацию истинной – это сделать истинной формулу q).
. Следовательно, на этом наборе аргументов истинна и формула q (так как при истинном значении r единственный способ сделать импликацию истинной – это сделать истинной формулу q).