
|
|
Высказывания, простые и составныеЛюбое рассуждение состоит из высказываний. Высказывание удобно воспринимать как неопределяемое понятие – как утверждение, про которое можно определённо сказать, что оно является либо безусловно истинным, либо безусловно ложным. При этом возможно, что неизвестно – истинно или ложно в действительности (в данный момент или в принципе навсегда) некоторое конкретное высказывание. Таковы, например, высказывания «Бог существует» и «В десятичной записи числа π содержится бесконечно много девяток». Абстрагируясь от «особенностей текста», высказывание можно воспринимать как логическую константу с известным или неизвестным значением. Напротив, в силу отчётливо выраженного условного характера, высказываниями не являются, например, фразы «бог существует» (написание с маленькой буквы уничтожает недвусмысленную ссылку на христианского творца и требует уточнения – какой именно бог имеется в виду) и «x делится на 5» (истинность этого утверждения зависит от значения, принимаемого переменной x). Высказывания можно комбинировать, создавая из нескольких высказываний новое при помощи так называемых логических связок. Например, из высказываний «Сборная России по футболу – действующий чемпион мира» и «Ныне здравствующий Папа Римский по национальности – индеец сиу» можно построить ещё несколько высказываний: «Сборная России по футболу – действующий чемпион мира и ныне здравствующий Папа Римский по национальности – индеец сиу», «Если сборная России по футболу – действующий чемпион мира, то ныне здравствующий Папа Римский по национальности – индеец сиу», «Либо сборная России по футболу – действующий чемпион мира, либо ныне здравствующий Папа Римский по национальности – индеец сиу». Заметим, что одно из этих высказываний даже является истинным J. В некотором содержательном смысле логические связки тождественны булевым функциям, рассмотренным в курсе дискретной математики. Многие даже рассматривают теорию булевых функций как раздел математической логики, и эта точка зрения по-своему оправданна. Однако основным лейтмотивом теории булевых функций является проблема конструирования одних функций из других (при этом возможны различные способы: формулы, схемы…), в то время как математическая логика изучает принципиально иные вопросы. Ниже будет изложен логический аспект теории булевых функций, который обычно называют пропозициональной логикой. При этом обычная теория (СДНФ, теорема Поста, концепция сложности и т.д.) считается известной и не обсуждается, если к этому не приводит изучение чисто логических вопросов.
Алфавит Во-первых, рассмотрим множество Ω всех высказываний. Переменные, принимающие значения из множества Ω, будем называть пропозициональными переменными и обозначать маленькими латинскими буквами. Множество всех пропозициональных переменных обозначим буквой V. Заметим, что термин «множество всех пропозициональных переменных» (так же, собственно, как и «множество всех высказываний»), строго говоря, математически некорректен, так как V обладает некоторыми свойствами, противоречащими обычному пониманию термина «множество». Например, для любого «настоящего» множества пропозициональных переменных найдётся переменная, в него не входящая, а V таким свойством не обладает, так как в V входят все пропозициональные переменные. Вместе с некоторым набором символов логических связок множество V составляет алфавит языка пропозициональной логики. Этот набор символов (сигнатура) может быть принят любым. Для простоты на начальный период этого обсуждения примем его равным
Формальный язык Во-вторых, определим формальный язык L, по существу – совпадающий с множеством формул (в данном случае – в базисе Определение1.1.Множество (слов) L называется (а множество слов принято обычно называть формальным языком) множеством формул пропозициональной логики, если оно удовлетворяет условиям: (1) однобуквенные слова O и I принадлежат языку L; (2) любое однобуквенное слово вида x, где (3) если (4) если (5) если W – формальный язык, удовлетворяющий условиям (1) – (4), то Замечания.(1)Определения, аналогичные приведённому выше, называются индуктивными, а аксиомы, подобные (5) – аксиомами индукции. (2) Само существование языка L – не такой уж тривиальный вопрос (возможно, его задекларированные свойства каким-то образом противоречат друг другу!). (3) В действительности L – (универсальная) алгебра, в рассматриваемом случае – с пятью операциями (двумя нульарными, одной унарной и двумя бинарными), естественным образом соответствующим элементам функционального базиса. Пример.Формулу (4) Эта запись, являясь вариантом так называемой «польской записи», позволяет избежать появления скобок. Теорема 1.1. Язык L существует и единственен. Доказательство.Заметим, что формальные языки, обладающие свойствами (1) – (4) существуют. Например, таковым является множество всех слов над рассматриваемым алфавитом, или – над любым бòльшим алфавитом. Пусть Далее, заметим, что Покажем, что этот язык обладает также и свойством (5). Пусть это не так, то есть Осталось доказать единственность языка L. Пусть QED Примеры. (1) По какой причине формулой является выражение (2) Почему формулой не является никакое выражение, содержащее некоторый символ, не входящий в (3) Почему формулой не является выражение
Пропозициональная теория В третьих, определим некоторое подмножество Т языка L. Для этого необходимо вспомнить, что использованные буквы Определение 1.2.(1)Пусть (2) Множество всех тавтологий обозначим буквой Т. (3) Пара Замечание.Описания, аналогичные определению 1.2, называются семантическими, то есть – «основанными на смысле». Повторимся. Множество L есть множество формул, т.е. осмысленных выражений, а множество Т – множество теорем (теория), истинных осмысленных утверждений. Основной вопрос, рассматриваемый в описанном контексте, – вопрос принадлежности некоторого элемента языка L языку Т, то есть – об истинности некоторого осмысленного утверждения. В данном случае этот вопрос тривиально решается при помощи составления таблицы истинности. Причина, по которой можно составить таблицу истинности, проста, но заслуживает того, чтобы её сформулировали: множество Ω является очень большим и сложно устроенным, но про его элементы нам требуется знать отнюдь не всё, достаточно только знать, истинно ли некоторое высказывание или оно ложно. Поэтому можно отождествить все истинные высказывания, равно как и все ложные, и вместо плохого множества Ω рассмотреть хорошее и простое множество Следовательно, таблицу истинности сложного высказывания, зависящего от n простых (кстати, не вполне ясно, что это такое J), можно составить перебором всего лишь Пример. Покажем, что уже рассмотренная формула
Формула не является тавтологией, так как на одном, по меньшей мере, наборе аргументов принимает значение 0. Естественно, соответствующий набор аргументов для любой рассматриваемой формулы, если он существует, не угадывается, а находится в процессе полного перебора (который определённо закончится в некоторый момент). Совершенно очевидно, что для любой осмысленной формулы соответствующие вычисления происходят аналогично и не могут «не получиться». Как раз это и означает, что существует алгоритм проверки того, является ли некоторая формула тавтологией. В подобных случаях говорят, что теория Т разрешима. Итак, имеет место теорема: Теорема 1.2. Пропозициональная теория разрешима. QED Стоит отметить, что разрешима далеко не любая теория. Причиной разрешимости конкретно пропозициональной теории является её крайняя простота.
Общая картина Какое место в общей картине занимают рассмотренные объекты? В рассматриваемой модели они играют роль реального мира, в котором есть вещи мыслимые, но неизвестно, верные ли (язык L), а есть – «правда жизни» (язык Т). Теории, заданные ссылкой на «объективную реальность», называются семантическими. В следующем параграфе будет сформулировано понятие, играющее в рассматриваемой модели роль мышления. Исчисление высказываний 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (этот набор полон, что следует из существования СДНФ, поэтому он может быть модифицирован в любой другой).
(этот набор полон, что следует из существования СДНФ, поэтому он может быть модифицирован в любой другой). (соответствие между наборами очевидно).
(соответствие между наборами очевидно).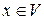 , принадлежит языку L (можно не вполне точно прописать:
, принадлежит языку L (можно не вполне точно прописать:  );
); , то
, то  ;
; , то
, то 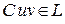 и
и 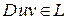 ;
;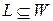 .
. можно воспринимать как результат применения бинарной операции С к формулам
можно воспринимать как результат применения бинарной операции С к формулам  и
и 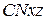 :
:  .
. – множество всех формальных языков, удовлетворяющих этим свойствам (это опять не совсем «правильное» множество, но мы не будем обращать на это внимания).
– множество всех формальных языков, удовлетворяющих этим свойствам (это опять не совсем «правильное» множество, но мы не будем обращать на это внимания). формальный язык
формальный язык 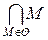 , состоящий из тех и только тех слов, которые входят во все языки множества
, состоящий из тех и только тех слов, которые входят во все языки множества  , также обладает указанными свойствами. Действительно, если, например,
, также обладает указанными свойствами. Действительно, если, например,  , то это означает, что
, то это означает, что 
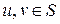 , следовательно
, следовательно 
 . Очевидно, что в случае остальных условий, которые необходимо проверить, рассуждения абсолютно аналогичны. В частности, свойствами (1) – (4) обладает формальный язык
. Очевидно, что в случае остальных условий, которые необходимо проверить, рассуждения абсолютно аналогичны. В частности, свойствами (1) – (4) обладает формальный язык  .
. , такой, что
, такой, что  . Тогда
. Тогда  . Полученное противоречие доказывает рассматриваемое утверждение.
. Полученное противоречие доказывает рассматриваемое утверждение. – другой формальный язык, удовлетворяющий свойствам (1) – (5). Тогда он, в частности, удовлетворяет свойствам (1) – (4), поэтому
– другой формальный язык, удовлетворяющий свойствам (1) – (5). Тогда он, в частности, удовлетворяет свойствам (1) – (4), поэтому  (по свойству (5) языка L). Симметричным образом,
(по свойству (5) языка L). Симметричным образом,  , откуда
, откуда  .
. (то есть
(то есть  )? По той, что она имеет вид
)? По той, что она имеет вид  , где
, где  и
и  являются формулами (свойство (4)). Выражение А, в свою очередь является формулой потому, что имеет вид
являются формулами (свойство (4)). Выражение А, в свою очередь является формулой потому, что имеет вид  , где
, где  является формулой в силу свойства (2). Тот факт, что выражение В тоже является формулой также следует из того, что свойства (3) и (4) позволяют свести его к тому, что формулами являются x, y, и z.
является формулой в силу свойства (2). Тот факт, что выражение В тоже является формулой также следует из того, что свойства (3) и (4) позволяют свести его к тому, что формулами являются x, y, и z. ? Потому что существует формальный язык, удовлетворяющий условиям (1) – (4) и не содержащий ни одного слова, в который входит этот «лишний» символ (например – множество всех слов над алфавитом
? Потому что существует формальный язык, удовлетворяющий условиям (1) – (4) и не содержащий ни одного слова, в который входит этот «лишний» символ (например – множество всех слов над алфавитом  ,
, 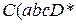 и
и 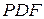 . Отметим одну сравнительно тонкую и малозаметную деталь: в первой «не-формуле» x и y являются не пропозициональными, а, например, действительными переменными, то есть они похожи на элементы V, но таковыми не являются.
. Отметим одну сравнительно тонкую и малозаметную деталь: в первой «не-формуле» x и y являются не пропозициональными, а, например, действительными переменными, то есть они похожи на элементы V, но таковыми не являются. ? Потому что множество всех слов над алфавитом
? Потому что множество всех слов над алфавитом  удовлетворяет условиям (1) – (4), значит
удовлетворяет условиям (1) – (4), значит  (из множества всех слов в этом случае следует исключить два:
(из множества всех слов в этом случае следует исключить два:  ). И уже по этой причине формулой не является и рассматриваемое выражение
). И уже по этой причине формулой не является и рассматриваемое выражение  , а также (менее точно) множество Т, называется пропозициональной теорией.
, а также (менее точно) множество Т, называется пропозициональной теорией. .
. возможных наборов аргументов. На каждом наборе аргументов вычисление проводится непосредственно, притом – чисто «грамматическими» средствами (далее мы будем называть такие вычисления «синтаксическими»). Поэтому можно сказать, что существует алгоритм проверки того, является ли слово u языка L также словом языка Т.
возможных наборов аргументов. На каждом наборе аргументов вычисление проводится непосредственно, притом – чисто «грамматическими» средствами (далее мы будем называть такие вычисления «синтаксическими»). Поэтому можно сказать, что существует алгоритм проверки того, является ли слово u языка L также словом языка Т.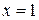 ,
,  ,
,  . Проведём непосредственное вычисление:
. Проведём непосредственное вычисление: .
.