
|
|
Транзитивность выводимостиСледует отметить ещё одно свойство выводимости, которое тривиально обобщает лемму 2.1. и доказывается совершенно так же. Лемма 2.3.(Транзитивность выводимости) Пусть Р и Q – два множества формул,
Теорема о дедукции для исчисления высказываний Семантическое следование родственно импликации: импликация есть как раз булева функция, выражающая свойство одних высказываний «семантически следовать» из других. Неудивительно поэтому, что импликации родственна и выводимость – синтаксический аналог семантического следования. Теорема 2.4.(Лемма о дедукции для исчисления высказываний) Для любого множества формул Р и для любых формул q и r равносильны условия: (1) (2) Замечание.Вместо Доказательство.Импликация (2) Доказательство импликации (1) Шаг 1. Напишем последовательность формул Шаг 2. Возможно, некоторые формулы Шаг 3. Возможно, некоторые формулы
Тогда формула Шаг 4. Возможно, некоторые формулы
Теперь и формула Заметим, что проведение этих шагов делает формулы последовательности (**) «всё более и более доказанными», а последний шаг просто превращает эту последовательность в вывод. QED Замечание.Практическое использование импликации (1)
Общая картина Вывод является достаточно адекватным аналогом процесса мышления (и даже может быть основан на неверных посылках J). Теории, построенные на основе различных вариантов выводов, и, соответственно, состоящие из теорем, называются синтаксическими. Основной предмет изучения в математической логике – соотношение между синтаксисом и семантикой.
Полнота исчисления высказываний Мотивировка С самого момента изобретения дедуктивного метода (то есть – со времён Евклида, а не Шерлока Холмса! J) математики мечтали установить важнейший факт: любое истинное утверждение может быть доказано. Нельзя сказать, что в противном случае математика стала бы намного менее осмысленным занятием, но, занимаясь поисками доказательства некоторого (допустим – откуда-то известно, что верного) утверждения крайне приятно было бы знать, что таковое существует. С точки зрения моделирования процесса человеческого мышления этот факт означал бы что «до всякой правды можно додуматься». Жизнь показала, что во многих случаях всё сложнее, но иногда этот факт всё-таки имеет место. В этом случае говорят, что в рассматриваемой ситуации имеет место теорема о полноте соответствующего исчисления. В этом параграфе будет показано, что для исчисления высказываний теорема о полноте верна. Итак, имеет место теорема. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 ,
, 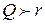 . Тогда
. Тогда 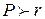 .
.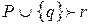 ;
;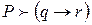 .
. удобно писать P, q. В дальнейшем будет использоваться именно такая запись.
удобно писать P, q. В дальнейшем будет использоваться именно такая запись. (1) тривиальна. Действительно, пусть
(1) тривиальна. Действительно, пусть  – вывод формулы
– вывод формулы  из набора посылок Р. Тогда
из набора посылок Р. Тогда  – вывод формулы r из набора посылок Р, q: формула
– вывод формулы r из набора посылок Р, q: формула 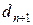 – одна из посылок, а формула
– одна из посылок, а формула  есть результат применения правила МР к формулам
есть результат применения правила МР к формулам  .
. (*) – вывод формулы r из набора посылок Р, q. Построим, исходя из него вывод формулы
(*) – вывод формулы r из набора посылок Р, q. Построим, исходя из него вывод формулы  из набора посылок Р. Сделаем это в несколько шагов.
из набора посылок Р. Сделаем это в несколько шагов. (**). Разумеется, эта последовательность формул не является выводом. Для того чтобы сделать её таковым, вставим в неё ещё некоторые формулы.
(**). Разумеется, эта последовательность формул не является выводом. Для того чтобы сделать её таковым, вставим в неё ещё некоторые формулы. просто равны q. Тогда формула
просто равны q. Тогда формула  есть просто формула
есть просто формула  , которая является теоремой исчисления высказываний. Вставим перед первой такой формулой её доказательство.
, которая является теоремой исчисления высказываний. Вставим перед первой такой формулой её доказательство. являются аксиомами исчисления высказываний или посылками из Р. Вставим перед каждой такой формулой ещё две:
являются аксиомами исчисления высказываний или посылками из Р. Вставим перед каждой такой формулой ещё две: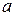 – посылка или аксиома;
– посылка или аксиома; – аксиома (А1).
– аксиома (А1). становится результатом применения к ним правила МР.
становится результатом применения к ним правила МР.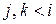 , такие, что
, такие, что  ,
,  ,
,  . Соответственно, в последовательности (**) есть формулы
. Соответственно, в последовательности (**) есть формулы  , которые можно использовать для вывода формулы
, которые можно использовать для вывода формулы  . Вставим перед последней формулой ещё две формулы:
. Вставим перед последней формулой ещё две формулы: – аксиома (А2);
– аксиома (А2); – результат применения правила МР.
– результат применения правила МР. . Существует ещё несколько «ходовых» дробей такого вида, например:
. Существует ещё несколько «ходовых» дробей такого вида, например: ,
,  ,
, 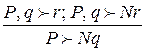 . Все они соответствуют утверждениям, подобным лемме о дедукции (но более простым) и доказываются с использованием соответствующих аксиом (каких? как?) совершенно аналогично доказательству импликации (2)
. Все они соответствуют утверждениям, подобным лемме о дедукции (но более простым) и доказываются с использованием соответствующих аксиом (каких? как?) совершенно аналогично доказательству импликации (2)