
|
|
Теорема 3.1. (Теорема о полноте исчисления высказываний)Формула выводима в исчислении высказываний тогда и только тогда, когда она является тавтологией. Символически: Первое доказательство Естественно предположить, что имеет место более сильное утверждение: Позднее мы покажем, что импликация (*) действительно верна. Однако простейшее доказательство теоремы о полноте основано на её более изысканном аналоге. Определение 3.1.Пусть Лемма 3.2.Пусть q – формула, содержащая переменные Замечание. Родство сформулированного утверждения с гипотезой (*) несомненно, но описанное свойство всё-таки «информативнее» семантического следования (утверждается, что из формул Доказательстволеммы можно провести индукцией по множеству формул. Индукционный переход состоит в доказательстве большого количества однотипных выводимостей, представляющих собой синтаксические аналоги определений соответствующих булевых функций: а) Первая выводимость:
б) Во многих случаях построение выводов основано на одной из «дробей», приведённых в замечании к лемме о дедукции, именно – на правиле Согласно лемме о дедукции, если
в) Докажем выводимость
г) Докажем ещё одно правило из замечания к лемме о дедукции, именно –
д) Докажем ещё одно правило: для любой формулы
е) Докажем выводимость Итак, можно считать, что все требуемые выводимости доказаны. Для завершения доказательства леммы осталось заметить, что любая формула имеет некоторую «самую внешнюю» операцию, которую одна из выводимостей позволяет снять, сведя выводимость рассматриваемой формулы к выводимостям для более простых формул (которые можно считать доказанными по индукционному предположению). В конце концов выводимость данной тавтологии сведётся к выводимостям для тривиальных формул вида y (переменная). Все такие выводы тривиальны. QED Доказанная лемма показывает, как можно построить доказательство любой тавтологии. Для этого достаточно: а) пользуясь доказанными правилами, построить выводы рассматриваемой тавтологии из всевозможных наборов посылок б) разбить все выводы на пары, отличающиеся, единственно, посылкой, относящейся к первой переменной (в первом выводе пары использована посылка в) пользуясь пунктом г доказательства леммы, объединить эти пары в выводы, не содержащие посылок, относящихся к первой переменной; г) поступить аналогично с остальными переменными по очереди. Ясно, что в конце процедуры будет получен вывод без посылок, т.е. обыкновенное доказательство. QED Замечания.(1) Предъявленное доказательство – конструктивное. Оно показывает, как можно построить доказательство любой тавтологии (правда, способ построения ужасен L). (2) В том случае, когда доказываемое утверждение (например, по ошибке) тавтологией не является, это обстоятельство обнаружится при построении доказательства, а не будет выступать как «непонятное препятствие», «почему-то не позволяющее построить» требуемое доказательство J. (3) Рассмотренное доказательство полезно сравнить с примером, рассмотренным в §1 и с материалом следующего параграфа.
Второе доказательство В этом пункте будет доказано обещанное ранее более сильное утверждение Начать следует с набора интуитивно ясных определений, конкретизирующих как семантический, так и синтаксический аспекты понятия «противоречивость». Определение 3.2.(1) Множество Р булевых формул называется совместным, если существует набор значений переменных, входящих в них, при котором все формулы, входящие в Р, истинны. (2) В противном случае множество Р называется несовместным. Это – семантическое определение противоречивости (в формулы семейства Р нельзя подставить что-то такое, что сделает их истинными одновременно, некоторая формула обязательно окажется ложной и будет противоречить в этом смысле тем, которые случайно оказались истинными; формулы семейства Р, тем самым, противоречат друг другу). Заметим, что формула q является тавтологией тогда и только тогда, когда набор формул (состоящий из одной формулы, а что тут такого!? J) (3) Формула q называется выполнимой, если соответствующая булева функция не есть тождественная ложь. Заметим, что формула является тавтологией тогда и только тогда, когда её отрицание не является выполнимой формулой. (4) Множество формул Р называется противоречивым, если существует формула q, такая, что
О (МР). Верно и обратное: как только формула О доказана, становится возможным доказать что угодно, в том числе и два противоположных утверждения (тривиально используя аксиому (А12)). Поэтому для констатации противоречивости множества можно использовать запись Теорема 3.3. Доказательствонепротиворечивости совместного множества совсем просто: в противном случае на наборе аргументов, обращающем в истины все формулы множества Р, обязана была бы оказаться истинной и формула О, а это невозможно. Доказательство обратного утверждения существенно сложнее. Пусть Р – непротиворечивое множество формул. Требуется предъявить набор значений входящих в них переменных, на котором все формулы из Р истинны. Иногда соответствующее значение переменной очевидно. Если переменная x такова, что а) как-то определить значения остальных переменных; б) после этого не забыть убедиться, что полученный набор действительно является «хорошим»: отмеченные условия на значения переменных необходимы, но, возможно, не достаточны! Пункт а исполняется очень радикально J. За счёт увеличения множества Р удаётся добиться того, чтобы вообще любая формула q обладала свойством: либо Определение 3.3. Множество формул называется полным, если для любой формулы q либо Очевидно, что для любого полного непротиворечивого множества формул кандидат в «хорошие» наборы единственен (хотя и он теоретически может оказаться «нехорошим»). Соответственно, достаточно доказать следующее утверждение. Лемма 3.4.Для любого непротиворечивого множества формул Р существует непротиворечивое полное множество формул Доказательство. Пусть формула q такова, что ни q, ни Пусть это не так: оба эти множества противоречивы. Тогда, согласно пункту б доказательства леммы 3.2., из противоречивости множества Соответственно, можно выбрать из двух формул ту, добавление которой не делает множество противоречивым, и добавить её. В случае, когда множество всех формул счётно, можно просто добавлять формулы по одной, и в пределе получить искомое множество К сожалению, в дальнейшем определённо придётся рассматривать несчётные множества формул, поэтому лемму необходимо доказать и для них. С этой целью придётся обратиться к широко известной лемме Цорна, которая в действительности является наиболее употребительной в алгебре равносильной переформулировкой аксиомы выбора. Коротко говоря, это замечательное утверждение состоит в следующем. Определение 3.4.Частично-упорядоченное множество Аксиома (лемма Цорна).В индуктивном частично-упорядоченном множестве обязательно есть максимальный элемент. Замечание.В рассматриваемом случае (как и во многих других) множество Т есть множество (не всех) подмножеств некоторого множества. Конкретно, в нашем случае Т есть множество непротиворечивых подмножеств множества L всех формул. Частичный порядок в данном случае (тоже – стандартно) есть просто отношение Итак, пусть цепь Итак, множество непротиворечивых множеств формул индуктивно. Значит в нём есть максимальный элемент QED Итак, показано, что любое непротиворечивое множество формул Р содержится в некотором непротиворечивом полном множестве Лемма 3.5.Для любой формулы q равносильны условия: (1) (2) Доказательствоснова проводится индукцией по множеству формул с использованием выводимостей, приведённых в доказательстве леммы 3.2. Пусть, например, Случай 1. Случай 2. Остальные два случая и все случаи, касающиеся других логических связок, рассматриваются как случай 1 (почему?). QED В частности доказано, что QED Как из теоремы 3.3. следует теорема о полноте исчисления высказываний? Пусть QED
В качестве бонуса к этому доказательству (недоступного исходя из первого доказательства) можно указать следующий простой, но крайне важный результат. Теорема 3.6.(Теорема о компактности для исчисления высказываний) Пусть P – множество формул, всякое конечное подмножество которого совместно. Тогда и само множество Р совместно. Доказательство.Пусть Р несовместно. Тогда Р противоречиво. Тогда из множества Р можно вывести формулу О. Обозначим символом QED Замечание.Основная идея доказательства состоит в том, что для выводимости и непротиворечивости теорема компактности тривиальна. И если уж непротиворечивость равносильна совместности, то…
Общая картина Что означает теорема о полноте исчисления высказываний? На данный момент рассмотрены две теории: семантическая – состоящая из всевозможных тавтологий, и синтаксическая – состоящая из теорем исчисления высказываний. Теорема о полноте утверждает, что они совпадают, то есть в данном случае мир познаваем J. В тех случаях, когда к семантической теории удаётся подобрать синтаксического «близнеца», говорят, что эта теория аксиоматизируема. Итак: пропозициональная теория аксиоматизируема. Не будем забывать также, что в действительности была доказана более сильная теорема Оставим в стороне философский аспект и посмотрим на контекст более практично. Предположим, что рассматривается некоторая семантически заданная теория. Теоретически есть два способа превратить её из «идеального объекта» в нечто осязаемое (то есть – по данной формуле определить, принадлежит ли она рассматриваемой теории). Во-первых, она может оказаться разрешимой. В этом случае (теоретически!) вопрос о принадлежности ей любой формулы решается однозначно и за конечное время, поэтому можно сказать, что мы знаем в этой теории всё. Лучшего, кажется, и желать не стоит J. В действительности (ложка дёгтя в бочке мёда) упомянутое «конечное время» может оказаться слишком велико, чтобы практически пользоваться разрешающим алгоритмом. Во-вторых, она может оказаться аксиоматизируемой. В этом случае, рассматриваемую формулу можно попробовать доказать (без гарантии успеха), вооружившись знанием того, что искомое доказательство существует. Эта способ со стороны кажется «менее надёжным», однако (по странной случайности J) обычно проще придумать доказательство формулы, чем дождаться окончания работы над ней разрешающей процедуры. Именно поэтому, например, элементарная геометрия (которая, вообще-то разрешима) практически всегда рассматривается как аксиоматизируемая (точнее – аксиоматизированная!) теория. Ну и остаётся вопрос: а бывает ли так, чтобы теория была недоступна обработке обоими этими инструментами? Это – тот самый, вопрос который (неожиданно, разочаровывающее и одновременно – стимулирующее к новым интеллектуальным подвигам J) решается отрицательно теоремой Гёделя о неполноте арифметики.
Исчисление секвенций Мотивировка Если внимательно присмотреться, то рассмотрения §2 наводят на мысль о небольшом противоречии, присущем исчислению высказываний. Доказательства строятся с начала, от аксиом. Это неудивительно: естественное правило вывода modus ponens – однонаправлено и необратимо. Тем не менее, с практической точки зрения это неудобно. Доказательство приходится строить буквально «вслепую», штамповать теоремы одну за другой в надежде, что «кривая» выведет куда надо. Впрочем, иная картина заставила бы усомниться в адекватности рассматриваемой модели мыслительной деятельности J. При этом очевидно, что строить доказательства удобнее с конца, постепенно упрощая доказываемую теорему. Практически это и случилось в первом доказательстве. Более последовательно эта точка зрения реализована в так называемом исчислении секвенций. Говорят, что исчисление секвенций – исчисление генценовского типа (от фамилии Герхарда Генцена, который начал их изучать), в отличие от исчисления высказываний, которое относят к исчислениям гильбертовского типа (от фамилии более известного парня J). Один из естественных способов поиска доказательства – проверка обсуждаемой теоремы на состоятельность, Иначе – поиск контрпримера. Предположим, дана формула q. Как построить контрпример к ней? Для начала следует проанализировать её структуру. Предположим, что формула имеет вид

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. . В одну сторону это утверждение даже доказано (теорема 2.2), поэтому достаточно проверить импликации
. В одну сторону это утверждение даже доказано (теорема 2.2), поэтому достаточно проверить импликации  и
и  (*).
(*). , q – формула. Положим
, q – формула. Положим  .
. . Тогда для любых
. Тогда для любых 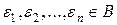 если
если  есть значение, которое формула q, принимает, если значения переменных
есть значение, которое формула q, принимает, если значения переменных  суть
суть  , то
, то  .
. обязательно что-нибудь выводится: иногда это, как в доказываемой теореме, формула q, а иногда, когда это невозможно, – из них выводится «вместо неё» формула
обязательно что-нибудь выводится: иногда это, как в доказываемой теореме, формула q, а иногда, когда это невозможно, – из них выводится «вместо неё» формула  ). С другой стороны, это свойство если и переносится на случай, когда в левой части стоят более сложные формулы, то с некоторыми сложностями.
). С другой стороны, это свойство если и переносится на случай, когда в левой части стоят более сложные формулы, то с некоторыми сложностями. ,
, 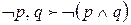 ,
,  ,
,  ,
, 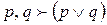 ,
,  ,
,  ,
, 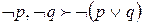 ,
,  ,
,  ,
, 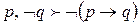 ,
, 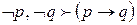 ,
, 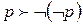 ,
, 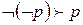 . Для примера приведём некоторые выводы.
. Для примера приведём некоторые выводы.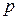 – посылка;
– посылка; – аксиома (А5);
– аксиома (А5); – правило МР;
– правило МР; – посылка;
– посылка;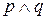 – правило МР.
– правило МР. . Докажем это правило.
. Докажем это правило. , то
, то 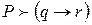 . Пусть
. Пусть  – соответствующий вывод. Аналогично, если
– соответствующий вывод. Аналогично, если  , то
, то  , соответствующий вывод обозначим
, соответствующий вывод обозначим  . Напишем второй вывод после первого и добавим к получившемуся выводу ещё три строки:
. Напишем второй вывод после первого и добавим к получившемуся выводу ещё три строки: – Аксиома (А10);
– Аксиома (А10);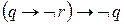 – правило МР;
– правило МР;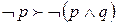 , которая заменяет две указанные выводимости (какие?). Согласно предыдущему пункту, для этого достаточно вывести из посылок
, которая заменяет две указанные выводимости (какие?). Согласно предыдущему пункту, для этого достаточно вывести из посылок 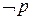 и
и  . В качестве таковых подойдут, например, формулы p и
. В качестве таковых подойдут, например, формулы p и  – аксиома (А3);
– аксиома (А3); . Согласно лемме о дедукции, если
. Согласно лемме о дедукции, если 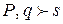 , то
, то 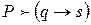 . Пусть
. Пусть 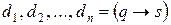 – соответствующий вывод. Аналогично, если
– соответствующий вывод. Аналогично, если 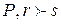 , то
, то  , соответствующий вывод обозначим
, соответствующий вывод обозначим 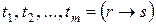 . Напишем второй вывод после первого и добавим к получившемуся выводу ещё пять строк:
. Напишем второй вывод после первого и добавим к получившемуся выводу ещё пять строк: – Аксиома (А8);
– Аксиома (А8); – правило МР;
– правило МР; – правило МР;
– правило МР;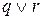 – посылка;
– посылка; – правило МР.
– правило МР.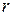
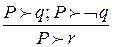 , то есть из противоречивых посылок можно вывести всё что угодно. Действительно, добавим к двум соответствующим выводам три строки:
, то есть из противоречивых посылок можно вывести всё что угодно. Действительно, добавим к двум соответствующим выводам три строки: – аксиома (А9);
– аксиома (А9); – правило МР;
– правило МР; две противоречащие друг другу формулы (или доказать их выводимости). Заметим, что всё что угодно можно вывести из двух других троек:
две противоречащие друг другу формулы (или доказать их выводимости). Заметим, что всё что угодно можно вывести из двух других троек:  , а во втором –
, а во втором –  );
); является несовместным. Кроме того, несовместность множества формул можно записать коротко и элегантно:
является несовместным. Кроме того, несовместность множества формул можно записать коротко и элегантно: 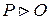 , поскольку О – одна из формул, которые никогда не бывают истинными (то есть, если все формулы семейства Р по какому-то недосмотру показались одновременно истинными, то и формула О окажется истинной, а это невозможно).
, поскольку О – одна из формул, которые никогда не бывают истинными (то есть, если все формулы семейства Р по какому-то недосмотру показались одновременно истинными, то и формула О окажется истинной, а это невозможно). и
и  . Это – синтаксическое определение противоречивости. Как уже отмечалось, из противоречивого множества формул можно в три строчки вывести всё что угодно. Например, формулу О:
. Это – синтаксическое определение противоречивости. Как уже отмечалось, из противоречивого множества формул можно в три строчки вывести всё что угодно. Например, формулу О: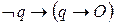 (аксиома (А9));
(аксиома (А9)); (МР);
(МР); . Оказывается, в исчислении высказываний семантическая противоречивость равносильна синтаксической.
. Оказывается, в исчислении высказываний семантическая противоречивость равносильна синтаксической. .
.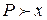 , то из предыдущего соображения ясно, что эта переменная в хорошем наборе должна быть истинна. Если же
, то из предыдущего соображения ясно, что эта переменная в хорошем наборе должна быть истинна. Если же 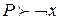 , то эта переменная должна быть ложна. Осталось:
, то эта переменная должна быть ложна. Осталось: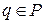 .
.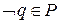 .
. , такое, что
, такое, что  .
. или
или  непротиворечиво.
непротиворечиво.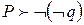 , то есть множество Р оказывается противоречивым (а это не так).
, то есть множество Р оказывается противоречивым (а это не так). называется индуктивным, если в нём любое линейно-упорядоченное подмножество (цепь) имеет верхнюю грань.
называется индуктивным, если в нём любое линейно-упорядоченное подмножество (цепь) имеет верхнюю грань. «являться подмножеством», а в качестве верхней грани цепи
«являться подмножеством», а в качестве верхней грани цепи 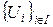 , где
, где 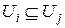 при
при  в I, берётся объединение
в I, берётся объединение  . Соответственно, проверка индуктивности множества Т есть, попросту, проверка того, что если уж
. Соответственно, проверка индуктивности множества Т есть, попросту, проверка того, что если уж 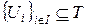 , то и
, то и 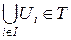 . Простыми словами: объединение цепочки непротиворечивых множеств само есть непротиворечивое множество. Искомый же «максимальный элемент» окажется, как ни удивительно, тем самым полным непротиворечивым множеством.
. Простыми словами: объединение цепочки непротиворечивых множеств само есть непротиворечивое множество. Искомый же «максимальный элемент» окажется, как ни удивительно, тем самым полным непротиворечивым множеством. . Выпишем соответствующий вывод. В него, возможно, входят и посылки. Вывод – конечное множество формул, поэтому и множество использованных посылок тоже конечно. Номером посылки назовём наименьший среди номеров множеств
. Выпишем соответствующий вывод. В него, возможно, входят и посылки. Вывод – конечное множество формул, поэтому и множество использованных посылок тоже конечно. Номером посылки назовём наименьший среди номеров множеств  , в которые эта посылка входит. Отметим среди элементов линейно-упорядоченного множества I номера всех использованных посылок. Множество отмеченных элементов конечно, поэтому найдётся максимальный отмеченный элемент I, обозначим его k. Поскольку
, в которые эта посылка входит. Отметим среди элементов линейно-упорядоченного множества I номера всех использованных посылок. Множество отмеченных элементов конечно, поэтому найдётся максимальный отмеченный элемент I, обозначим его k. Поскольку 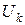 . Отсюда следует, что
. Отсюда следует, что 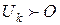 , то есть множество
, то есть множество 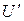 . Если множество
. Если множество  и
и  больше, чем само
больше, чем само  , который может оказаться «хорошим», определён (необязательно однозначно: при добавлении любой формулы q могло статься, что оба набора
, который может оказаться «хорошим», определён (необязательно однозначно: при добавлении любой формулы q могло статься, что оба набора 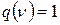 ;
; ).
).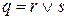 и для формул r и s утверждение уже доказано. Тогда возможны четыре случая.
и для формул r и s утверждение уже доказано. Тогда возможны четыре случая.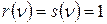 . Тогда и
. Тогда и  и
и  . Отсюда, как обычно,
. Отсюда, как обычно, 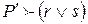 , и в этом случае для формулы q утверждение доказано.
, и в этом случае для формулы q утверждение доказано.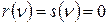 . Тогда и
. Тогда и 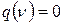 . С другой стороны, это означает, что
. С другой стороны, это означает, что 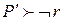 и
и  , то есть
, то есть 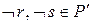 , отсюда
, отсюда  .
.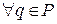
 . Тогда, очевидно,
. Тогда, очевидно,  , поскольку все наборы аргументов, на которых истинны формулы, входящие в Р, обращают q в истину, и, соответственно,
, поскольку все наборы аргументов, на которых истинны формулы, входящие в Р, обращают q в истину, и, соответственно,  , откуда, по лемме о дедукции, получаем
, откуда, по лемме о дедукции, получаем  . Вместе с аксиомой
. Вместе с аксиомой 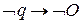 и вариантом аксиомы (А10)
и вариантом аксиомы (А10) 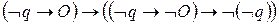 это позволяет вывести
это позволяет вывести  . Осталось воспользоваться стандартной выводимостью
. Осталось воспользоваться стандартной выводимостью 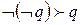 .
.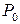 множество всех посылок, входящих в этот вывод. Тогда
множество всех посылок, входящих в этот вывод. Тогда  , т.е.
, т.е.  , из которой следует весьма важная теорема о компактности, которую, в свою очередь, можно спекулятивно переформулировать так: познаваемый мир не может быть «слишком сложно устроен», у него должны быть сравнительно простые взаимоотношения с бесконечностью. Впрочем, применительно к пропозициональной логике этот тезис выглядит странным и преждевременным, ведь соответствующая теория разрешима, то есть рассматриваемый мир, можно сказать, прост до тривиальности.
, из которой следует весьма важная теорема о компактности, которую, в свою очередь, можно спекулятивно переформулировать так: познаваемый мир не может быть «слишком сложно устроен», у него должны быть сравнительно простые взаимоотношения с бесконечностью. Впрочем, применительно к пропозициональной логике этот тезис выглядит странным и преждевременным, ведь соответствующая теория разрешима, то есть рассматриваемый мир, можно сказать, прост до тривиальности.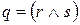 . Тогда следует поискать набор значений переменных, который делает обе формулы r и s ложными. Заметим, что эти две задачи проще исходной. Это правило можно оформить в виде дроби
. Тогда следует поискать набор значений переменных, который делает обе формулы r и s ложными. Заметим, что эти две задачи проще исходной. Это правило можно оформить в виде дроби  , которая уже встречалась в курсе. В исчислении секвенций эта дробь – одно из правил вывода.
, которая уже встречалась в курсе. В исчислении секвенций эта дробь – одно из правил вывода.