
|
|
ОСНОВНОЕ УРАВНЕНИЕ ПЕРЕДАЧИ ПО СВЕТОВОДУ
Для описания поведения электромагнитного поля в сердечнике (0 < r < a) и в оболочке (a < r < b) необходимо использовать различные функции. Исходя из физической сущности процессов, функции внутри сердечника при r = 0 должны быть конечными, а в оболочке описывать спадающее поле. Для определения наиболее важных параметров световодов (критическая частота, волновое число, скорость передачи и др.) воспользуемся основными уравнениями электродинамики – уравнениями Максвелла, которые для диэлектрических волноводов имеют следующий вид:
Уравнения Максвелла справедливы для любой системы координат. Для направляющих систем эти уравнения наиболее часто применяются в цилиндрической системе координат, ось Z которой совместим с оптической осью световода:
Для решения инженерных задач электродинамики необходимо знать продольные составляющие полей Еz и Hz. Их можно получить следующим образом. Преобразуем первое из уравнений Максвелла (8.1) к виду
Тогда, используя соотношение
где Поступая аналогично со вторым уравнением Максвелла (8.1), получим
Отсюда следует, что продольные электромагнитные составляющие векторов Ez и Hz удовлетворяют уравнениям
где
Тогда для продольных составляющих Ez и Hz в цилиндрической системе координат получим дифференциальные уравнения второго порядка:
Допустим, что напряженность электромагнитного поля в направлении оси Z меняется по экспоненциальному закону, т. е.
Для составляющей Еz имеем Подставляя полученное выражение в уравнения (8.3), получим
Введем обозначение
где Решение уравнений (8.4) для сердечника следует выразить через цилиндрические функции первого рода – функции Бесселя, имеющие конечные значения при r = 0. Поэтому
где Аn и Вn – постоянные интегрирования. Воспользовавшись уравнениями (8.2), рассмотрим связь между поперечными и продольными компонентами поля. В частности, для составляющей Еr имеем
Возьмем производную от второго выражения по
Учитывая, что Тогда Подставим данное выражение в уравнение для Еr:
или
Окончательно получим Аналогично можно установить связь между продольными и другими поперечными компонентами поля:
Воспользовавшись уравнениями (8.5) возьмем соответствующие производные:
Тогда выражения для поперечных составляющих электрического и магнитного полей в сердечнике световода, с учетом, что
Для оболочки имеем аналогичную систему уравнений:
где Для решения данных уравнений, исходя из условия, что при
где Сn, Dn – постоянные интегрирования. Возьмем соответствующие производные
Тогда для поперечных составляющих поля в оболочке получим следующие выражения:
Постоянные интегрирования Аn, Вn, Сn, Dn могут быть определены на основании граничных условий. Используем условия равенства тангенциальных составляющих напряженностей электрических и магнитных полей на поверхности раздела сердечник–оболочка (при r = а):
Найдя постоянные интегрирования, подставив их в уравнения (8.6) и (8.7), и после соответствующих преобразований получим следующее трансцендентное уравнение:
Полученные уравнения дают возможность определить неизвестные постоянные и найти структуру поля в сердечнике и оболочке волоконного световода. В общем случае уравнения имеют ряд решений, каждому из которых соответствует определенная структура поля, называемая типом волны или модой.
Контрольные вопросы 1. Объясните физический смысл уравнений Максвелла. 2. Что такое поперечное волновое число сердечника? 3. Что такое поперечное волновое число оболочки? 4. Почему электромагнитное поле в световоде описывается различными функциями? 5. В чем смысл основного уравнения передачи по световоду?

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рассмотрим волоконный световод без потерь двухслойной конструкции (рис. 17).
Рассмотрим волоконный световод без потерь двухслойной конструкции (рис. 17). (8.1)
(8.1) (8.2)
(8.2) .
. , а также учитывая, что divH = 0, получим
, а также учитывая, что divH = 0, получим ,
,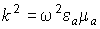 – волновое число световода.
– волновое число световода. .
.
 – оператор Лапласа:
– оператор Лапласа: .
. (8.3)
(8.3) , где А – любая составляющая векторов Е или Н;
, где А – любая составляющая векторов Е или Н;  j
j 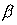 – коэффициент распространения. Тогда первая и вторая производные
– коэффициент распространения. Тогда первая и вторая производные .
. .
.
 – поперечное волновое число световода. Тогда для сердечника световода имеем
– поперечное волновое число световода. Тогда для сердечника световода имеем (8.4)
(8.4) (без учета затухания) – поперечное волновое число сердечника; k1 – волновое число сердечника с коэффициентом преломления n1,
(без учета затухания) – поперечное волновое число сердечника; k1 – волновое число сердечника с коэффициентом преломления n1, 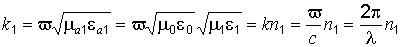 .
. (8.5)
(8.5)


 , а
, а  , то
, то  .
. , или
, или  .
. ,
, .
. .
.
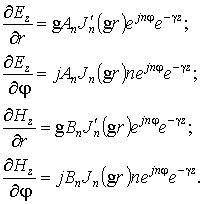
 , имеют следующий вид (множитель
, имеют следующий вид (множитель  не пишем):
не пишем): (8.6)
(8.6)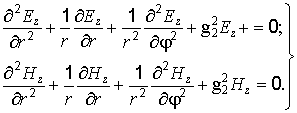
 (без учета затухания) – поперечное волновое число оболочки световода; k2 – волновое число оболочки с коэффициентом преломления n2,
(без учета затухания) – поперечное волновое число оболочки световода; k2 – волновое число оболочки с коэффициентом преломления n2,  .
.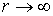 поле должно стремиться к нулю, следует использовать цилиндрические функции третьего рода – функции Ганкеля:
поле должно стремиться к нулю, следует использовать цилиндрические функции третьего рода – функции Ганкеля: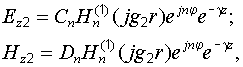

 (8.7)
(8.7)


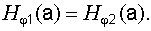

 (8.8)
(8.8)