
|
|
Свободная и несвободная точкиМатериальная точка, движение которой в пространстве не огра- ничено какими-либо связями, называется свободной. Примером свободной материальной точки может служить искусственный спутник Земли в околоземном пространстве или летящий самолет. Их перемещение в пространстве ничем не ограничено, поэтому лет- чик на спортивном самолете способен проделывать различные сложные фигуры высшего пилотажа. Задачи динамики сводятся к двум основным: 1) задается закон движения точки, требуется определить дейст- вующую на нее силу или систему сил (первая задача динамики); 2) задается система сил, действующая на точку, требуется оп- ределить закон движения (вторая задача динамики).
Материальная точка, свобода перемещения которой ограничена наложенными связями, называется несвободной. Примером несво- бодной материальной точки может служить движущийся по рель- сам трамвай, если пренебречь его формой и размерами. Для несво- бодной материальной точки все внешние силы необходимо делить на две категории: активные (движущие) силы и реакции связи (пас- сивные силы). В связи с этим первая задача динамики несвободной точки сводится к определению реакций связей, если заданы законы движения точки и действующие на нее активные силы. Вторая за- дача динамики сводится к тому, чтобы, зная действующие на точку активные силы, определить, во-первых, закон движения точки и, во- вторых, реакции связей. Если несвободную материальную точку освободить от связей и заменить связи их реакциями, то движение точки можно рассматри- вать как свободное, а основному закону динамики придать такой вид:
где Fk – активные силы;
m – масса точки;
Силы инерции
Fин .
Рис. 9.3. Сила инерции
Сила инерции в действительности не приложена к получившей ускорение материальной точке, а действует на точку или тело, ко- торое сообщает ускорение этой точке. Поясним это несколькими примерами.
инерции Fин , численно равная ma , противодействующая выходу груза из состояния инерции (рис. 9.4, в). Нить может оборваться и в том случае, если толкнуть в горизонтальном направлении подве- шенный груз, заставив его раскачиваться на нити (рис. 9.4, г).
(нормальное ускорение) и aτ (каса- тельное ускорение). Поэтому при криволинейном движении мате-
Нормальная (иначе центробежная) сила инерции
Fин :
И касательная (иначе тангенциальная) сила инерции
Fин.n Fин.τ
ρ
ин.n
а б в г Рис. 9.4. К анализу дейсвия сил инерции
Рис. 9.5. Векторы ускорений и сил инерции Принцип Даламбера Силы инерции широко используются при расчетах и решении технических задач, причем использование сил инерции позволяет решения многих задач, в которых рассматривается движение несво- бодной материальной точки, свести к знакомым нам уравнениям статики:
Условно прикладывая силу инерции Fин к движущейся матери-
Fk , реакции свя- зей Rk и сила инерции Fин образуют уравновешенную систему (принцип Даламбера). Решение задач динамики с помощью принципа Даламбера ино- гда называют методом кинетостатики. ГЛАВА 10. РАБОТА И МОЩНОСТЬ 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 Обе задачи динамики решаются с помощью основного закона динамики, записанного в форме F ma или F ma .
Обе задачи динамики решаются с помощью основного закона динамики, записанного в форме F ma или F ma . ,
,
 Rk – реакции связей;
Rk – реакции связей; a – ускорение точки, полученное в результате действия внеш- них сил (активных и пассивных).
a – ускорение точки, полученное в результате действия внеш- них сил (активных и пассивных). Сила, численно равная произведению массы материальной точки на приобретенное ею ускорение и направленная в сторону, противо- положную ускорению, называется силой инерции (рис. 9.3):
Сила, численно равная произведению массы материальной точки на приобретенное ею ускорение и направленная в сторону, противо- положную ускорению, называется силой инерции (рис. 9.3):
 Тяжелый груз, масса которого m, висит на непрочной, но спо- собной выдержать натяжение R = G нити (рис. 9.4, а). Если теперь резко потянуть нить вертикально вверх, то она может оборваться (рис. 9.4, б). На нить начинает действовать дополнительная сила
Тяжелый груз, масса которого m, висит на непрочной, но спо- собной выдержать натяжение R = G нити (рис. 9.4, а). Если теперь резко потянуть нить вертикально вверх, то она может оборваться (рис. 9.4, б). На нить начинает действовать дополнительная сила риальной точки возникают две составляющие силы инерции
риальной точки возникают две составляющие силы инерции
 Fин.n
Fин.n
 an
an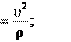





 альной точке, можем считать, что активные силы
альной точке, можем считать, что активные силы