|
|
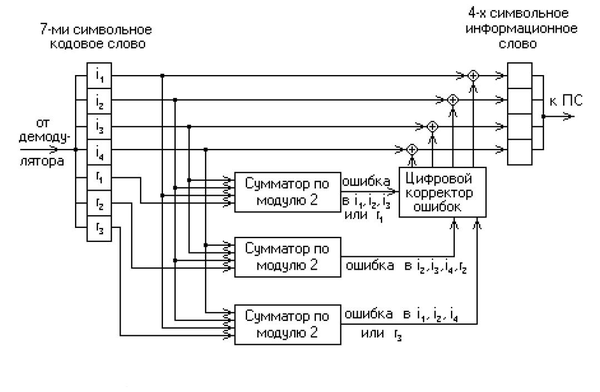
Систематические групповые кодыСистематические коды образуют наиболее обширную группу (n, k)- разделимых кодов. Особенностью этих кодов является то, что проверочные (корректирующие) символы образуются с помощью линейных операций над информационными. Кроме того, любая разрешённая кодовая комбинация может быть получена в результате линейной операции над набором к линейно независимых кодовых комбинаций. В частности, суммирование по модулю 2 двух и более разрешённых комбинаций также дает разрешённую кодовую комбинацию. Поскольку теоретической основой получения таких комбинаций является математический аппарат линейной алгебры, то коды и называют линейными, а учитывая, что проверочные символы формируются по определённой системе (правилам), блочные равномерные разделимые линейные коды получили название систематических. Использование аппарата линейной алгебры, в которой важное значение имеет понятие "группа", породило и другое название этих кодов - групповые. Эти коды получили наибольшее применение в системах передачи дискретной информации. Коды Хэмминга Построение кодов Хемминга основано на принципе проверки на четность числа единичных символов: к последовательности добавляется элемент такой, чтобы число единичных символов в получившейся последовательности было четным.
знак Получение кодового слова выглядит следующим образом:
На вход декодера поступает кодовое слово
Получение синдрома выглядит следующим образом:
Кодовые слова
Синдром
Циклические коды. Представление двоичного кода в виде полинома Циклический код — линейный код, обладающий свойством цикличности, то есть каждая циклическая перестановка кодового слова также является кодовым словом. Используется для преобразования информации для защиты её от ошибок Широкое распространение на практике получил класс линейных кодов, которые называются циклическими. Данное название происходит от основного свойства этих кодов: если некоторая кодовая комбинация принадлежит циклическому коду, то комбинация полученная циклической перестановкой исходной комбинации (циклическим сдвигом), также принадлежит данному коду. Вторым свойством всех разрешенных комбинаций циклических кодов является их делимость без остатка на некоторый выбранный полином, называемый производящим. Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на производящий полином. Эти свойства используются при построении кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
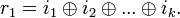 знак
знак  здесь означает сложение по модулю 2
здесь означает сложение по модулю 2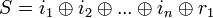 .
. 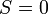 - ошибки нет,
- ошибки нет, 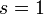 однократная ошибка. Такой код называется
однократная ошибка. Такой код называется  или
или 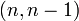 . Первое число - количество элементов последовательности, второе - количество информационных символов. Для каждого числа проверочных символов
. Первое число - количество элементов последовательности, второе - количество информационных символов. Для каждого числа проверочных символов 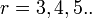 существует классический код Хемминга с маркировкой
существует классический код Хемминга с маркировкой 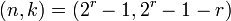 т.е. -
т.е. -  . При иных значениях k получается так называемый усеченных код, например международный телеграфный код МТК-2, у которого
. При иных значениях k получается так называемый усеченных код, например международный телеграфный код МТК-2, у которого 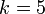 . Для него необходим код Хемминга
. Для него необходим код Хемминга 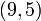 , который является усеченным от классического
, который является усеченным от классического 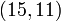 . Для Примера рассмотрим классический код Хемминга
. Для Примера рассмотрим классический код Хемминга  . Сгруппируем проверочные символы следующим образом:
. Сгруппируем проверочные символы следующим образом:



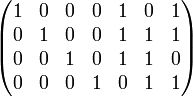 =
= 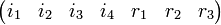
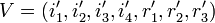 где штрихом помечены символы, которые могут исказиться в результате помехи. В декодере в режиме исправления ошибок строится последовательность синдромов:
где штрихом помечены символы, которые могут исказиться в результате помехи. В декодере в режиме исправления ошибок строится последовательность синдромов:
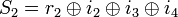
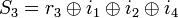
 называется синдромом последовательности.
называется синдромом последовательности. =
= 
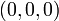 указывает на то, что в последовательности нет искажений. Каждому ненулевому синдрому соответствует определенная конфигурация ошибок, которая исправляется на этапе декодирования. Для кода
указывает на то, что в последовательности нет искажений. Каждому ненулевому синдрому соответствует определенная конфигурация ошибок, которая исправляется на этапе декодирования. Для кода