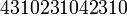|
|
Классификация помехоустойчивых кодовВ непрерывных кодах передаваемая информационная последовательность не разделяется на блоки. Избыточные элементы размещаются в определенном порядке между информационными. Равномерные блочные коды делятся на разделимые и неразделимые. В разделимых кодах элементы информационной и проверочной частей кодовой комбинации всегда стоят на определенных местах. В неразделимых кодах деление на информационные и проверочные разряды отсутствует. Разделимые коды, в свою очередь, делятся на систематические (линейные) и несистематические (нелинейные). Систематическими кодами называются блочные разделимые (n,k)-коды, в которых проверочные элементы представляют собой линейные комбинации информационных, несистематические коды таким свойством не обладают. Помехоустойчивое кодирование предполагает введение в передаваемое сообщение, наряду с информационными, так называемых проверочных разрядов, формируемых в устройствах защиты от ошибок (кодерах-на передающем конце, декодерах — на приемном). Избыточность позволяет отличить разрешенную и запрещенную (искаженную за счет ошибок) комбинации при приеме, иначе одна разрешенная комбинация переходила бы в другую. Помехоустойчивый код характеризуется тройкой чисел (n, k, d0), где n— общее число разрядов в передаваемом сообщении, включая проверочные (г), k=n-r - число информационных разрядов, d0— минимальное кодовое расстояние между разрешенными кодовыми комбинациями, определяемое как минимальное число различающихся бит в этих комбинациях. Число обнаруживаемых (tj и (или) исправляемых (t ) ошибок (разрядов) связано с параметром d0 соотношениями Иногда используются дополнительные показатели избыточности, производные от приведенных выше характеристик n, k:R = r/n- относительная избыточность, v = k / n - относительная скорость передачи. Существующие помехоустойчивые коды можно разделить на ряд групп, только часть из которых используется для обнаружения ошибок в передаваемых по сети пакетах. В группе систематических (линейных) кодов общим свойством является то, что любая разрешенная комбинация может быть получена в результате линейных операций над линейно-независимыми векторами. Это способствует упрощению аппаратной и программной реализации данных кодов, повышает скорость выполнения необходимых операций.
Рис. 1.1. Классификация помехоустойчивых кодов Простейшими систематическими кодами являются биты четности/нечетности. Они не позволяют обнаружить ошибки четной кратности (т.е. ошибки одновременно в двух, четырех и т.д. битах) и поэтому используются при невысоких требованиях к верности принимаемых данных (или при малой вероятности ошибок в линии передачи). Примером может служить бит Parity (соответствие) в установках режимов работы последовательного порта с помощью команды MODE (MS DOS). Несмотря на ограниченные возможности обнаружения ошибок, биты четности/нечетности имеют большое значение в теории помехоустойчивого кодирования. Одни иг первых математически обоснованных и практически использовании? помехоустойчивых кодов - коды Хэмминга представляют собой простс совокупность перекрестных проверок на четность/нечетность. Циклические коды могут рассматриваться как обобщенные проверки на четность/ нечетность Клод Шеннон сформулировал теорему для случая передачи дискретной информации по каналу связи с помехами, утверждающую, что вероятность ошибочного декодирования принимаемых сигналов может быть обеспечена сколь угодно малой путем выбора соответствующего способа кодирования сигналов. В теореме Шеннона не говорится о том, как нужно строить помехоустойчивые коды. Однако в ней указывается на принципиальную возможность кодирования, при котором может быть обеспечена сколь угодно высокая верность передачи. Это явилось стимулом к разработке помехоустойчивых кодов. Помехоустойчивость кодирования обеспечивается за счет введения избыточности в кодовые комбинации, т.е. за счет того, что не все символы в кодовых комбинациях используются для передачи информации. Все помехоустойчивые коды можно разделить на два основных класса: блочные и непрерывные (рекурентные или цепные). В блочных кодах каждому сообщению (или элементу сообщения) сопоставляется кодовая комбинация (блок) из определенного количества разрядов. Блоки кодируются и декодируются отдельно друг от друга. Блочные коды могут быть равномерными, когда длина кодовых комбинаций п постоянна, или неравномерными, когда п непостоянно. В непрерывных кодах введение избыточности в последовательность входных символов осуществляется без разбивки ее на отдельные блоки. Процессы кодирования и декодирования в непрерывных кодах имеют также непрерывный характер. Как блочные, так и непрерывные коды в зависимости от методов внесения избыточности подразделяются на разделимые и неразделимые. В разделимых кодах четко разграничена роль отдельных символов. Одни символы являются информационными, другие являются проверочными и служат для обнаружения и исправления ошибок. Разделимые блочные коды называются обычно п,k-кодами, где п – длина кодовых комбинаций, k – число информационных символов в комбинациях. Неразделимые коды не имеют четкого разделения кодовой комбинации на информационные и проверочные символы. Разделимые блочные коды делятся, в свою очередь, на несистематические и систематические. Несистематические разделимые коды строятся таким образом, что проверочные символы определяются как сумма подблоков длины l, на которые разделяется блок информационных символов. Большинство известных разделимых кодов составляют систематические коды. У этих кодов значение проверочных символов определяется в результате проведения линейных операций над определенными информационными символами. Для случая двоичных кодов каждый проверочный символ выбирается таким, чтобы его сумма по модулю два с определенными информационными символами стала равной нулю (т.е. сумма единиц была четной). Декодирование сводится к проверке на четность определенных групп символов. В результате таких проверок дается информация о наличии ошибок, а в случае необходимости – о позиции символов, где имеются ошибки.
Блоковые коды Блочный код - в информатике тип канального кодирования. Он увеличивает избыточность сообщения так, чтобы в приемнике можно было расшифровать его с минимальной (теоретически нулевой) погрешностью, при условии, что скорость передачи информации (количество передаваемой информации в битах в секунду) не превысила бы канальную производительность. Главная характеристика блочного кода состоит в том, что это – канальный код фиксированной длины (в отличие от такой схемы кодирования источника данных, как кодирование Хаффмана, и в отличие таких методов канального кодирования, как конволюционное кодирование («сверточное» кодирование) ). Обычно, система блочного кодирования получает на входе k-значное кодовое слово W, и преобразовывает его в n-значное кодовое слово C(W). Это кодовое слово и называется блоком. Блочное кодирование было главным типом кодирования, используемого в ранних системах мобильной коммуникации. Последовательность входящих информационных символов
В кодере производится преобразование каждого отдельного блока в новый блок :
Правило преобразования (функциональная зависимость, обозначенная здесь буквой Пример. Пусть алфавит языка состоит из пяти букв: а, в, л, о, с . Их кодирование в цифровую последовательность возможно по правилу:
однозначно декодирует их — если знает правило кодирования. Понятно, что для кодирования всего русского алфавита потребуются уже двузначные десятичные числа, т.е.
или же искажаться
Можно ли восстановить утраченную информацию? — Понятно, что ответ на этот вопрос зависит, в первую очередь, от передающих характеристик самого канала связи.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


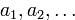 разбивается на отрезки (блоки), каждый содержащий
разбивается на отрезки (блоки), каждый содержащий  символов:
символов:
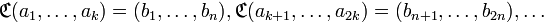
 ) каждого входящего блока не зависит от содержания других входящих блоков; получающиеся в ходе преобразваний блоки
) каждого входящего блока не зависит от содержания других входящих блоков; получающиеся в ходе преобразваний блоки 
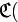 а
а  ,
,  ,
, 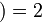 ,
, 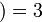 ,
, 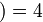 .
. 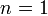 . Получатель, которому по телефону диктуют цифровые последовательности
. Получатель, которому по телефону диктуют цифровые последовательности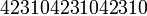 или
или 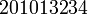
 (и отметим, на всякий случай, что кодирование по правилу
(и отметим, на всякий случай, что кодирование по правилу 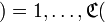 я
я 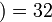 уже не будет правильным…). Пока остановимся на примере пятибуквенного алфавита чтобы показать две проблемы. Предположим, что телефонная линия подвержена помехам и какие-то сообщения могут теряться:
уже не будет правильным…). Пока остановимся на примере пятибуквенного алфавита чтобы показать две проблемы. Предположим, что телефонная линия подвержена помехам и какие-то сообщения могут теряться: