
|
|
Геометрия цилиндрических зубчатых колес и зацепленийОсновным условием, которому должны удовлетворять боковые профили зубьев зубчатых колес, является постоянство передаточного отношения передачи. Это условие обеспечивается, если выполняется требование основной теоремы зацепления: общая нормаль, проведенная в точке контакта зубьев, должна проходить через полюс зацепления «Р» независимо от положения точки контакта.
Для обеспечения высокого КПД и прочности колес профили должны иметь малые скорости скольжения при передаче движения и достаточные радиусы кривизны в точках контакта. Профили должны также допускать легкое изготовление простым инструментом независимо от числа зубьев. Из всего разнообразия профилей всем этим условиям наиболее полно отвечают боковые профили зубьев, очерченные по эвольвенте окружности. Колеса с такими профилями образуют так называемое эвольвентное зацепление, нашедшее широчайшее применение в машиностроении. Каждое эвольвентное колесо может входить в зацепление с колесами того же модуля, имеющими любое число зубьев. Эвольвентное зацепление мало чувствительно к отклонениям межосевого расстояния Эвольвентой называется кривая, которая описывается точкой В, лежащей на касательной NN к окружности, если эту касательную обкатывать без скольжения по окружности в ту или иную сторону (рис. 4.4). Касательная NN называется производящей прямой, а окружность диаметра db, по которой перекатывается эта прямая линия, – основной окружностью. Из образования эвольвенты следует, что основная окружность является геометрическим местом центров кривизны эвольвенты, поэтому нормаль к эвольвенте касается основной окружности, а радиус кривизны эвольвенты ρ в любой ее точке равен длине отрезка АВ производящей прямой NN. Следовательно, ρ = АВ = дуге АС. Угол СОВ называется эвольвентным углом профиля зуба inva (инволюта угла α). Из рис. 4.4 имеем
Зависимость (4.9) называется уравнением эвольвенты, так как угол inv(α) и радиус-векторl полностью определяют координаты точки на эвольвенте, построенной на основной окружности диаметра db. Образование простейшего зубчатого механизма представлено на рис.4.5. Возьмем передачу, в которой окружности с диаметрами dw1 и dw2 перекатывающиеся друг по другу без скольжения. Эти окружности, касающиеся друг друга в полюсе зацепления P, принято называть начальными окружностями. Если на начальных окружностях расположить последовательно чередующиеся выступы-зубья и впадины, то передача будет осуществляться при помощи боковых профилей зубьев. Боковые профили зубьев часто выполнены в виде эвольвент, образованных на основных окружностях диаметрами db1 и db2. Боковые профили зубьев представляют собой взаимоогибаемые кривые, которые передают движение при наличии качения со скольжением. Точка Р (мгновенный центр относительного вращения), принадлежащая неподвижной плоскости, называется полюсом зацепления. Полюс зацепления совпадает с точкой пересечения межосевой линии О1О2 с общей нормалью NN к двум сопряженным профилям. Из условия образования эвольвенты следует, что АК – нормаль к эвольвенте первого колеса и одновременно радиус кривизны в этой точке, а ВК – соответственно нормаль и радиус кривизны второй эвольвенты в точке касания боковых профилей зубьев К. Поскольку прямая АВ является касательной одновременно к обеим основным окружностям, положение ее неизменно, поэтому пересечение линии АВ с линией центров О1О2 находится в полюсе зацепления Р, что соответствует основной теореме зацепления. Расстояние между осями колес по межосевой линии называется межосевым расстояниеми обозначаетсяaw.
Рис. 4.5
Геометрическое место точек контакта зубьев на неподвижной плоскости называется линией зацепления. В эвольвентной передаче линия зацепления совпадает с производящей прямой АВ. Отрезок ab называется активной линией зацепления. Точки a и b находятся на пересечении линии зацепления АВ с окружностями вершин зубьев. Угол aω между линией зацепления и прямой, перпендикулярной к межосевой линии, называется углом зацепления. Расстояние между одноименными профилями соседних зубьев, измеренное по дуге концентрической окружности зубчатого колеса называется окружным шагом р. Шаг может быть измерен по любой окружности. Отношение шага к числу π называется модулем зацепления
Модуль является основным параметром зубчатого зацепления, через него выражаются все размеры зубчатых колес и передачи. Модули стандартизованы в диапазоне 0,05-100 мм по ГОСТ 9563-80. Настройка инструмента при изготовлении колес производится по делительной окружности. Окружность, расположенная в пределах высоты зуба зубчатого колеса, шаг по которой соответствует стандартному значению модуля, называется делительной окружностью. Диаметр делительной окружности равен произведению модуля колеса на число зубьев z.
Окружность диаметра da, ограничивающая вершины зубьев, называется окружностью вершин зубьев; окружность диаметра df, ограничивающая впадины зубьев – окружностью впадин. Зуб колеса условно делится на головку высотой ha и ножку высотой hf. В нормальных зубчатых колесах ha=m и hf =1,25m, следовательно, высота зуба h=2,25m. Диаметр окружности вершин зубьев
Диаметр окружности впадин зубьев
Радиальный зазор (расстояние между окружностью вершин зубьев одного колеса и окружностью впадин сопряженного колеса)
Учитывая, что передаточное отношение от первого колеса ко второму получаем, что в зубчатой передаче:
Отношение числа зубьев ведомого зубчатого колеса к числу зубьев ведущего колеса (шестерни) называется передаточным числом и согласно ГОСТ обозначается буквой «u». В понижающих зубчатых передачах передаточные отношения и передаточные числа совпадают. Центральный угол концентрической окружности, равный 2π/z или 3600/z, называется шаговым угловым зубьев τ. Угол поворота зубчатого колеса передачи от положения входа зуба в зацепление до положения выхода из зацепления называется углом перекрытия φα, а отношение угла перекрытия к угловому шагу – коэффициентом перекрытия εα:
При εα=1 в зацеплении постоянно находится одна пара зубьев. При εα=2 в зацеплении постоянно находится две пары зубьев. Коэффициент перекрытия не может быть меньше 1.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рис. 4.4
Рис. 4.4
 (4.106)
(4.106)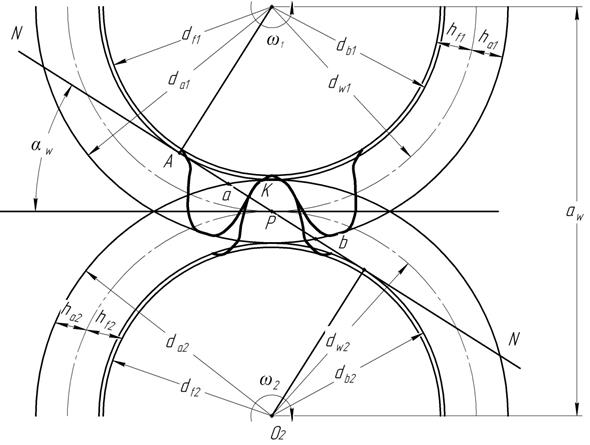
 (4.107)
(4.107) (4.108)
(4.108) (4.109)
(4.109) (4.110)
(4.110) (4.111)
(4.111) ,
, (4.112)
(4.112) (4.113)
(4.113)