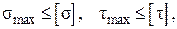|
|
Метод сечений. НапряжениеГЛАВА 2. ОСНОВЫ РАСЧЕТОВ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ Задачи и методы расчета Различные конструкции, детали и машины помимо других качеств должны обладать способностью сопротивляться разрушению под действием приложенных к ним внешних сил. Изложение методов расчёта элементов конструкций на прочность составляет первую задачу курса сопротивления материалов. Кроме этого, во многих случаях при решении конкретных инженерных задач приходится определять деформации, т. е. изменения формы и размеров элементов конструкций, которые возникают при действии нагрузок. Как известно, абсолютно твёрдых, т. е. недеформируемых, тел в природе не существует. Небольшие деформации не оказывают заметного влияния на законы равновесия и движения тела, вследствие чего в курсах теоретической механики и теории механизмов и машин ими пренебрегают. Однако без учёта деформаций невозможно решить важнейшую практическую задачу о том, при каких условиях может произойти разрушение конструкции. Кроме этого, величину деформации во многих случаях приходится ограничивать, так как в противном случае нормальная эксплуатация конструкций может оказаться невозможной. Способность элементов конструкции сопротивляться деформации под действием внешних сил называется жёсткостью. Таким образом, изложение методов расчёта конструкций на жёсткость составляет вторую задачу курса сопротивления материалов. Третья задача курса связана с изучением устойчивости форм равновесия деформирующихся тел. Под устойчивостью понимают способность элемента сопротивляться возникновению больших отклонений от невозмущенного равновесия при малых возмущающих воздействиях, т. е. при малом изменении нагрузки. Состояние устойчиво, если малому изменению нагрузки соответствует малое изменение деформации. И наоборот, равновесие будет неустойчиво, если небольшой рост нагрузки сопровождается неограниченным ростом деформаций. Примером неустойчивого равновесия является осевое сжатие тонкого стержня. Геометрическая форма элементов конструкций и деталей может быть весьма сложной. Учёт всех геометрических особенностей детали при расчёте часто бывает невозможным либо нецелесообразным. На практике для оценки прочности вводят упрощение в геометрическую форму и представляют деталь в виде стержня, пластинки, оболочки или массива. Стержнем или брусом называют тело, поперечные размеры которого малы по сравнению с его длиной. Стержень может иметь постоянное или переменное сечение. В дальнейшем в основном будем рассматривать стержни с прямолинейной осью. Пластиной называют тело, ограниченное двумя плоскими поверхностями, имеющее малую толщину по сравнению с радиусом или длиной. Оболочка – тело, ограниченное двумя неплоскими поверхностями, имеющее малую толщину по сравнению с радиусом кривизны и длиной (например, тонкостенный цилиндр). Массивом будем называть модель, три размера которой соизмеримы (например, зуб зубчатого колеса).
Допущения, принимаемые при расчётах на прочность Для упрощения решения задач в курсе сопротивления материалов принимаются некоторые упрощающие допущения относительно свойств материала, нагрузок и характера взаимодействия деталей и внешних сил, которые вносят в результат решения незначительные погрешности, но при этом существенно облегчают и упрощают само решение. 1. Материал имеет сплошное (непрерывное) строение.Это допущение приемлемо для большинства машиностроительных материалов, так как они имеют настолько мелкозернистую структуру, что можно считать их строение сплошным. 2. Материал детали однороден,т. е. обладает во всех точках одинаковыми свойствами. Все металлы и сплавы обладают высокой однородностью. Менее однородны дерево, бетон, пластические массы с наполнителем. 3. Материал считается изотропным,т. е. обладающим одинаковыми свойствами во всех направлениях. У материалов с мелкозернистой структурой кристаллы расположены хаотично и свойства в разных направлениях выравниваются, поэтому эти материалы практически изотропны. 4. В теле до приложения внешних нагрузок отсутствуют внутренние усилия.В дальнейшем под внутренними усилиями будем понимать внутренние силы упругости, которые сопротивляются разрушению и деформации, не принимая во внимание молекулярные силы, которые имеются в ненагруженном теле. 5. Результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, приложенных к телу последовательно в произвольном порядке.Под результатом воздействия в зависимости от конкретной задачи будем понимать деформации, внутренние усилия или перемещения отдельных точек. 6. Принцип Сен-Венана. В точках тела, достаточно удаленных от мест приложения нагрузок, внутренние силы весьма мало зависят от конкретного способа приложения этих нагрузок.Этот принцип позволяет производить замену одной системы сил другой, ей эквивалентной. В частности, распределённую нагрузку мы будем заменять сосредоточенной силой, модуль которой равен равнодействующей распределённой нагрузке.
Классификация внешних нагрузок Нагрузки, действующие на части машин и сооружений, представляют собой силы или пары сил (моменты), которые могут рассматриваться как сосредоточенные и распределённые. Следует отметить, что в природе сосредоточенных сил не бывает, так как через точку невозможно передать даже незначительное усилие. Все реальные силы распределены по некоторой длине, площади либо объёму. Однако для определения внутренних усилий, возникающих на некотором расстоянии от площади передачи давления, на основании принципа Сен-Венана распределённую нагрузку можно заменить сосредоточенной равнодействующей, что упростит расчёт. Сосредоточенные нагрузки выражаются в ньютонах (Н), килоньютонах (кН), меганьютонах(МН). Распределенные нагрузки выражаются в единицах силы, отнесённых к единице длины, либо к единице площади, либо к единице объёма. Равномерно распределённая нагрузка по длине (погонная нагрузка) обозначается её интенсивностью q и выражается в ньютонах на метр (Н/м), распределённая нагрузка по площади – в ньютонах на квадратный метр (Н/м2). И сосредоточенные и распределённые нагрузки могут быть статическими и динамическими. Статическими называются нагрузки, которые изменяют свою величину, или точку приложения, или направление с очень небольшой скоростью, поэтому возникающими при этом ускорениями можно пренебречь. При действии таких нагрузок колебания сооружений и их частей пренебрежимо малы. Динамическими называют нагрузки, изменяющие хотя бы один из трёх параметров, определяющих силу, как вектор, во времени с большой скоростью. Действие таких нагрузок приводит к возникновению колебаний сооружений. При колебании масс, вследствие изменения скорости, возникают силы инерции, пропорциональные колеблющимся массам и ускорениям. Эти силы могут во много раз превосходить те же нагрузки, приложенные статически. К динамическим также относятся нагрузки, периодически изменяющиеся во времени. Разделение нагрузок на статические и динамические связано с тем, что материалы различно сопротивляются этим видам нагрузок.
Основные виды деформаций Деформации элементов сооружений и деталей машин, вызванные внешними силами, могут быть очень сложными. Однако эти сложные виды деформаций всегда можно представить состоящими из небольшого числа основных видов деформаций. Основными видами деформаций элементов конструкций и деталей машин, изучаемых в курсе сопротивления материалов, являются: · растяжение (рис. 2.1); · сжатие (рис. 2.2); · сдвиг (срез) (рис. 2.3); · кручение (рис. 2.4); · изгиб (рис. 2.5).
Примерами сложных деформаций могут служить одновременные растяжения и изгиб или одновременные изгиб и кручение. В последующих главах будут рассмотрены перечисленные виды деформаций и разобраны методы определения величин напряжений и деформаций.
Метод сечений. Напряжение Внешние силы, действующие на тело, вызывают появление в нём внутренних сил упругости. Если внешние силы деформируют тело, то внутренние силы сопротивляются их воздействию и стремятся сохранить первоначальную форму и объём тела. При решении задач сопротивления материалов, связанных с расчётом на прочность и жёсткость элементов конструкций, необходимо уметь определять внутренние силы и деформации, возникающие в этих элементах. При определении внутренних сил в каком-либо сечении тела используют метод сечений. Это универсальный метод, который можно использовать при любом виде деформации, рассмотренном выше. Суть этого метода заключается в следующем. Рассмотрим тело, находящееся в состоянии равновесия под действием четырёх сил Величина равнодействующей внутренних усилий определяется из условия равновесия оставшейся части тела при помощи уравнений статики.
Метод сечений позволяет определить только сумму внутренних сил, действующих в интересующем нас сечении. Сумма этих сил может приводиться к одной силе, к паре сил или в общем случае – к силе и паре сил. Закон распределения внутренних усилий по сечению, как правило, неизвестен. Для решения этого вопроса необходимо знать в каждом конкретном случае, как деформируется данное тело под действием внешних сил. Таким образом, в поперечном сечении нагруженного внешними силами тела действуют непрерывно распределённые усилия, интенсивность которых может быть различной в разных точках сечения и в разном направлении. Если в сечении выделить бесконечно малую площадку ∆A и обозначить равнодействующую внутренних сил, действующих на эту площадку ∆R, то отношение силы ∆R к величине выделенной площадки ∆A даст среднее напряжение на этой площадке:
Таким образом, чтобы получить истинное напряжение или просто напряжение в данной точке, необходимо уменьшить до бесконечности размеры площадки:
Упрощенно можно сказать, что напряжением называется внутренняя сила, приходящаяся на единицу площади в данной точке данного сечения. Напряжение выражают в ньютонах на квадратный метр. Эта величина называется паскаль: Па = Н/м2. В технике часто применяют единицу измерения напряжения, которая носит название мегапаскаль. Один мегапаскаль равен миллиону паскалей: 106 Па = МПа. Полное напряжение р можно разложить на две составляющие: нормальную к плоскости сечения, она обозначается σ и называется нормальным напряжением; вторая составляющая лежит в плоскости сечения, она обозначается τ и называется касательным напряжением (рис. 2.8). Касательное напряжение может иметь любое направление в плоскости сечения. Для удобства Очевидно, что полное напряжение можно выразить через
Полное напряжение не считается удобной мерой интенсивности внутренних усилий, так как материалы по разному сопротивляются действию нормальных и касательных напряжений. Нормальные напряжения (рис. 2.8) стремятся сблизить либо удалить отдельные части тела. Действие касательных напряжений (рис. 2.9) приводит к сдвигу одних частиц относительно других в плоскости сечения.
Если мысленно вырезать вокруг какой-нибудь точки тела элемент в виде бесконечно малого кубика, то по его граням в общем случае будут действовать напряжения, представленные на рис. 2.10. Совокупность напряжений на всех элементарных площадках, проведённых через какую – либо точку тела, называется напряжённым состоянием в данной точке.
Если по граням кубика действуют только нормальные напряжения, то они называются главными, а площадки, на которых они действуют, – главными площадками. Можно доказать, что в каждой точке напряжённого тела существует три главные взаимно перпендикулярные площадки. Главные напряжения обозначают
Зная напряжённое состояние в любой точке тела, можно оценить его прочность. В простейших случаях оценка прочности детали производится по наибольшему нормальному либо по наибольшему касательному напряжению.
Условие прочности в этих случаях выразится неравенствами:
где [ В более сложных случаях оценка прочности производится по приведенному напряжению в соответствии с одной из теорий прочности.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рис. 2.1
Рис. 2.1
 Рис. 2.2
Рис. 2.2
 Рис. 2.3
Рис. 2.3
 Рис. 2.4
Рис. 2.4
 Рис. 2.5
Рис. 2.5
 ,
,  ,
,  ,
,  (рис. 2.6). Для определения внутренних сил, действующих в любом сечении, например n-n, мысленно рассечём тело по этому сечению и одну из частей отбросим (рис. 2.7). На оставшуюся часть тела действуют силы
(рис. 2.6). Для определения внутренних сил, действующих в любом сечении, например n-n, мысленно рассечём тело по этому сечению и одну из частей отбросим (рис. 2.7). На оставшуюся часть тела действуют силы  Рис. 2.6 Рис. 2.7
Рис. 2.6 Рис. 2.7
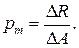
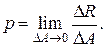
 представляют в виде двух составляющих по направлению координатных осей (рис. 2.9). У нормального напряжения ставится индекс, указывающий, какой из осей параллельно это напряжение. Растягивающие нормальные напряжения принято считать положительными, сжимающие – отрицательными. Касательные напряжения снабжены двумя индексами. Первый показывает, какой оси параллельна нормаль к площадке действия данного напряжения; второй – какой оси параллельно само напряжение.
представляют в виде двух составляющих по направлению координатных осей (рис. 2.9). У нормального напряжения ставится индекс, указывающий, какой из осей параллельно это напряжение. Растягивающие нормальные напряжения принято считать положительными, сжимающие – отрицательными. Касательные напряжения снабжены двумя индексами. Первый показывает, какой оси параллельна нормаль к площадке действия данного напряжения; второй – какой оси параллельно само напряжение. и
и 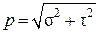
 Рис. 2.8 Рис. 2.9
Рис. 2.8 Рис. 2.9
 ,
,  ,
,  , при этом с учётом знака напряжения
, при этом с учётом знака напряжения  , (рис. 2.11). Различные виды напряжённого состояния классифицируются в зависимости от числа возникающих главных напряжений. Если отличны от нуля все три главных напряжения, то напряжённое состояние называется трёхосным или объёмным. 1Если равно нулю одно из главных напряжений, то напряжённое состояние называется двухосным или плоским. Если равны нулю два главных напряжения, то напряжённое состояние одноосное или линейное.
, (рис. 2.11). Различные виды напряжённого состояния классифицируются в зависимости от числа возникающих главных напряжений. Если отличны от нуля все три главных напряжения, то напряжённое состояние называется трёхосным или объёмным. 1Если равно нулю одно из главных напряжений, то напряжённое состояние называется двухосным или плоским. Если равны нулю два главных напряжения, то напряжённое состояние одноосное или линейное. Рис. 2.10 Рис. 2.11
Рис. 2.10 Рис. 2.11