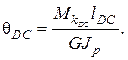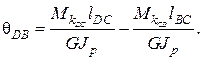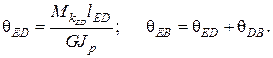|
|
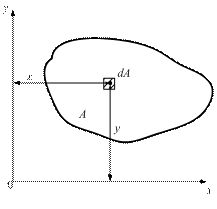
Геометрические характеристики плоских сечений2.9.1. Статические моменты плоских сечений При изучении вопросов прочности, жёсткости и устойчивости необходимо уметь определять некоторые геометрические характеристики сечений, к которым относятся статические моменты, моменты инерции и моменты сопротивления. Статическим моментом площади фигуры относительно оси х (рис. 2.24), взятой в той же плоскости, называется сумма произведений элементарных площадок dA фигуры на их расстоянии до оси. Перейдя от суммы к интегралу, выразим статический момент относительно оси х:
Рис. 2.24
Статический момент относительно оси у можно записать в виде
Рассматривая элементарную площадку как силу, а расстояние её от оси – как плечо силы, на основании теоремы Вариньона (сумма моментов составляющих равна моменту равнодействующей) можно записать:
где xc и yc – координаты центра тяжести всей площади А относительно осей x и y. Следовательно, статический момент плоской фигуры относительно какой–либо оси равен произведению всей площади на расстояние её центра тяжести от этой оси. Если x и y проходят через центр тяжести фигуры, то статический момент относительно этих осей равен нулю. Такие оси называются центральными. Размерность статического момента – метр кубический (м3); он может быть как величиной положительной, так и отрицательной. Если сложная фигура может быть разбита на простые, площади и центры тяжести которых легко определяются (прямоугольники, треугольники, круги), то статический момент всей фигуры относительно какой-либо оси может быть определён как сумма статических моментов отдельных её частей относительно той же оси:
где Sx – статический момент всей фигуры; Обозначим площади отдельных частей фигуры через
(2.33)
откуда расстояние центра тяжести всей фигуры от оси х определяется формулой:
Аналогично вторую координату центра тяжести всей фигуры определим по формуле:
2.9.2. Моменты инерции плоских сечений
Полярным моментом инерции сечения Jp называется сумма произведений элементарных площадок (dA) на квадраты их расстояний (ρ2) до какого-либо полюса, лежащего в плоскости сечения, распространённая на всю площадь сечения (см. рис. 2.25):
Рис. 2.25 Осевым моментом инерции площади сечения относительно какой-либо оси, лежащей в её плоскости, называется сумма произведений элементарных площадок на квадраты расстояний их до этой оси:
Из рис. 2.25 видно, что ρ2=x2+y2. Подставим это выражение в формулу (2.36) и получим:
Следовательно, сумма осевых моментов инерции плоского сечения относительно двух перпендикулярных осей равна полярному моменту инерции относительно полюса, представляющего точку пересечения этих осей. Осевые и полярные моменты инерции измеряются в метрах в четвертой степени (м4). Они всегда положительны и не могут быть равны нулю.
2.9.3. Моменты инерции простых плоских сечений Определим моменты инерции наиболее распространенных плоских сечений. · Прямоугольник (рис. 2.26). Вычислим момент инерции сечения относительно оси х, проходящей через центр тяжести параллельно основанию. Выделим на расстоянии у от оси х бесконечно узкую площадку высотой dy, тогда dA=b dy. В соответствии с формулой (2.37):
Аналогично находим осевой момент инерции относительно оси у:
Для квадратного сечения со стороной а:
· Круг радиуса r (рис. 2.27). Определим вначале полярный момент инерции относительно центра круга. За dA примем площадь бесконечно тонкого кольца толщиной dρ и радиусом ρ, тогда dA=2πρdρ. Подставим это значение в формулу (2.36):
Определим теперь осевые моменты инерции. Согласно формуле (2.38) для круглого сечения Jp=2Jx=2Jy следовательно:
· Кольцо (рис. 2.28). Воспользуемся формулой (2.42), приняв пределы интегрирования от R до r.
Рис. 2.27 Рис. 2.28
Обозначим отношение d/D=α. Тогда:
Аналогично сплошному сечению определим осевой момент инерции кольца:
2.9.5. Зависимость между моментами инерции относительно параллельных осей, одна из которых центральная Момент инерции сложной фигуры равен сумме моментов её составных частей:
где Выражение (2.47) следует из свойства определённого интеграла
где А – площадь всей фигуры; A1,A2,A3,…An – площади каждой части фигуры. Таким образом, для вычисления момента инерции сложного поперечного сечения его необходимо разбить на ряд простых фигур, вычислить момент инерции относительно оси каждой фигуры и затем все моменты инерции просуммировать. Для определения осевого момента инерции сложного по конфигурации поперечного сечения необходимо иметь формулу перехода для моментов инерции при параллельном переносе оси. Оси, проходящие через центр тяжести фигуры, называются центральными осями, а момент инерции, определённый относительно центральной оси, называется центральным моментом инерции. Положим, что х – центральная ось, момент инерции относительно которой Jx нам известен. Определим момент инерции
Рис. 2.30
Расстояния всех элементарных площадок dA от оси x1 будет больше на постоянную величину а, т. е. y1 = y+a.
Первый интеграл представляет собой центральный момент инерции. Второй интеграл равен нулю, так как это статический момент площади фигуры относительно оси, проходящей через центр тяжести с. Третий интеграл равен а2·A. Следовательно,
Формула (2.48) широко применяется в практике и читается следующим образом: момент инерции сечения относительно какой–либо оси равен сумме момента инерции относительно центральной оси, ей параллельной, и произведению площади всего сечения на квадрат расстояния между осями. Отметим, что моменты инерции прокатных сечений (двутавров, швеллеров, уголков и др.) приведены в таблицах сортамента.
Сдвиг и кручение 2.10.1 Определение напряжений и деформаций при сдвиге
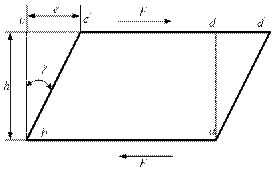
Если на брус действуют перпендикулярно его оси две равные по модулю силы F, направленные в противоположные стороны и имеющие небольшое расстояние между линиями их действия, то при достаточной величине этих сил происходит срез (см. рис. 2.31). Две части бруса отделяются одна от другой по линии n – n. Характерным для среза является близость расположения сил F, как это бывает у ножниц при разрезании, например, листа металла. Деформация, которая предшествует срезу, называется сдвигом. Эта деформация заключается в изменении прямых углов элементарного прямоугольника abcd, который после сдвига трансформируется в параллелепипед abc'd' (см. рис. 2.32). Рассмотрим элемент бруса abcd до и после сдвига (рис. 2.33). Величина сс`, на которую сдвинулось сечение cd относительно сечения ab, расположенного от него очень близко, называется абсолютным сдвигом. Абсолютный сдвиг зависит от расстояния h между смежными сечениями ab и cd.
Рис. 2.33
Угол γ, на который изменяются прямые углы прямоугольника, называется относительным сдвигом. Относительный сдвиг определим из соотношения:
Функцию tg γ приравняем к аргументу ввиду того, что в упругом состоянии, которое рассматриваем, угол γ очень мал. Таким образом, за меру сдвига принимают относительный сдвиг γ, т. е. отношение абсолютного сдвига между двумя близко расположенными смежными сечениями к расстоянию между этими сечениями. Единица измерения относительного сдвига – радиан. Рассечём брус по линии n – n между перерезывающими силами F (рис. 2.31) и, применив метод сечений, заменим действие отброшенной части на оставшуюся внутренними силами (рис. 2.34). Эти силы действуют в плоскости
Рис. 2.34
сечения, следовательно, сдвиг вызывает касательные напряжения. Если предположить, что внутренние силы распределяются равномерно по площади сечения, то касательные напряжения определяются формулой:
где А – площадь поперечного сечения бруса. Экспериментально установлено, что величина сдвига в пределах упругих деформаций пропорциональна сдвигающей силе F, расстоянию между плоскостями сдвига h и обратно пропорциональна площади поперечного сечения А, т. е.:
где GA – жёсткость сечения бруса при сдвиге. Учитывая выражения (2.49) и (2.50), из уравнения (2.51) найдём:
Формула (2.52) выражает закон Гука при сдвиге: угловые деформации пропорциональны касательным напряжениям. Величина G зависит от свойств материала и называется модулем упругости сдвига. Между модулями упругости и сдвига существует зависимость:
где μ – коэффициент поперечной деформации. В практических расчётах принимают для одного и того же материала G=0,4E. Модуль сдвига G = 8·104МПадля стали.
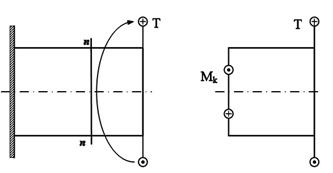
2.10.2. Определение внутренних силовых факторов при кручении Кручением называется такой вид деформации, при которой в поперечных сечениях стержня действуют только крутящие моменты, а остальные силовые факторы (нормальная и поперечная силы и изгибающий момент) отсутствуют. Эти крутящие моменты Mk возникают под действием внешних моментов Т, которые передаются на вал в местах посадки зубчатых колёс, шкивов и т.д. (рис. 2.35). Поперечная нагрузка также вызывает крутящие моменты, добавляя при этом поперечные и изгибающие силы (рис. 2.36).
Вращающиеся и работающие на кручение стержни, имеющие, как правило, круглое сечение, называются валами. Для определения напряжений и деформаций вала необходимо знать значения крутящих моментов, действующих на его отдельных участках. Условимся внешние моменты изображать в виде линии с двумя кружками, в которых будет поставлена точка (движение на нас) либо крестик (движение от нас). Для определения крутящих моментов Mk возникающих в сечениях вала под действием внешних скручивающих моментов Т или поперечных сил F1, применим метод сечений. Мысленно рассечём вал на две части, левую отбрасываем и рассматриваем равновесие оставшейся правой части (см. рис. 2.37). Действие отброшенной части заменяем крутящим моментом Mk. Для равновесия отсечённой части необходимо, чтобы алгебраическая сумма всех моментов, действующих на неё, была равна нулю. Отсюда в рассматриваемом сечении n–n внутренний крутящий момент Mk равен внешнему Т.
Рис. 2.37
Если на отсечённую часть будут действовать несколько внешних моментов, то, рассуждая аналогичным образом, делаем вывод, что крутящий момент в сечении численно равен алгебраической сумме внешних моментов, действующих по одну сторону от сечения:
Диаграмма, показывающая распределение значений крутящих моментов по длине вала, называется эпюрой крутящих моментов. Для построения эпюр необходимо условиться о правиле знаков крутящих моментов на эпюре. Вообще говоря, физического смысла знак крутящего момента не имеет, важно лишь принятое правило выдержать по всей длине вала. Крутящий момент в сечении n-n будем считать положительным, когда внешний момент Т вращает отсечённую часть против часовой стрелки, если смотреть на отсечённую часть со стороны сечения. Если внешний момент вращает отсечённую часть по часовой стрелке при взгляде со стороны сечения, то крутящий момент в сечении будем считать отрицательным. Построение эпюры крутящих моментов поясним на следующем примере. Рассмотрим вал AF, вращающийся с постоянной угловой скоростью ω в подшипниках К и N (см. рис. 2.38). Вал находится в равновесии под действием четырёх моментов, приложенных в сечениях B, C, D и E. Рассечём вал в любом месте на участке AB и, рассмотрев левую оставшуюся часть, определим, что на участке I крутящий момент в сечении равен нулю. Рассечём вал на участке II и определим, что
Рис. 2.38
Построенная эпюра имеет вид прямоугольников, в местах приложения внешних моментов ординаты эпюры скачкообразно изменяются на величину приложенного в этом сечении внешнего момента. Если на вал действуют поперечные силы, вызывающие кручение, то перед построением эпюр необходимо определить внешние моменты, создаваемые этими силами. Для схемы, изображённой на рис. 2.36, В практике чаще всего задаётся не внешний скручивающий момент, а передаваемая мощность Р и частота вращения n, при этом Р задаётся в киловаттах, а n – в оборотах в минуту. Так как P=Tω, то можно записать:
где размерность Т – [Нм]; размерность Р – [Вт] и ω– [рад/c]. Выразим угловую скорость ω через частоту вращения n:
Подставим мощность Р и ω из (2.55) в формулу (2.54):
Зависимость (2.56) широко используется в практических расчётах, т. к. позволяет определить крутящий момент в ньютонметрах, используя единицы измерения мощности и частоты вращения соответственно в киловаттах и оборотах в минуту. 2.10.3. Определение касательных напряжений и деформаций при кручении стержня круглого сечения Крутящие моменты представляют собой равнодействующие внутренних сил. При кручении стержня в его поперечных сечениях возникают непрерывно распределённые касательные напряжения, которые нужно уметь определять при расчётах на прочность. Нанесём на круглый стержень ортогональную сетку и нагрузим его внешним моментом Т (рис. 2.39). По результатам этого опыта можно сделать следующие выводы: · прямоугольники ортогональной сетки превратились в параллелограммы, следовательно, в поперечных сечениях действуют касательные напряжения; · расстояния между линиями, нормальными оси стержня, и длина всего стержня не изменились. Не изменился также и диаметр стержня. Можно предположить, что каждое поперечное сечение поворачивается в своей
Рис. 2.39
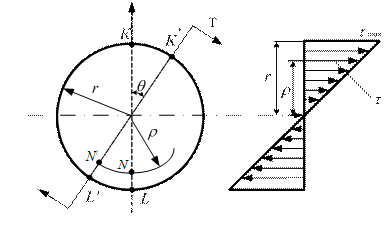
плоскости на некоторый угол, оставаясь плоским и нормальным к оси (гипотеза Бернулли). На основании этой гипотезы делаем вывод о том, что радиусы всех поперечных сечений повернулись на определённые углы, оставаясь прямолинейными. Таким образом, точка К переместится в положение К´ по дуге радиуса r, а точка N – в N` по дуге меньшего радиуса ρ (рис. 2.40, а). На основании этого можно сделать вывод, что при кручении круглого стержня в его поперечных сечениях действуют только касательные напряжения, а нормальные напряжения отсутствуют, т.е. мы имеем случай чистого сдвига.
а б
Рис. 2.40
Для того чтобы установить закон распределения касательных напряжений по поперечному сечению круглого стержня, нагруженного крутящим моментом Т, рассмотрим его деформацию между сечениями I и II (см. рис. 2.39 и рис. 2.41). Угол сдвига элемента ABCD, расположенного на поверхности стержня:
Рис. 2.41
Угол сдвига элемента, расположенного на расстоянии
На основании закона Гука для сдвига можно записать
Из формулы (2.58) следует, что при кручении касательные напряжения τ и деформации γ прямо пропорциональны расстоянию от центра тяжести сечения. В центре тяжести круглого сечения касательные напряжения равны нулю, наибольшее значение они принимают на поверхности стержня. Эпюра касательных напряжений в поперечном сечении круглого стержня изображена на рис. 2.40, б. Определим касательные напряжения из условия, что крутящий момент в сечении представляет собой равнодействующий момент от касательных напряжений (рис. 2.42):
Рис. 2.42
где τdA – элементарная сила, действующая на площадке dA. Подставим в (2.59) касательные напряжения из формулы (2.58):
Интеграл
Подставим значение dΘ/dz в формулу (2.58) и получим:
Из (2.62) следует, что в точках, равноудалённых от центра сечения, касательные напряжения одинаковы. Наибольшие напряжения τ возникают в точках, расположенных на поверхности стержня, где ρ=r.
где величина Wp, представляющая геометрическую характеристику плоского сечения, носит название полярного момента сопротивления или момента сопротивления при кручении:
Для круглого сплошного сечения:
Для кольцевого сечения (рис. 2.28):
где α=d/D. Запишем условие статической прочности при кручении, обозначив допускаемое касательное напряжение через [τ]:
Величину [τ] принимают равной 0,5 – 0,6 допускаемого напряжения на растяжение. Уравнение (2.67) можно использовать только для круглых валов, как сплошных, так и полых; для валов других сечений его применять нельзя. Используя условие прочности, можно рассчитать диаметр вала либо определить максимальный допускаемый крутящий момент, который может передать вал. Подставим в формулу (2.67) выражение полярного момента сопротивления:
откуда:
Аналогично для полых валов можно записать:
Допускаемый из условия статической прочности при кручении максимальный крутящий момент определяют по формуле:
Определение деформаций при кручении стержня круглого сечения Для определения деформаций вала при кручении воспользуемся формулой (2.61):
Взаимный угол поворота сечений на длине dz равен:
где GJp – жёсткость вала при кручении. Если крутящий момент и жёсткость не изменяются на всём участке интегрирования, то полную деформацию участка вала длиной ℓ можно определить по формуле:
Эта формула по структуре аналогична формуле для определения деформации при растяжении и сжатии. Угол закручивания, приходящийся на единицу длины вала, называется относительным углом закручивания:
На практике, кроме требований прочности, часто вводится условие жёсткости, которое заключается в том, что относительный угол закручивания не должен превышать определённую величину, т. е.
Формула (2.76) выражает условие жёсткости. В ней относительный и допускаемый угол закручивания на длине 1 м [φ] имеют размерность – радиан. В практике [φ] часто задают в градусах. В этом случае формулу (2.76) можно записать в виде:
Отметим, что для валов средних диаметров рекомендуют выбирать [φ0] равным 0,50 на один метр длины. Из выражения (2.77) можно определить диаметр вала по заданной жёсткости, учитывая, что полярный момент инерции
Для полого вала формула расчёта диаметра из условия жёсткости:
Используя формулу (2.74), можно построить эпюру угловых перемещений поперечных сечений вала, нагруженного крутящими моментами. Если рассматривается вращающийся вал, у которого нет неподвижных сечений, то для построения эпюры углов закручивания одно из сечений необходимо принять за условно неподвижное. Примем следующее правило знаков для углов поворота сечений: углы Построение эпюры углов закручивания рассмотрим на примере вращающегося вала, нагруженного четырьмя внешними моментами. Построим эпюру крутящих моментов и примем сечение B за условно неподвижное (рис. 2.43). Угол поворота на участке AB равен нулю, так как на этом участке отсутствует крутящий момент. Сечение C относительно B повернётся на угол
где
В принятом масштабе [град/м] отложим ординату
Угол поворота сечения D относительно сечения B, принятого за неподвижное, определяем как алгебраическую сумму углов D относительно C и C относительно B:
Аналогично определяем угол закручивания сечения E относительно D и затем E относительно B:
На участке EK поворота сечений не происходит, так как крутящий момент на этом участке равен нулю. Все сечения данного участка поворачиваются относительно сечения B на такой же угол, на какой повернулось относительно B сечение E. Участок эпюры здесь будет в виде прямой линии PR, параллельной оси вала.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
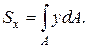 (2.29)
(2.29) (2.30)
(2.30) (2.31)
(2.31) (2.32)
(2.32) – статические моменты отдельных частей фигуры.
– статические моменты отдельных частей фигуры.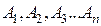 , а расстояния их центров тяжести от оси х – через
, а расстояния их центров тяжести от оси х – через  . Запишем выражение (2.32) в следующем виде:
. Запишем выражение (2.32) в следующем виде: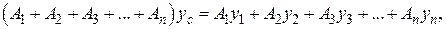
 (2.34)
(2.34) (2.35)
(2.35)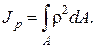 (2.36)
(2.36)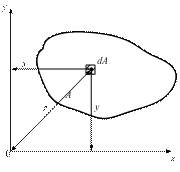
 (2.37)
(2.37) (2.38)
(2.38) Рис. 2.26
Рис. 2.26
 (2.39)
(2.39)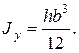 (2.40)
(2.40) (2.41)
(2.41) . (2.42)
. (2.42) (2.43)
(2.43)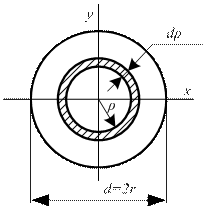
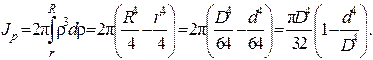
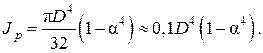 (2.44)
(2.44) (2.45)
(2.45) , (2.47)
, (2.47) – моменты инерции частей сложной фигуры относительно оси х.
– моменты инерции частей сложной фигуры относительно оси х.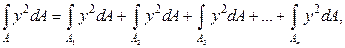
 фигуры относительно оси x1, параллельной центральной и отстоящей от неё на расстоянии а (см. рис. 2.30):
фигуры относительно оси x1, параллельной центральной и отстоящей от неё на расстоянии а (см. рис. 2.30):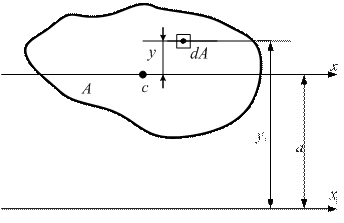
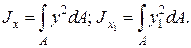
 .
.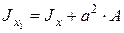 . (2.48)
. (2.48) Рис. 2.31 Рис. 2.32
Рис. 2.31 Рис. 2.32
 . (2.49)
. (2.49)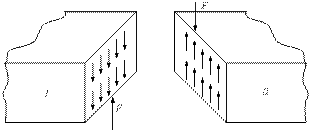
 , (2.50)
, (2.50)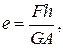 (2.51)
(2.51) (2.52)
(2.52) (2.53)
(2.53) Рис. 2.35 Рис. 2.36
Рис. 2.35 Рис. 2.36
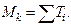
 Момент на участке BC в соответствии с правилом знаков считаем положительным. Рассмотрим сечение с-с на участке СD, отбросив правую часть. Крутящий момент в сечении
Момент на участке BC в соответствии с правилом знаков считаем положительным. Рассмотрим сечение с-с на участке СD, отбросив правую часть. Крутящий момент в сечении 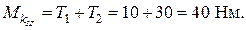 . Так как моменты Т1 и Т2 имеют одинаковое направление, момент в сечении определяется как их арифметическая сумма. Момент на IV участке определим как алгебраическую сумму внешних моментов, действующих на левую сторону от сечения d-d.
. Так как моменты Т1 и Т2 имеют одинаковое направление, момент в сечении определяется как их арифметическая сумма. Момент на IV участке определим как алгебраическую сумму внешних моментов, действующих на левую сторону от сечения d-d.  . Очевидно, что такой же результат получится и в случае, если отбросить левую часть вала и рассмотреть равновесие оставшейся правой. Отметим, что метод сечений не определяет, какую именно часть вала нужно отбрасывать, но для упрощения решения выгоднее отбросить ту часть, на которую действует большее число внешних силовых факторов (внешних моментов). Этот вывод справедлив для определения внутренних силовых факторов при любых видах деформаций. На последнем, пятом, участке крутящий момент равен нулю.
. Очевидно, что такой же результат получится и в случае, если отбросить левую часть вала и рассмотреть равновесие оставшейся правой. Отметим, что метод сечений не определяет, какую именно часть вала нужно отбрасывать, но для упрощения решения выгоднее отбросить ту часть, на которую действует большее число внешних силовых факторов (внешних моментов). Этот вывод справедлив для определения внутренних силовых факторов при любых видах деформаций. На последнем, пятом, участке крутящий момент равен нулю.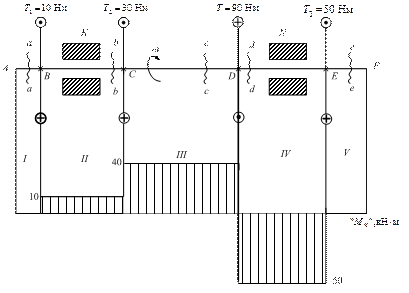
 .
. (2.54)
(2.54)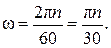 (2.55)
(2.55) . (2.56)
. (2.56)

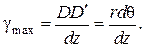
 от оси стержня:
от оси стержня: . (2.57)
. (2.57) . (2.58)
. (2.58)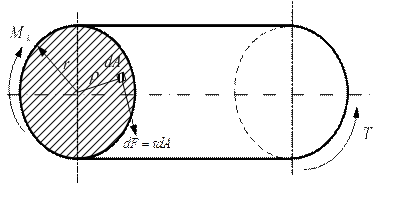
 (2.59)
(2.59) (2.60)
(2.60) представляет собой полярный момент инерции круглого сечения Jp , следовательно,
представляет собой полярный момент инерции круглого сечения Jp , следовательно,  , откуда:
, откуда: (2.61)
(2.61) (2.62)
(2.62) (2.63)
(2.63) (2.64)
(2.64)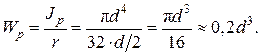 (2.65)
(2.65)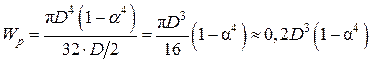 , (2.66)
, (2.66)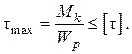 (2.67)
(2.67)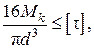 (2.68)
(2.68) (2.69)
(2.69) (2.70)
(2.70)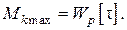 (2.71)
(2.71) (2.72)
(2.72)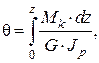 (2.73)
(2.73)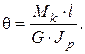 (2.74)
(2.74) (2.75)
(2.75) (2.76)
(2.76) (2.77)
(2.77)
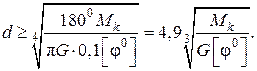 . (2.78)
. (2.78)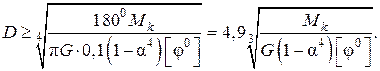 . (2.79)
. (2.79) будут считаться положительными, когда сечение, расположенное справа, поворачивается относительно сечения, расположенного слева, по часовой стрелке. При таком условии знак угла закручивания будет совпадать со знаком крутящего момента на участке вала.
будут считаться положительными, когда сечение, расположенное справа, поворачивается относительно сечения, расположенного слева, по часовой стрелке. При таком условии знак угла закручивания будет совпадать со знаком крутящего момента на участке вала.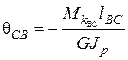 ,
, – крутящий момент на участке BC; ℓBC– длина участка BC.
– крутящий момент на участке BC; ℓBC– длина участка BC.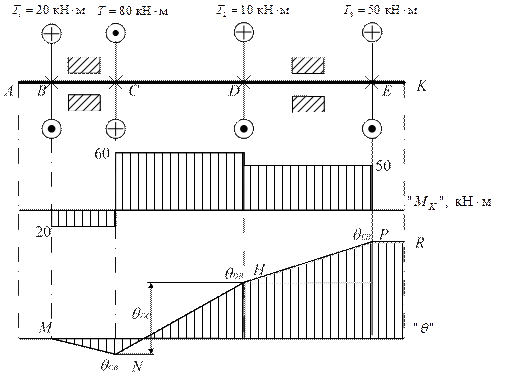 Рис. 2.43
Рис. 2.43