Теория метода и описание экспериментальной установки
Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты  , происходящих во взаимно перпендикулярных направлениях вдоль осей X и У. Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю: , происходящих во взаимно перпендикулярных направлениях вдоль осей X и У. Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю:
 (1) (1)
Разность фаз обоих колебаний равна 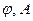 и и 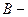 амплитуды складываемых колебаний. амплитуды складываемых колебаний.
Уравнение траектории результирующего колебания находится исключением из выражений (1) параметра 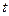 . Записывая складываемые колебания в виде . Записывая складываемые колебания в виде
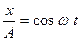 , ,
 . .
Заменяя во втором уравнении 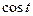 на на 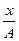 и и 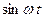 на на  получим после несложных преобразований уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно получим после несложных преобразований уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно
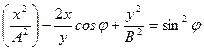 . (2) . (2)
Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.
Ориентация осей эллипса и его размеры зависят от амплитуд складываемых колебаний и разности фаз  . Рассмотрим некоторые частные случая, представляющие физический интерес: . Рассмотрим некоторые частные случая, представляющие физический интерес:
1.  . В данном случае эллипс вырождается в отрезок прямой . В данном случае эллипс вырождается в отрезок прямой
 , (3) , (3)
Где знак плюс соответствует нулю и четным значениям  (Рис.11а), а знак минус - нечетным значениям (Рис.11а), а знак минус - нечетным значениям  (рис.11б). Результирующее колебание является гармоническим колебанием с частотой (рис.11б). Результирующее колебание является гармоническим колебанием с частотой  и амплитудой и амплитудой 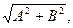 совершающимся вдоль прямой (3), составляющей с осью совершающимся вдоль прямой (3), составляющей с осью  угол угол  . В данном случае имеем дело с линейно - поляризованными колебаниями. . В данном случае имеем дело с линейно - поляризованными колебаниями.

Рисунок 11. График сложений колебаний при разности фаз  . .

Рисунок 12. График сложения колебаний при разности фаз  . .
2.   . В данном случае уравнение примет вид . В данном случае уравнение примет вид
 . (4) . (4) 
Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис 2). Кроме того, если 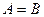 , то эллипс (4) вырождается в окружность. Такие колебания называются колебаниями, поляризованными по кругу. , то эллипс (4) вырождается в окружность. Такие колебания называются колебаниями, поляризованными по кругу.
В общем случае замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Форма этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний.
Физическая природа звуковых волн в газе и механизм их распространения в газе достаточно подробно изложены в работе 7. В бегущей звуковой волне смещения колебаний двух точек, находящихся на расстоянии друг от друга, сдвинуты по фазе на  . .
Отсюда  , а скорость звука в воздухе с учетом того, что , а скорость звука в воздухе с учетом того, что  определится выражением определится выражением
 (5) (5)
Формула (5) может быть использована для экспериментального определения скорости распространения звука в газе по измеренным значениям величин  . .
Для измерения скорости звука в воздухе служит установка, схема которой представлена на рисунке 13.

Рисунок 13. Схема экспериментальной установки для измерения скорости
звука в воздухе.
 Звуковые колебания в неподвижной трубе (1) возбуждаются телефоном (Т), закрепленном на конце подвижной грубы (2). Мембрана телефона приводится в движение переменным током звуковой частоты от звукового генератора (ЗГ). Звуковая волна достигает микрофона (М) и порождает в его цепи переменное напряжение, которое усиливается усилителем низкой частоты (УНЧ). Звуковые колебания в неподвижной трубе (1) возбуждаются телефоном (Т), закрепленном на конце подвижной грубы (2). Мембрана телефона приводится в движение переменным током звуковой частоты от звукового генератора (ЗГ). Звуковая волна достигает микрофона (М) и порождает в его цепи переменное напряжение, которое усиливается усилителем низкой частоты (УНЧ).
Между переменным напряжением на выходе звукового генератора и напряжением, возникающем в цепи микрофона, существует сдвиг по фазе  , зависящий от взаимного расположения микрофона и телефона. При перемещении подвижной трубы (2) с телефоном (Т) вдоль неподвижной трубы 1 на расстояние , зависящий от взаимного расположения микрофона и телефона. При перемещении подвижной трубы (2) с телефоном (Т) вдоль неподвижной трубы 1 на расстояние 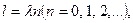 , составляющее целое число волн, разность фаз изменяется на , составляющее целое число волн, разность фаз изменяется на 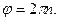 . Расстояние определяется при помощи измерительной линейки. Сдвиг фаз . Расстояние определяется при помощи измерительной линейки. Сдвиг фаз  можно определить по форме эллипса, описываемого на экране осциллографа (ЭО) электронным лучом, если вертикальные пластины X осциллографа соединить проводами (3) с выходом звукового генератора (ЗГ), а горизонтальные можно определить по форме эллипса, описываемого на экране осциллографа (ЭО) электронным лучом, если вертикальные пластины X осциллографа соединить проводами (3) с выходом звукового генератора (ЗГ), а горизонтальные  с микрофоном (М) через усилитель (УНЧ). Как было выяснено ранее (см. рис.11, а), при разности фаз с микрофоном (М) через усилитель (УНЧ). Как было выяснено ранее (см. рис.11, а), при разности фаз  эллипс вырождается в прямую, проходящую через первый и третий квадранты координатой плоскости, если эллипс вырождается в прямую, проходящую через первый и третий квадранты координатой плоскости, если  Подставляя принятую разность фаз Подставляя принятую разность фаз  в формулу (5), получим в формулу (5), получим
 (6) (6)
где 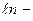 расстояние, соответствующее расстояние, соответствующее 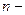 му числу повторения прямой на экране осциллографа му числу повторения прямой на экране осциллографа
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 .
.

 , происходящих во взаимно перпендикулярных направлениях вдоль осей X и У. Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю:
, происходящих во взаимно перпендикулярных направлениях вдоль осей X и У. Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю: (1)
(1)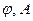 и
и 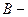 амплитуды складываемых колебаний.
амплитуды складываемых колебаний.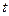 . Записывая складываемые колебания в виде
. Записывая складываемые колебания в виде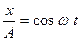 ,
, .
.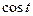 на
на 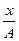 и
и 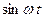 на
на  получим после несложных преобразований уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно
получим после несложных преобразований уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно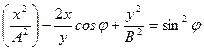 . (2)
. (2) . Рассмотрим некоторые частные случая, представляющие физический интерес:
. Рассмотрим некоторые частные случая, представляющие физический интерес: . В данном случае эллипс вырождается в отрезок прямой
. В данном случае эллипс вырождается в отрезок прямой , (3)
, (3) (Рис.11а), а знак минус - нечетным значениям
(Рис.11а), а знак минус - нечетным значениям 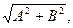 совершающимся вдоль прямой (3), составляющей с осью
совершающимся вдоль прямой (3), составляющей с осью  угол
угол  . В данном случае имеем дело с линейно - поляризованными колебаниями.
. В данном случае имеем дело с линейно - поляризованными колебаниями. .
.
 . В данном случае уравнение примет вид
. В данном случае уравнение примет вид . (4)
. (4) 
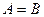 , то эллипс (4) вырождается в окружность. Такие колебания называются колебаниями, поляризованными по кругу.
, то эллипс (4) вырождается в окружность. Такие колебания называются колебаниями, поляризованными по кругу. .
. , а скорость звука в воздухе с учетом того, что
, а скорость звука в воздухе с учетом того, что  определится выражением
определится выражением (5)
(5) .
.
 Звуковые колебания в неподвижной трубе (1) возбуждаются телефоном (Т), закрепленном на конце подвижной грубы (2). Мембрана телефона приводится в движение переменным током звуковой частоты от звукового генератора (ЗГ). Звуковая волна достигает микрофона (М) и порождает в его цепи переменное напряжение, которое усиливается усилителем низкой частоты (УНЧ).
Звуковые колебания в неподвижной трубе (1) возбуждаются телефоном (Т), закрепленном на конце подвижной грубы (2). Мембрана телефона приводится в движение переменным током звуковой частоты от звукового генератора (ЗГ). Звуковая волна достигает микрофона (М) и порождает в его цепи переменное напряжение, которое усиливается усилителем низкой частоты (УНЧ).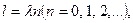 , составляющее целое число волн, разность фаз изменяется на
, составляющее целое число волн, разность фаз изменяется на 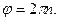 . Расстояние определяется при помощи измерительной линейки. Сдвиг фаз
. Расстояние определяется при помощи измерительной линейки. Сдвиг фаз  с микрофоном (М) через усилитель (УНЧ). Как было выяснено ранее (см. рис.11, а), при разности фаз
с микрофоном (М) через усилитель (УНЧ). Как было выяснено ранее (см. рис.11, а), при разности фаз  эллипс вырождается в прямую, проходящую через первый и третий квадранты координатой плоскости, если
эллипс вырождается в прямую, проходящую через первый и третий квадранты координатой плоскости, если  Подставляя принятую разность фаз
Подставляя принятую разность фаз  в формулу (5), получим
в формулу (5), получим (6)
(6)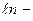 расстояние, соответствующее
расстояние, соответствующее 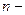 му числу повторения прямой на экране осциллографа
му числу повторения прямой на экране осциллографа