
|
|
Измерение и обработка их результатовМЕХАНИКА ЧАСТЬ I Учебно-методические указания к лабораторным работам по физике
Новосибирск 2016
УДК : 53(075)
Кафедра теоретической и прикладной физики
Составители: доц. И.М.Дзю; канд. техн. наук, доц. С.В.Викулов; канд. техн. наук, доц. В.Я. Чечуев; ст. преп. М.Г. Алешкевич
Рецензент д-р техн. наук, проф. кафедры «Физика» СГУПС П.М. Плетнев.
Механика. Часть I. Учебно-методические указания к лабораторным работам. /Новосиб. гос. аграр. ун-т, Инженерный. инст.; сост.: И.М. Дзю, С.В. Викулов, В.Я. Чечуев, М.Г. Алешкевич.; Новосибирск: Изд-во НГАУ. 2012. – 46с.
Учебно-методические указания по физике предназначены для обеспечения учебного процесса в физических лабораториях на дневном и заочном отделениях НГАУ. Указания охватывают весь цикл предлагаемых студентам лабораторных работ и являются достаточными для всех вариантов учебных планов по физике, практикуемых в НГАУ.
Утверждено и рекомендовано к изданию методическим советом Инженерного института, протокол № … от … 2016 г.
©Новосибирский государственный аграрный университет, 2012 1 . Содержание отчета 1.1. Назначение лабораторной работы и фамилия исполнителя. 1.2.Кратная формулировка цели лабораторной работы, включающая названия измеряемых физических величин и изучаемых физических законов. 1.3. Перечисление используемых в лабораторной работе приборов и принадлежностей. 1.4. Теоретическая часть лабораторной работы, включающая описание основных формул и законов физики, используемых в лабораторной работе. 1.5. Схемы размещения и соединения различных приборов и устройств. Включая общий вид всей установки. 1.6. Таблицы с результатами измерений и вычислений промежуточных и основных величин. 1.7. Расчеты искомых величин, но описанным ранее формулам. 1.8. Графики зависимостей одних физических величин от других. 1.9.Выводы о степени разумности и понимания полученных результатов, включая открытие новых закономерностей. 2. Обработка результатов измерений
2.1 Результаты измеренийи их ошибки
Учебный физический эксперимент проводится с целью изучения законов физики. В основе физического эксперимента лежат прямые или косвенные измерения. При прямых измерениях значение искомой величины находят непосредственно по шкале прямо показывающих приборов (линейка, секундомер, вольтметр и т.п.). При косвенных измерениях значение физической величины находят на основании известной зависимости (формулы) между ней и другими величинами, значение которых получаются в результате прямых измерении. Измерить физическую величину абсолютно точно невозможно, так как всякое измерение с помощью приборов сопровождается той или иной ошибкой или погрешностью, то есть отклонением результата, полученного на опыте, от истинного значения измеряемой величины. Все погрешности, получаемые при измерениях, подразделяют на систематические, случайные и промахи. Систематическими называются погрешности, которые изменяют результат измерений в одну определенную сторону (уменьшая или увеличивая результат) и на определенную величину. Они проявляются, когда в процессе измерения не учтены причины, односторонне влияющие на результат измерений. Например, при измерении сопротивления резисторов пренебрегли сопротивлением вспомогательных проводников или сместили нуль шкалы термометра. В лабораторных работах мы этой погрешностью обычно пренебрегаем. Случайные погрешности обусловлены причинами, искажающими результаты измерений не в определенную сторону, а беспорядочно, от случая к случаю, как в сторону завышения, так и в сторону занижения. Они появляются, например, из-за непостоянства измеряемой величины в процессе измерений (температуры, напряжения источников тока и т. п.). Промахи – это большие по величине погрешности, сильно искажающие результат измерения. Они могут являться следствием неправильной записи, неверного отсчета, непонимания шкалы измерений и т.п. Например, вместо отсчета на шкале «23» экспериментатор записал «28» или правильно записал «23 В», но не заметил, что шкала допускает значения измеренных величин в пределах от нуля до 100 мВ.
2.2. Требованияк заполнению таблицы При оформлении таблицы необходимо придерживаться следующих указаний: 2.2.1. Столбцы таблицы вверху должны быть озаглавлены и в них через запятую необходимо указать размерности физических величин. 2.2.2. Таблица заполняется только численными значениями величин. 2.2.3. Общий множитель (особенно множитель 10 в любой степени) чисел данного столбца можно вывести в заголовок столбца и поставить перед единицей измерения (например, 10 мА).
Построение графиков 2.3.1. График выполняют на линованной бумаге или в тетради в клетку. 2.3.2. Выбирают масштаб каждого деления таким образом, чтобы в пределах листа и выбранного для нанесения графика прямоугольника можно было указать максимальное и минимальное значение измеренной или вычисленной величины, наносимой на график. Кривые должны занимать практически все поле чертежа. Через каждые 20-40 мм наносят масштабные делания на координатных осях. Около этих меток проставляются значения данной физической величины, кратные 1, 2, 5, 10 и т.д. 2.3.3. Около каждой оси наносят обозначение физической величины и через запятую ее размерность, множитель 10 в любой степени, на который умножается физическая величина, может быть вынесен в обозначение оси. 2.3.4. Экспериментальные точки наносят в виде маленьких точек (или вертикальных линий в случае показа ошибок измерений). Затем с помощью линейки или лекала между экспериментальными точками проводят прямую или кривую таким образом, чтобы количество точек и расстояния до них как с одной, так с другой стороны били примерно одинаковыми.
«Эксперимент никого» не обманывает, Обманчивы наши суждения». Леонардо да Винчи ВВЕДЕНИЕ
Настоящие указания являются первой частью лабораторного практикума по физике. В его состав входят работы по механике, которые поставлены в физических лабораториях НГАУ. Лабораторно - практические занятия по физике позволят студентам, во - первых, познакомится с основными методами точных физических измерений и овладеть наиболее важными приборами, во-вторых, более подробно изучить некоторые явления и законы природы, для полного понимании которых одного лекционного материала по физике бывает недостаточно. Задачи второго рода гоже носят характер измерительных, хотя на первое место в них выступает не выполнение измерений, а изучение самого явления. Предварительное изучение работ является непременным условием их последующего выполнения в лабораториях. В целях повышения эффективности этой предварительной работы студентов описания лабораторных работ содержат достаточно полные теоретические введения и подробные указания по проведению опытов. Готовность студентов к выполнению лабораторных работ проверяется преподавателем. Не подготовленные студенты к выполнению работ не допускаются. Отчет по выполняемой работе составляется дома. В конце настоящих описаний приводится список литературы для самоподготовки.
Лабораторная работа № 1 Изучение законов кинематикии динамики поступательного движения на машине Атвуда Цель работы: 1. Экспериментально исследовать зависимость скорости от времени. 2. Экспериментально исследовать зависимость ускорения от силы тяжести груза. 3. Определить общую массу всей движущейся системы. Приборы ипринадлежности: машина Атвуда, электронный секундомер, ключ для замыкания цепи.
Теория метода и описаниеэкспериментальной установки Физика изучает законы движения частиц вещества и распространения поля, создаваемого этими частицами. Место нахождения каждой частицы, а любой момент времени фиксируется радиусом-вектором Компоненты Геометрическое место точек, которые занимает частица в различные моменты времени в процессе своего движения, называется ее траекторией. В классической и квантовой механике траектории, по определению являются непрерывными линиями, поэтому для них зачастую оказывается возможным ввести определение вектора скорости как производной по времени от радиус-вектора, который в начальный момент времени равен Движение частицы с постоянной скоростью называется равномерным движением. График зависимости скорости от времени в этом случае представляет собой прямую горизонтальную линию. Равномерное движение широко распространено в природе. Приблизительно равномерно движется Земля вокруг Солнца, что порождает регулярную смену времен года. Свет в пустоте или в любом однородном материале также распространяется равномерно. Равномерно движутся все тела, на которые не действуют силы (по первому закону Ньютона). Рассмотрим простейший пример равномерного движения по одной из координат
Решение этого уравнения позволяет найти координату
Для характеристики изменения скорости
который равен скорости изменения скорости или производной по времени В этом случае скорости (вдоль направления равноускоренного движения) от времени имеет следующий вид:
Из определения скорости при равноускоренном движении (вдоль некоторого направления) с постоянным ускорением
График зависимости Набор физических величин Сила является результатом взаимодействия вещества и поля. Вещество и поле непосредственно сами с собой никогда не взаимодействуют. Сила появляется только при наличии вещества, например, его массы, гравитационного поля, заряда и электрического поля. Наглядно это было показано Ньютоном, который открыл формулу для вектора силы тяжести:
Здесь сила В частности, Ньютон для определения
Здесь Связь между динамикой и кинематикой устанавливается с помощью постулата Декарта, который предложил связь между вектором импульса
Постулат Декарта
Ньютон открыл, что скорость изменения импульса
Уточним смысл записи второго закона Ньютона. Распространяющееся в пространстве со скоростью света В данной лабораторной работе нам представляется возможность проверить формулу равноускоренного падения груза в поле тяготения Земли, а также экспериментально проверить (или заново открыть для себя) выполнение второго закона Ньютона, теоретически им предсказанного. Экспериментальную проверку обсуждавшихся выше физических законов мы будем производить с помощью машины Атвуда, которая состоит из двух грузов – противовесов, связанных нитью через вращающийся блок массы При одинаковой массе
Здесь эффективная масса блока (для поступательного движения) в два раза отличается от фактической, так как блок участвует только во вращательном движении. Векторные обозначения в дальнейшем будем опускать, так как рассматриваемое нами движение является приближенно одномерным. Перегрузок массы
Рисунок 1. Схема экспериментальной установки. 1– платформа, на которой стоит машина Атвуда; 2 – вращающийся блок, жестко связанный с нитью, удерживающей груз; 3 – противовес без перегрузков; 4 – чашка, в которую падает противовес с перегрузками; 5 – принимающая площадка, электрически фиксирующая падающий груз; 6 – противовес, на верх которого кладутся перегрузки; 7 – перегрузки. которые обеспечивают движение механической системы; 8 – пассивная платформа для удержания противовеса без перегрузков.
Возьмем интеграл и, учитывая нулевое начальное значение импульса, получим
Согласно постулату Декарта:
Скорость всей системы при заданной её массе
Подставляя в последнюю формулу значение импульса
Обозначим через
Откуда В такой записи, очевидно, что движение является равноускоренным, так как ускорение Решение дифференциального уравнения для скорости позволяет найти изменение координаты
в процессе падения груза на подставку от начального положения Если мы экспериментально измерили время
При точном знании массы
Считая
После экспериментального определения ускорения
Измерения и обработка их результатов 1. Проверьте наличие всех приборов и принадлежностей, включая пластинки различной массы, два цилиндрических противовеса, секундомер и запишите перед табл.1 массу 2. Подготовьте из набора пластинок перегрузок общей массой 3. Поместите подготовленный перегрузок (набор пластинок) массы 4. Удерживая правый противовес рукой, нажмите верхнюю кнопку «Пуск» секундомера (для освобождения лески от закрепления магнитом) и установите дно противовеса на произвольно заданном расстоянии 5. Закрепите магнитом леску, удерживающего грузы, на любой выбранной вами высотой 6. Запишите значение 7. Установите правый верхний тумблер «Секундомер» в верхнее положение и нажмите кнопку «Установка нуля» отсчета времени на секундомере. 8. После установки начала отсчета времени на секундомере нажмите левую верхнюю кнопку «Пуск» на секундомере и наблюдайте падение противовеса в чашечку, в конце которого произойдет остановка секундомера в момент столкновения противовеса с чашечкой. 9. Отсчитайте по секундомеру и запишите в табл. 1 время 10. Повторите п. 2-9 с различными массами 11. Теперь преступайте к заполнению результатов вычислений в оставшиеся клетки соответствующих строчек табл. 1. Для этого вначале вычислите и запишите в таблицу ускорение 12. Вычислите и запишите в таблицу значение кинетической энергии 13.Вычислите и запишите в таблицу значение потенциальной энергии 14.Постройте на основе таблицы данных график зависимости ускорения 15.Постройте график зависимости ускорения, а от силы 16.Найдите по последнему графику экспериментальное значение массы
Таблица 1.– Результаты измерений и вычислений
Контрольные вопросы
1. Выведите второй закон Ньютона и решите задачу на вычисление силы. 2. Выведите формулу для мощности и решите задачу на вычисление тягового усилия трактора. 3. Вычислить ускорение при равномерном движении по прямой и по окружности. 4. Выведите формулу зависимости ускорения от силы при массе, линейно изменяющейся во времени. 5. Дайте определение равноускоренного и равномерного движения и выведите формулы для пути и скорости в этих случаях на примере падения тела в вязкой среде. 6. Дайте определение импульса, кинетической и потенциальной энергии и рассчитайте приближенно эти величины для различных движений вашего собственного тела. 7. Получите теоретическое значение массы движущейся системы М.
Лабораторная работа № 2
Измерение скоростипули методом баллистического маятника
Цель работы – научиться измерять скорость пули, методом баллистического маятника используя законы сохранения импульса и энергии. Приборы и принадлежности: баллистический маятник, пружинный пистолет, пули различной массы, измерительная линейка.
Теория метода и описание экспериментальной установки
Метод основан на применении законов сохранения импульса и энергии при решении реальной физической задачи соударения неупругих тел (удар). Абсолютно неупругий удар – столкновение неупругих тел, в результатекоторого тела объединяются, двигаясь дальше как единое целое. Баллистический маятник представляет собой частично заполненный пластилином цилиндр массой
Рисунок 2. Схема экспериментальной установки. 1- пружинный пистолет, 2 - пуля, 3 - стержень, 4- цилиндр с пластилином, 5 - линейная шкала прибора.
На основании закона сохранения импульса (количества движения) системы тел имеем:
где
Массы
Отклоняясь на угол
Таким образом, закон сохранения энергии можно записать:
где Высоту подъема системы можно определить из геометрии (рис.2). По теореме Пифагора из треугольника ОАС, следует
Отсюда Учитывая, что
где
Подставляя выражение (5) в (2), получаем формулу для определения скорости пули:
Измерение и обработка их результатов 1. Взвесьте пули и данные занесите в таблицу 2. 2. Вставьте в отверстие пистолета пулю 3. Зафиксируйте на измеренной линейке при помощи «всадника-указателя» исходное положение цилиндра маятника 4. Произведите выстрел, нажав на спусковую скобу, и зафиксируйте максимальное отклонение маятника 5. Определите максимальное смещение маятника от положения равновесия 6. Опыт повторите не менее трех раз. Найдите среднее значение 7. Подставьте значения 8. С пулями
Таблица 2.–Результаты измерений и вычислений
Контрольные вопросы
1. Какой удар называется упругим, неупругим? 2. Какие законы сохранения используют при расчете скоростей после взаимодействия при упругом и неупругом ударе? Почему? 3. На пули после выстрела действует внешняя сила - сила тяжести, на маятник с пулей действуют внешние силы - сила тяжести, сила реакции опоры в оси и сила трения в оси маятника. Таким образом, очевидно, что рассматриваемая система не является замкнутой. Объясните, на каком основании Вы используете законы сохранения импульса и энергии? 4. Выведите рабочую формулу (6).
Лабораторная работа № 3
Изучение законов динамики вращательного движения с помощью маятника Обербека
Цель работы: 1. Изучить основной закон динамики вращательного движения. 2. Исследовать зависимость момента инерции маятника от распределения грузиков относительно оси вращения. Приборы и принадлежности: крестообразный маятник Обербека, набор грузов, масштабная линейка, штангенциркуль, секундомер, весы.
Теория метода и описание экспериментальной установки
Вращательное движение твердого тела возникает при действии на него силы, обладающей моментом относительно оси вращения тела. Сила – величин векторная. Если вектор силы лежит в плоскости, перпендикулярной к оси вращения, то моментом силы будет являться векторная физическая величине определяемая векторным произведением радиуса-вектора
где Маятник Обербека (рис.3) представляет собой крестовину, которая образована четырьмя стержнями и имеет ось вращения, закрепленную в стене или на стойке в портативном варианте прибора. На ось насажана втулка с двумя шкивами разных диаметров
.
Рисунок 3. Схема экспериментальной установки.
Стержни ввинчены во втулку под прямыми углами друг к другу. На стержни надеваются одинаковые тела массами Изучим экспериментально основной закон динамики вращательного движения
где 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
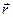 , начало которого совпадает с началом отсчета координат, а конец упирается в заданную частицу вещества.
, начало которого совпадает с началом отсчета координат, а конец упирается в заданную частицу вещества.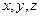 радиус-вектора
радиус-вектора  являются координатами частицы в выбранной нами системе отсчета координат. Например, при падение частицы с некоторой высоты координата изменяется от
являются координатами частицы в выбранной нами системе отсчета координат. Например, при падение частицы с некоторой высоты координата изменяется от 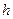 до нуля, а координаты
до нуля, а координаты  и
и 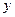 остаются при этом постоянными.
остаются при этом постоянными.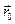 .
. . Тогда при известном постоянном значении скорости
. Тогда при известном постоянном значении скорости  :
: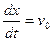 . (1)
. (1)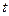 .
. . (2)
. (2) частицы используется вектор ускорения
частицы используется вектор ускорения , (3)
, (3)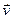 скорости. Движение с постоянным по величине ускорением
скорости. Движение с постоянным по величине ускорением 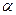 называется равноускоренным движением. График зависимости ускорения от времени представляет собой прямую горизонтальную линию.
называется равноускоренным движением. График зависимости ускорения от времени представляет собой прямую горизонтальную линию.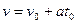 . (4)
. (4)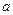 , начальной скорости
, начальной скорости  и начальной координатой
и начальной координатой  (5)
(5) задает кинематическое описание движения частиц без указания причин его вызывающих. Главной причиной изменения движения является сила. Изучение движений частиц под действием сил осуществляется в динамике.
задает кинематическое описание движения частиц без указания причин его вызывающих. Главной причиной изменения движения является сила. Изучение движений частиц под действием сил осуществляется в динамике. . (6)
. (6) – создается произведением массы
– создается произведением массы 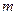 вещества на вектор
вещества на вектор  напряженности гравитационного поля. Динамическую величину
напряженности гравитационного поля. Динамическую величину  предложил использовать открытый им закон всемирного тяготения:
предложил использовать открытый им закон всемирного тяготения: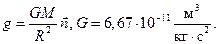 (7)
(7)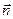 есть единичный вектор, направленный по расстоянию
есть единичный вектор, направленный по расстоянию 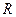 от точки приложения силы тяготения
от точки приложения силы тяготения 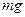 до начала координат, в котором находится центр масс
до начала координат, в котором находится центр масс 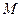 гравитирующего (притягивающего) тела.
гравитирующего (притягивающего) тела.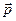 частицы вещества, ее инерционной массы
частицы вещества, ее инерционной массы 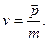 (8)
(8)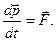 (9)
(9)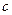 поле при взаимодействии с веществом создает в каждой точке своего места нахождения силу
поле при взаимодействии с веществом создает в каждой точке своего места нахождения силу 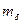 (рис 1).
(рис 1).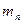 противовесов система находится в равновесии и неподвижна при расположении правого противовеса на любой высоте от приемной чашечки. Вся система приходит в движение после добавления к одному из противовесов перегрузка массой
противовесов система находится в равновесии и неподвижна при расположении правого противовеса на любой высоте от приемной чашечки. Вся система приходит в движение после добавления к одному из противовесов перегрузка массой  (10)
(10)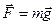 , под действием которой правый противовес начинает падать с высоты
, под действием которой правый противовес начинает падать с высоты  . (11)
. (11)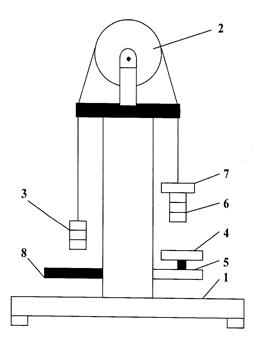
 . (12)
. (12) . (13)
. (13) . (14)
. (14)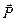 , получим значение
, получим значение 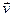 системы грузов машины Атвуда:
системы грузов машины Атвуда: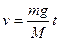 (15)
(15)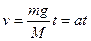 .
.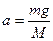 . (16)
. (16)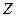 от времени
от времени 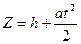 (17)
(17)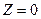 правого противовеса до конечного
правого противовеса до конечного  .
.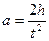 . (18)
. (18)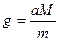 . (19)
. (19)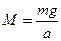 . (20)
. (20) всей системы:
всей системы: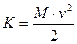 . (21)
. (21)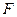 силы тяжести, создаваемой перегрузком.
силы тяжести, создаваемой перегрузком. всей изучаемой вами системы.
всей изучаемой вами системы.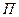 перегрузка в начале его падения.
перегрузка в начале его падения.

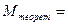
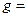

 кг
кг
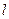 (рис.2) Вблизи маятника неподвижно закреплен пружинный пистолет, из которого стреляют в маятник пулями различной массы. При выстреле пуля со скоростью
(рис.2) Вблизи маятника неподвижно закреплен пружинный пистолет, из которого стреляют в маятник пулями различной массы. При выстреле пуля со скоростью  фиксируется на линейной шкале прибора.
фиксируется на линейной шкале прибора.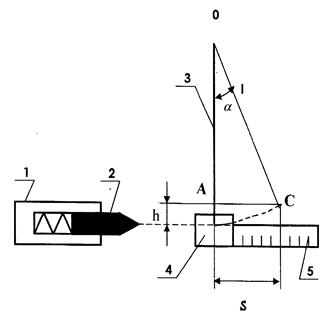
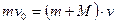 , (1)
, (1)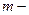 масса пули,
масса пули,  масса цилиндра,
масса цилиндра,  скорость пули перед ударом,
скорость пули перед ударом,  скорость цилиндра вместе с нулей после удара. Уравнение (1) дает возможность определить скорость пули:
скорость цилиндра вместе с нулей после удара. Уравнение (1) дает возможность определить скорость пули: . (2)
. (2) .
. не перейдет полностью в потенциальную:
не перейдет полностью в потенциальную:
 , (3)
, (3) ускорение свободного падения.
ускорение свободного падения.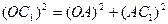 или
или 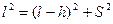
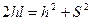 .
.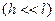 , получим:
, получим: , (4)
, (4)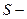 отклонение маятника от положения равновесия,
отклонение маятника от положения равновесия, 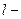 длина баллистического маятника. Решая (3) и (4) находим скорость пули:
длина баллистического маятника. Решая (3) и (4) находим скорость пули: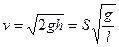 . (5)
. (5)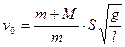 . (6)
. (6)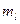 , и закрепите её пусковой скобой.
, и закрепите её пусковой скобой.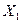 .
. .
.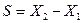 .
.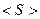 .
.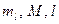 и
и 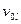 пули.
пули. и
и 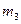 повторите действия пунктов 2 - 6 и рассчитайте их скорости. Результаты занесите в таблицу 2.
повторите действия пунктов 2 - 6 и рассчитайте их скорости. Результаты занесите в таблицу 2.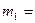
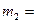
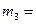
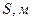

 , (1)
, (1)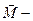 псевдовектор, по направлению совпадающий с поступательным движением правого винта при вращении его головки от
псевдовектор, по направлению совпадающий с поступательным движением правого винта при вращении его головки от 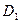 и
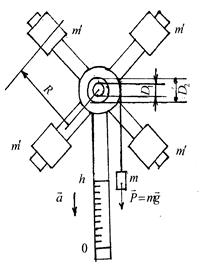
и  .
.
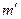 каждый, которые могут быть закреплены симметрично на расстоянии
каждый, которые могут быть закреплены симметрично на расстоянии  . Положение груза
. Положение груза 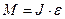 , (2)
, (2)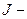 момент инерции маятника:
момент инерции маятника: 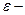 угловое ускорение.
угловое ускорение.